RNN(Recurrent Neural Network,순환 신경망)
시퀀스 데이터 이해하기
- 소리, 문자열, 주가 등의 데이터를 시퀀스(sequence)데이터로 분류한다.
- 시계열(time-series)데이터는 시간 순서에 따라 나열된 데이터로 시퀀스 데이터에 속한다.
- 시퀀스 데이터는 독립동등분포(i.i.d.)가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다. 즉, 여러 데이터가 순서와 관계없이 입력되던 것과는 다르게, 과거에 입력되던 데이터와 나중에 입력된 데이터 사이의 관계를 고려해야된다.
시퀀스 데이터를 어떻게 다루나요?
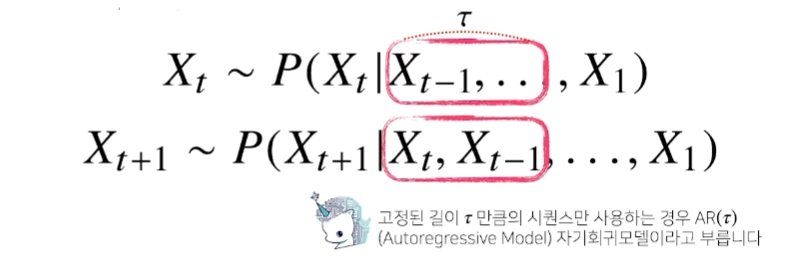
- 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 이용할 수 있다.
- 위의 조건부 확률은 과거의 모든 정보를 사용하지만 시퀀스 데이터를 분석할 때 모든 과거 정보가 필요한것은 아니다.
- 시퀀스 데이터를 다루기 위해서는 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요하다.
###RNN 이해하기
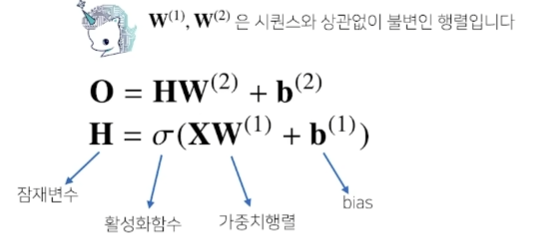
- 가장 기본적인 RNN 모형은 MLP와 유사한 모양이다.
- RNN은 이전 순서의 잠재변수와 현재의 입력을 활용하여 모델링한다.
- RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산한다.
BPTT(Backpropagation Through Time)
- BPTT를 통해 RNN의 가중치행렬의 미분을 계산해보면 아래와 같이 미분의 곱으로 이루어진 항이 계산된다.
기울기 소실의 해결책
- 시퀀스 길이가 길어지는 경우 BPTT를 통한 역전파 알고리즘의 계산이 불안정해지므로 길이를 끊는것이 필요하다. 이를 truncated BPTT라 부른다.
- 이런 기울기 소실의 문제로 길이가 긴 시퀀스를 처리하는데 문제가 있기 때문에 RNN을 사용하지 않고 요즘은 LSTM과 GRU를 사용한다.