결정트리 (Decision Tree)
참고
[ML] 결정트리(Decision Tree) - 기본구조와 CART, ID3 알고리즘
의사결정 나무 (Decision Tree) 기본 설명
결정 트리 학습법 - 위키백과, 우리 모두의 백과사전
결정 트리 학습법은 머신러닝 지도학습에서 가장 유용하게 사용되고 있는 기법 중 하나이다.
결정트리는 데이터에 있는 규칙을 통해 데이터셋을 분류/예측하는 지도학습(supervised) 모델이다.
- 결정 노드(Decision Node): 규칙 조건
- 리프 노드(Leaf Node/Terminal Node): 결정된 클래스의 값
- 서브 트리(Sub Tree): 새로운 규칙 조건마다 생성됨
목표 변수가 유한한 수의 값을 가지는 것을 분류트리라 하고,
결정 트리 중 목표 변수가 연속하는 값, 일반적으로 실수를 가지는 것은 회귀트리라 한다.

그렇다면 트리를 어떻게 쪼개나갈 것인가?
최대한 균일한(순도가 높은) 데이터 세트를 구성할 수 있도록 분할하는 것이 중요하다.
결정 노드는 정보 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙 조건을 만든다.
→ 이 판단을 불순도를 기준으로 한다.
→ 즉 가장 낮은 지니계수를 가진 피처가 결정트리에서의 루트 노드가 된다.
단점
의사결정 나무 알고리즘은 간단하면서 효과적인 알고리즘이지만, 과적합 (Overfitting)에 취약하다는 단점이 있다.
이러한 과적합을 막기 위해, 가지치기 (pruning) 과정을 수행 (사전 가지치기 (pre-pruning) & 사후 가지치기 (post-pruning))
- 나무의 최대 깊이 (depth)를 제한
- 자식 노드의 최소 샘플 수를 설정
- impurity/error 의 최소값을 설정
- impurity/error 변화값의 최소값을 설정
결정트리를 만드는데 여러 가지 알고리즘이 사용될 수 있다. 가장 대표적인 것은 CART 알고리즘과 ID3 알고리즘이다.
- CART(Classification and Regression Trees) - metric으로 Gini Index(Classification) 사용
- ID3(Iterative Dichotomiser 3) - metric으로 Entropy function과 information gain 사용
CART (Classification And Regression Tree) 알고리즘
- 불순도: Gini index Gini index는 엔트로피와 같은 불순도 (Impurity) 지표이다. Gini index는 엔트로피와 같이 분류가 잘 될 때 낮은 값을 갖습니다. 따라서 CART 알고리즘에서는 모든 조합에 대해 Gini index를 계산한 후, Gini index가 가장 낮은 지표를 찾아 분기합니다.
- Binary tree 가지 분기 시, 여러 개의 자식 노드가 아닌 단 두 개의 노드로 분기한다
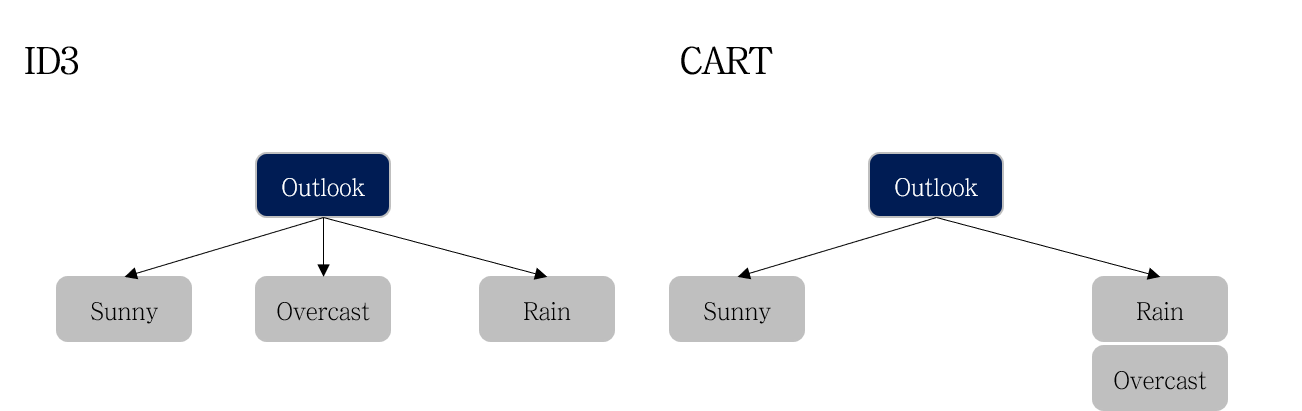 ID3 의 경우 모든 클래스 (e.g., Sunny, Overcast, Rain) 로 가지 생성 CART는 ‘하나의 클래스와 나머지’와 같이 가지가 생성
ID3 의 경우 모든 클래스 (e.g., Sunny, Overcast, Rain) 로 가지 생성 CART는 ‘하나의 클래스와 나머지’와 같이 가지가 생성
- Regression tree CART 알고리즘은 Regression(회귀)를 지원한다. 회귀 트리 (Regression Tree)를 사용 할 때는, 분기 지표를 선택할 때 사용하는 index를 불순도 (Entropy, Gini index)가 아닌, 실제값과 예측값의 오차를 사용한다.
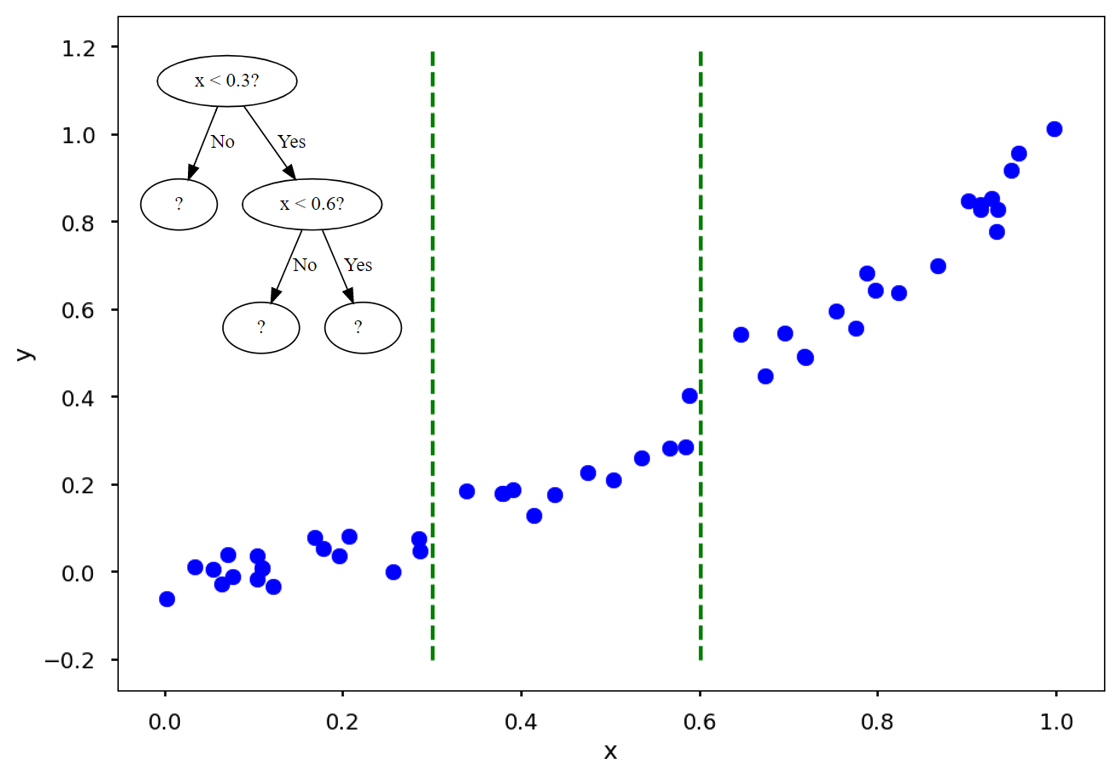
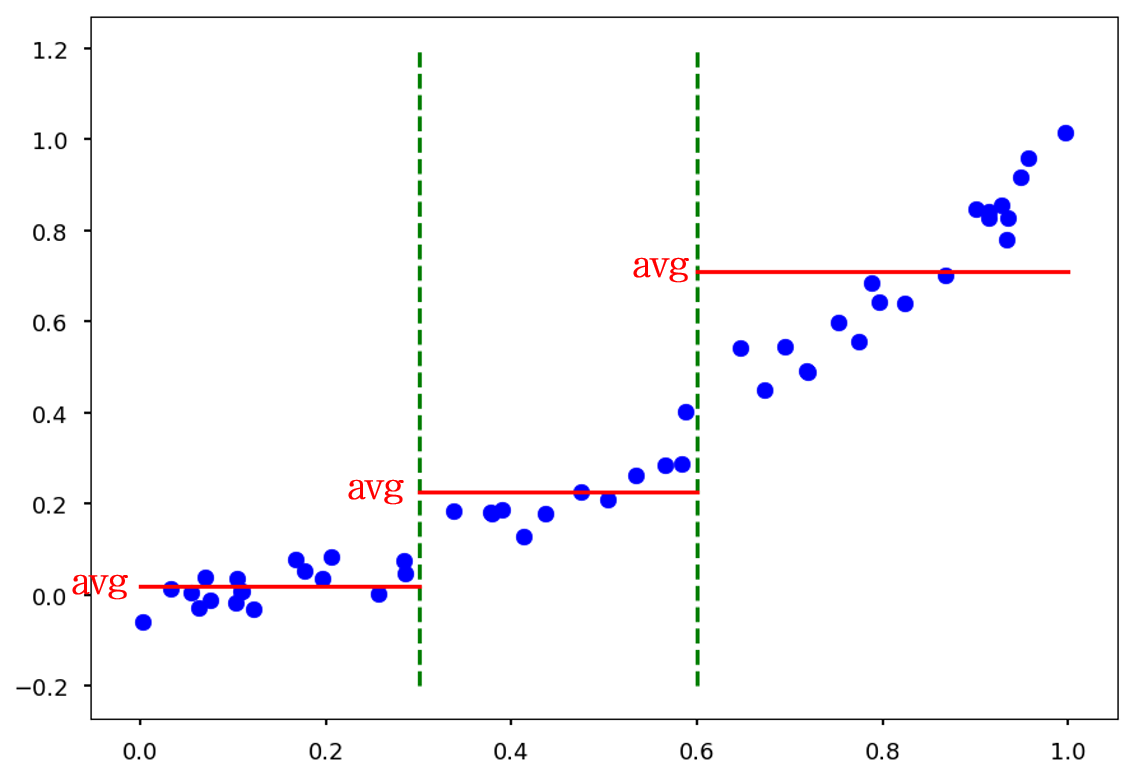
x<0.3 과 x<0.6 지표로 하고 x값이 들어올 경우, training data (파란 점)의 평균값 (빨간 실선)을 예측값으로 내놓습니다.
실제값과 예측값의 오차는 RSS나 MSE 와 같은 값으로 나타낸다.
