머신러닝 모델은 Loss 함수를 정의하고 그 Loss
함수를 최적화하게끔 만드는 것이 목적이다.

Loss는 $y$(실제값)와 $\hat{y}$(예측값)의 차이를 어떻게 정의하는가(measure하는가), 여기에는 여러 종류가 있다.

• Mean Squared Error Loss
• Cross Entropy Loss
• accuracity 등등

즉 머신러닝에서 러닝이란,
$y$(실제값)와 $\hat{y}$ (예측값)의 차이를 최소화하게끔 하는 최적의 모형을 찾아가는 과정이다.

loss function 이 없는 모델

• K-Nearest Neighbor
• Decision Tree

KNN 은 수학적으로 정의되는 Loss Function은 없지만 가까이 있는 이웃들의 Majority Voting을 하게되면 Loss를 최소화해 줄 수있다는 가정을 하는 것이다.

Decision Tree 도 수학적인 Loss 함수는 없지만 $y$와 예측되는 결괏값들의 차이를 최소화하는 목표는 동일하다.

Optimization (최적화)

예시)

• Neural Networks
  
  

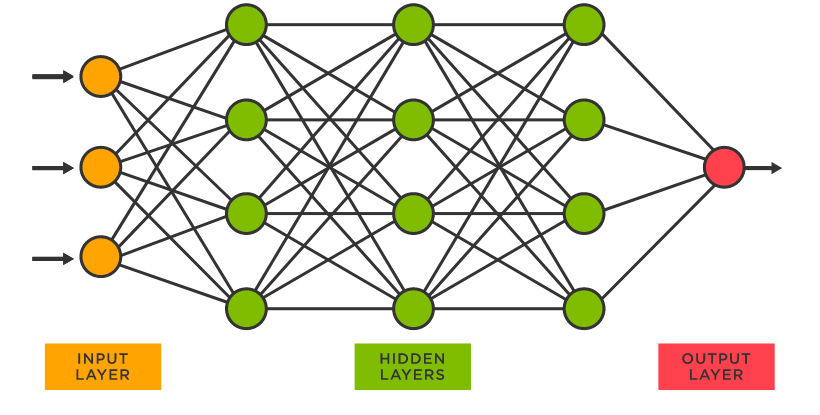
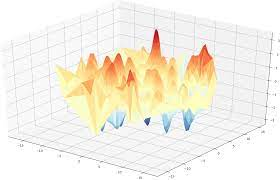
Neural Networks의 loss function은 엄청 복잡하고 고차원이라 단순 미분으로는 최적화를 찾을 수 없다.
-> 여러가지 방법의 최적화 기법이 있다!

Iterative Algorithm-based Optimization

• loss function 의 값을 줄이기 위해서 반복적으로 학습을 수행한다.

Gradient Descent (경사 하강법)

Gradient

참고
gradient 란?

Gradient란 다변수 함수의 모든 입력값에서 모든 방향에 대한 순간변화율이다. 함수의 최대 증가방향을 나타낸다.

Gradient 는 각 축 방향의 편미분의 합으로, 기울기가 가장 가파른 곳으로의 방향을 의미한다.

Gradient Descent

• Gradient Descent는 $-\nabla f$를 이용해서, 기울기가 가파르게 함숫값이 빠르게 작아지는 방향을 찾고 그 방향으로 한 발자국씩 계속 내려가는 방법이다.
• Gradient를 이용해서 함숫값을 줄인다고 해서 Gradient Descent라고 부른다.
• 함숫값을 가장 빠르게줄일 수 있는 방향으로 계속 내려간다.

Quadratic approximation

참고
Taylor series (테일러 급수)
Newton's Method

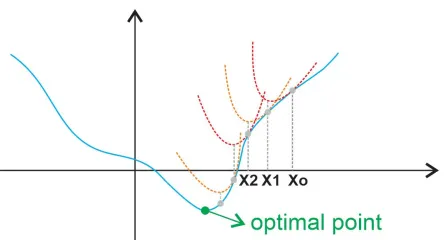
• 테일러 급수를 활용해, 잘 알지 못하는 다차원의 함수를 2차함수로 근사한다.
  • 복잡한 함수를 다루기 쉽고 이해하기 쉬운 다항함수로 대체
  • 복잡한 함수를 저차원의 다항함수로 근사하여 모델을 단순화
  • 2차함수는 미분값이 0인 지점을 찾기가 상대적으로 쉽다.

$W_c -t_c\nabla L$의미!!

현재 $W_c$에 있는데 함수를 작게 해 줄 수 있는
방향이 있고($-\nabla L$) 그 방향으로 $t_c$를 곱해서 이동시킨다.
$t_c$는 step size 를 말한다. (하이퍼파라메터임)
이 과정을 반복하다보면 approximation된 이차 함수의 가장 작은 점이 구해진다!

Gradient Descent 특징

• 극소나 극대점이 딱 하나 존재하는 그런 형태에서는 Gradient Descent를 적용해 주면 가장 좋은 해를 찾을 수 있다.
• 복잡한 형태 (미분해서 기울기가 0인 지점이 여러군데 인 형태), 극소나 극대점이 여러 군데 존재하고 있고 굴곡이 많은 그런 데이터 형태에 대해서는 가장 작은, 가장 좋은 값을 갖는 최적해 (Global Optimum)를 구한다고 보장 할 수는 없다.
• 그러나 지역적인 최소해만 잘 구하더라도 꽤 성능 좋은 모형이다.