참고
로지스틱 회귀와 시그모이드 함수 링크
로지스틱회귀 링크
로지스틱 회귀 위키백과 링크
Logistic Regression(로지스틱 회귀)이란?

Logistic Regression

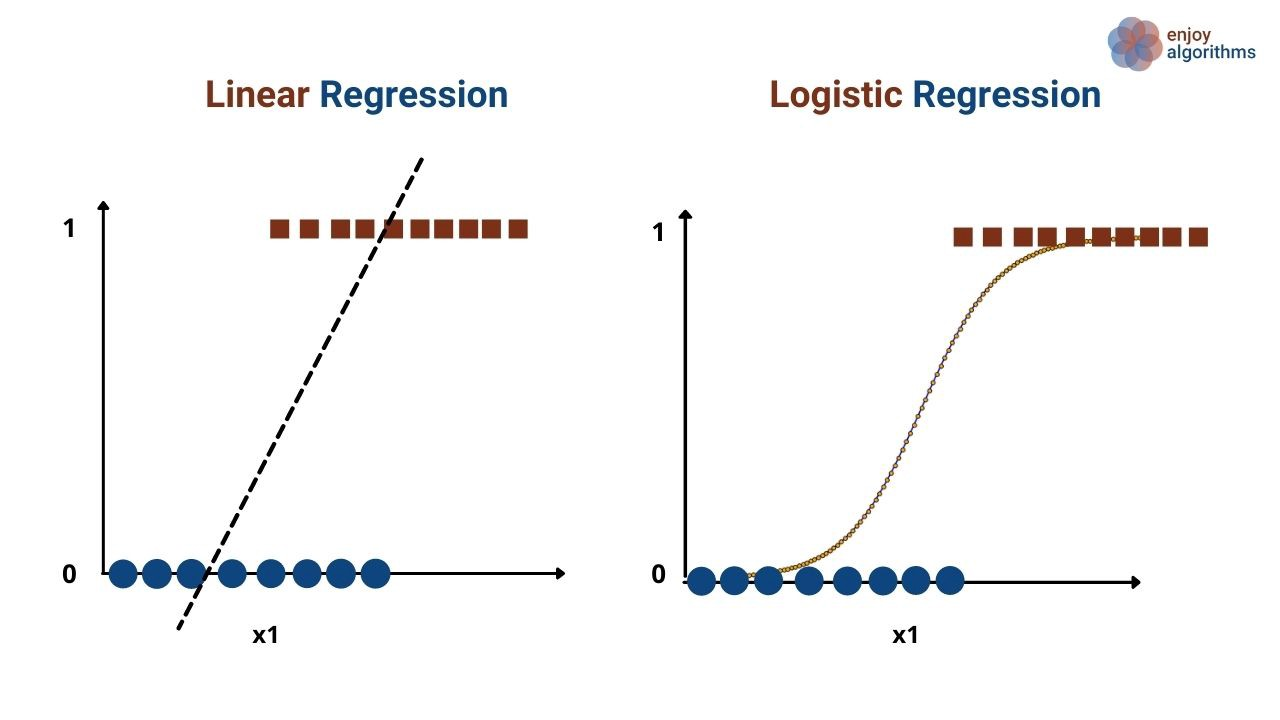
• 로지스틱 회귀는 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는 데 사용되는 통계 기법이다.

• 로지스틱 회귀의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것이다.

• 로지스틱 회귀는 독립 변수의 선형 결합으로 종속 변수를 설명한다는 관점에서는 선형 회귀 분석과 유사하나, 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하여 분류 모델이라고 볼 수 있다.

• 즉, 선형 모형을 사용하여 분류문제를 해결하는 알고리즘이다.

• 로지스틱 회귀는 종속변수가 이항형 문제(즉, 유효한 범주의 개수가 두개인 경우)를 지칭할 때 사용된다.

• 로지스틱 모형은 독립변수가 [-∞,∞]의 어느 숫자이든 상관없이 종속 변수 또는 결과 값이 항상 범위 [0,1] 사이에 있도록 한다.

• Logistic function이라는 변환 함수를 사용하기 때문에 Logistic Regression이라고 부른다.

  • 선형회귀는 직선을 가설로 사용하는 거고, 로지스틱 회귀는 시그모이드 함수를 가설로 사용하는거다!

Sigmoid Function (시그모이드 함수)

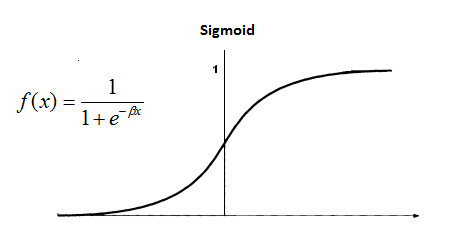
실제 많은 자연, 사회현상에서는 특정 변수에 대한 확률값이 선형이 아닌 S-커브 형태를 따르는 경우가 많다고 한다.
S-커브를 함수로 표현해낸 것이 바로 로지스틱 함수 즉 시그모이드 함수이다.
독립변수의 값(모든 실수)들을 받아서 0과 1 사이의 확률 값을 뱉어내는 수식이다.

• 시그모이드 함수를 사용한다면,
  • x의 값이 작을 때의 예측값은 1/(1+무한대) 으로 0 에 수렴할 것이며,
  • x의 값이 클 때의 예측값은 1/(1+0) 으로 1 에 수렴할 것이다.
  • 따라서, 예측 값을 0 과 1 사이의 값으로 추출할 수 있게 된다.

Cost Function (비용함수)

• Linear Regression 에서는 직선을 가설로 사용하고, mse를 비용함수로 사용한다.
• Rogistic Regression 은 가설로 시그모이드 함수를 사용하고, 비용함수로 Binary Cross Entropy 를 사용한다.

Log Odds

참고
로지스틱회귀(Logistic Regression) 쉽게 이해하기
로짓 변환(Logit Transform)
Logistic Function 링크

승산(Odds) = 성공 확률을 p로 정의할 때, 실패 대비 성공 확률 비율이다.
만약 0.7 확률로 시험에 합격한다고 하면, 떨어질 확률은 0.3 이므로 odds 는 이렇게 계산 할 수 있다.

로지스틱 회귀 모델에서(이진 분류일때)의 Odds는 다음과 같다.

sigmoid(x) : [0-1]
Odds : [0-$∞$]

Odds의 값이 양의 $∞$ 값을 갖는다. $log$를 취해준걸 로짓변환이라고 한다. (좌변과 우변의 값을 맞추기 위해서)

$β_1$의 해석 : x가 한단위 증가 했을 때 log(Odds)의 증가량