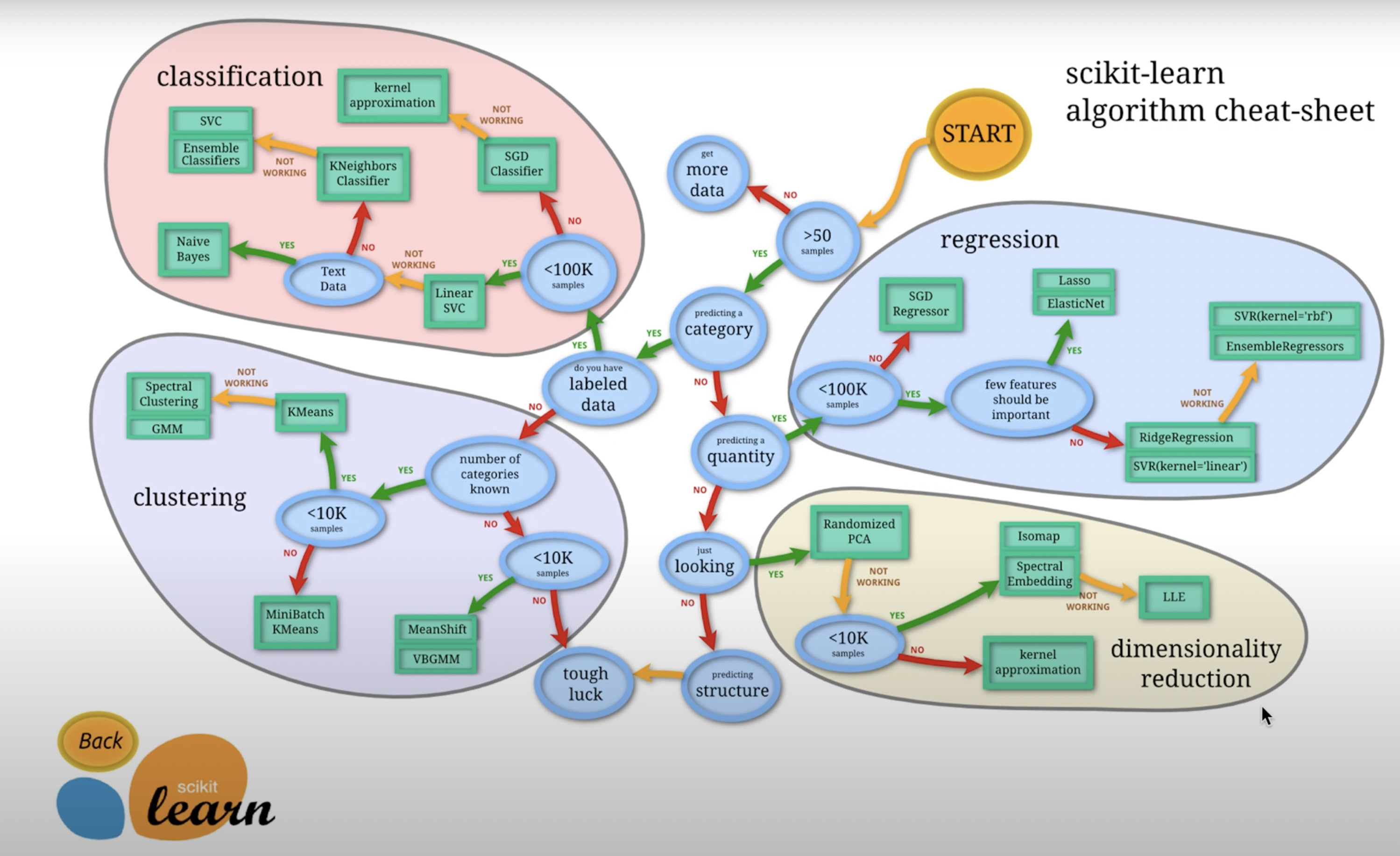
Supervised Learning
- 컴퓨터에게 입력과 출력을 주고, 입출력 간 관계를 학습하여 새로운 입력에 대해 적절한 출력을 내도록 하는 기계학습의 한 분야
- Input : feature(vector)
- Output : label
- 범주형 변수(classification), 연속형 변수(regression)
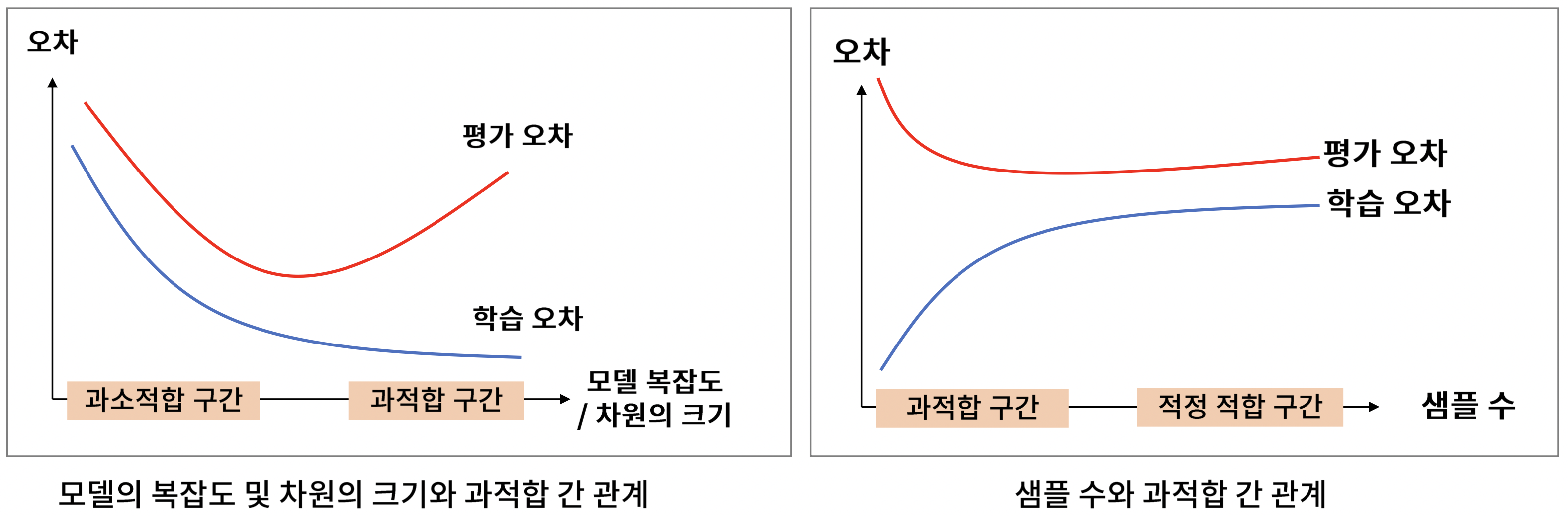
Overfitting
- 지도학습 모델은 학습 데이터를 분류/예측하는 수준
- Generalisation : 학습에 사용되지 않은 데이터도 정확히 분류/예측하는 경우
- Overfitting : 모델이 너무 복잡해서 학습 데이터만 정확히 분류/예측하는 경우
- Underfitting : 모델이 너무 단순해서 학습/검증 데이터 모두에 대해서 분류/예측 못하는 경우
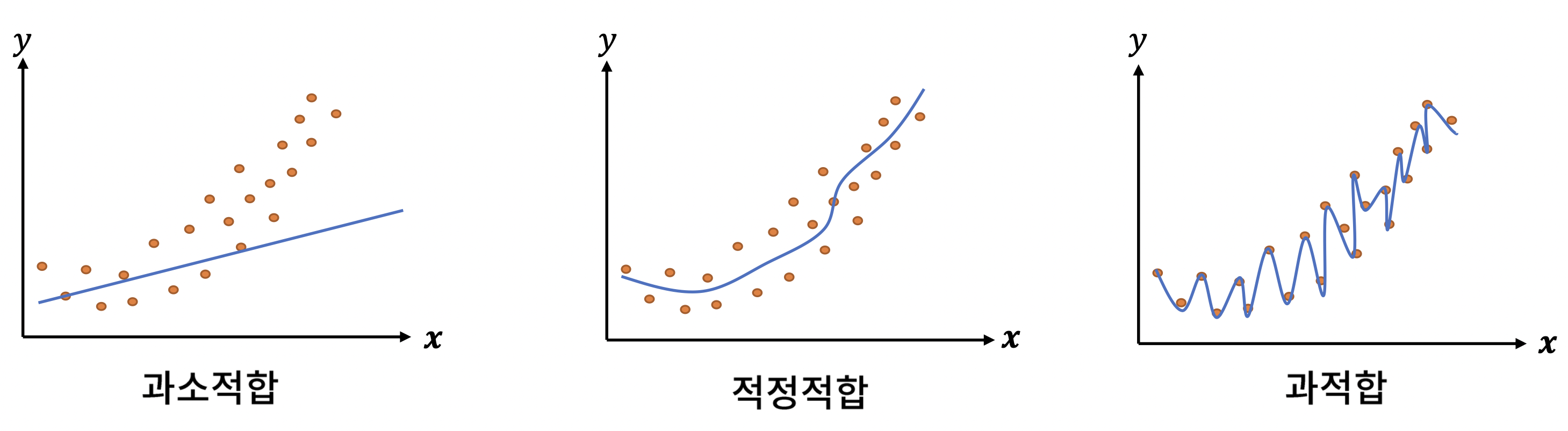
- 모델의 복잡도, 샘플 수, 차원의 크기 등이 Over/Underfitting을 야기
Data Split
- 데이터를 학습 데이터와 평가 데이터로 분할해 과적합된 모델을 정확히 평가
- 학습데이터와 평가데이터가 지나치게 유사하거나 특정 패턴을 갖지 않도록 분할해야 함
Resampling(Oversampling, Undersampling) - Cross validation, Hold-out
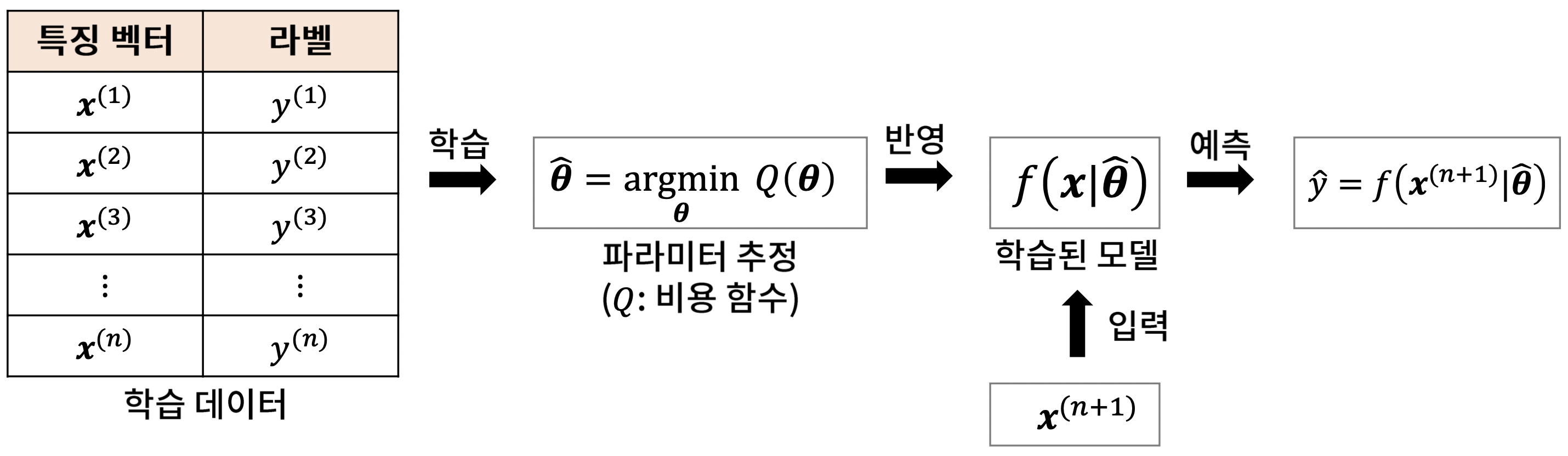
Parameter & Hyper Parameter
- Parameter
- 정의 : 모델 내부에서 결정되는 변수
- 예시 : 신경망의 가중치, SVM의 가중치
- 추정 : 비용 함수를 최소화하는 값으로 미리 정의된 컴퓨터 연산을 통해 추정
- Hyper Parameter
- 정의 : 파라미터에 영향을 주는 파라미터
- 예시 : 신경망의 은닉층 구조, SVM의 커널
- 추정 : 사용자가 직접 정의하며, 최적의 설정 방법은 없고, 휴리스틱한 방법이나 경험에 의한 설정이 대부분
Metrics for Classification Model
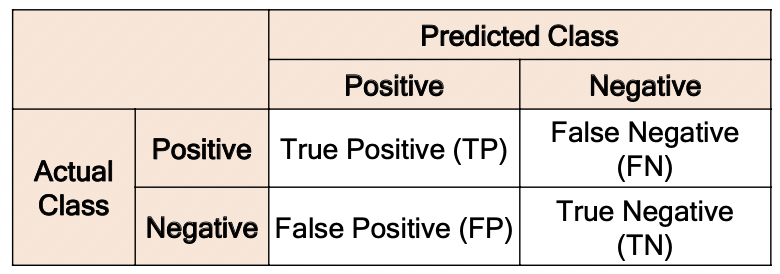
Confusion Matrix
- 분류 모델을 평가하는데 사용하는 표
Metrics
- Accuracy
- 정의 : 모든 샘플 가운데 정확히 분류한 샘플의 비율
- 주의 : 클래스 불균형 문제가 있는 데이터에 대해 매우 취약
- Precision
- 정의 : 긍정이라고 분류한 샘플 가운데, 실제 긍정인 샘플의 비율
- 주의 : 긍정이라고 분류하는 샘플 수가 작으면 작을수록 정밀도가 높아짐
- Recall
- 정의 : 실제 긍정 샘플 가운데, 긍정이라고 분류한 샘플의 비율, 검출력과 관련있음
- 주의 : 모든 샘플을 긍정이라고 분류하면 재현율이 높아짐
- F1-Score
- 정의 : 정밀도와 재현율의 조화 평균
Metrics for Multiple Classification Model
- 각 클래스를 긍정으로 간주해 평가 지표를 계산한 뒤, 이들의 산술 평균이나 가중 평균으로 평가
Metrics for Regression Model
- RMSE(Root Mean Squared Error), MSE, MAE(Mean Absolute Error), R2
ML process
1. Define the problem
- 전체 프로세스 가운데 가장 중요한 단계
- 과업 종류 결정(분류, 예측 등), 클래스 정의, 도메인 지식 기반의 특징 정의, 사용 데이터 정의
- 부적절한 문제정의
- 구체적이지 않거나, 부적절한 피처 선택, 수집 불가한 데이터
2. Collect data
- 크롤링, 센서, 로그 등으로 데이터 수집
- 기업 내 구축된 DB에서 SQL을 통해 추출하는 경우(로그)가 가장 많음, 이 경우는 클래스(로그타입) 중심으로 로드
- 부적절한 데이터 수집
- 측정오류 등으로 수집한 데이터가 실제 상황을 반영하지 못하는 경우, 해결하고자 하는 문제와 무관한 데이터를 수집한 경우, 특정 이벤트가 데이터에 누락된 경우 등
3. EDA
- 데이터가 어떻게 생겼는지 확인하여 프로세스를 구체화하는 단계
- 변수별 분포, 변수간 상관성, 이상치와 결측치, 변수 개수, 클래스 변수 분포 등을 확인하며 이 탐색 결과는 데이터 전처리 및 모델 선택에 큰 영향을 미침
1) 데이터 크기 확인 과적합 가능성 확인 및 feature 선택
2) 특징별 기술 통계 특징 변환 및 이상치 제거
3) 특징 간 상관성 VIF 10 이상 피처 확인, 차원축소, AIC벌점화 등 피처 삭제
4) 결측치 분포 결측치 제거 및 대체(KNN SMOTE)
5) 변수 개수 차원 축소, 다중공선성 확인
6) 클래스 변수 분포 비용민감 모델 및 resampling
4. Preprocess data
- 모델의 학습 및 성능을 위해 데이터를 알맞게 가공하는 단계
- 결측치 처리, 데이터 통합, 이상치 제거, 리샘플링, 특징선택, 더비변수생성 등
- 로그변환 장점
- ㅇ<x<1 범위에서 기울기가 매우 가파르고 짧다. 즉 x구간은 짧고, y구간은 음의 무한대~0으로 매우 크다.- 따라서 0에 가깝게 모인 값들이 x로 입력되면, 그 함수값인 y 값들은 매우 큰 범위로 벌어진다. 로그함수는 0에 가까운 값들이 조밀하게 모여있는 입력값을 넓은 범위로 펼칠 수 있는 특징이 있는 것.반면, x값이 점점 커짐에 따라 로그함수의 기울기는 급격히 작아지면서 y값이 큰 차이 없이 좁은 구간 내에 모이게 된다.
- 결과적으로 데이터의 분포를 모았을 때 밀집되어 있는 부분은 퍼지게 퍼져있는 부분은 모아지게 만들 수 있는 것. 즉, 한쪽으로 치우친 분포를 로그변환을 취하면 정규분포화 시킬 수 있다.
- 로그변환시 np.log() -> np.log1p() : x=0이면 음의 무한대를 갖기 때문에, x+1을 해줘서 음의 무한대를 0으로 변환시키는 것.
- 로그변환 장점
5. ML modelling
- 모델 선택
- 데이터 특성, 성능, 설명력 등을 기준으로 모델 선택
- 설명력이 중요한 경우 의사결정나무, 베이지안 네트워크 사용 - 이진 텍스트 분류시 나이브베이즈 혹은 SVM을 사용
- 데이터 특성, 성능, 설명력 등을 기준으로 모델 선택
- 하이퍼 파라미터 설정 : 모델 성능을 결정
- 모델 학습 : 모델에 포함된 파라미터 추정
6. Verify the model
- Classification
- Accuracy : 전체 샘플 가운데 제대로 예측한 샘플의 비율
- Precision : 긍정이라고 예측한 샘플 가운데 실제 긍정 샘플의 비율
- Recall : 실제 긍정 샘플 가운데 제대로 예측된 샘플의 비율- f1 : 정밀도, 재현율의 조화평균
- Regression
- MSE, RMSE, R2, MAE, MAPE, etc. - 잘못된 평가를 피하기 위해, 둘 이상의 평가 지표를 쓰는 것이 바람직
7. Report
- 구성 : 분석 목적, 데이터 탐색 및 전처리, 분석방법, 분석결과 및 활용방안
ML models
1. Regression Model
- 𝑓𝒙(𝑖) = 𝑤1𝑥(𝑖)+𝑤2𝑥(𝑖)+⋯+𝑤𝑑𝑥𝑖 +𝑏
- 𝒘 = (𝑤1,𝑤2,⋯,𝑤𝑑)𝑇
- b : bias
- 피처간 스케일 차이에 크게 영향을 받으므로, 예측 모델링할 때 스케일링이 필요
2. Logistic Regression Model
- 비용함수 : 크로스 엔트로피
- 피처 구간별 라벨의 분포가 달라지는 경우, 적절한 구간을 나타낼 수 있도록 특징 변환이 필요
3. KNN(K-Nearest Neighbors)
- 샘플 i의 k개 이웃 샘플들의 클래스 최빈값으로 분류
- 예측 : 샘플 i의 k개 이웃 샘플들의 클래스 평균으로 예측
- 주요 파라미터 설정 방법
- k : 홀수. 특징 수 대비 샘플 수가 적은 경우, k를 작게 설정해야 함
- 거리 및 유사도 척도
- 맨하탄 거리 : 모든 변수가 서열형 혹은 정수인 경우
- 코사인 유사도 : 방향성이 중요한 경우(추천시스템)
- 매칭 유사도 : 모든 변수가 이진형이면서 희소하지 않은 경우
- 자카드 유사도 : 모든 변수가 이진형이면서 희소한 경우
- 유클리디안 거리
- 맨하탄 거리 : 모든 변수가 서열형 혹은 정수인 경우
- 특징 추출이 어려우나 유사도 및 거리 계산만 가능한 경우 주로 활용(예: 시퀀스 데이터)
- 모든 특징이 연속형이고, 샘플 수가 많지 않을 때 좋은 성능
- 특징 간 스케일 차이에 크게 영향을 받아, 스케일링이 반드시 필요(*코사인 유사도 사용하는 경우 제외)
4. Decision Tree
- 예측 과정을 잘 설명할 수 있다는 장점 때문에 많은 프로젝트에서 활용
- 고객의 이탈여부를 예측하고 그 원인을 파악- 밸브의 불량이 발생하는 공정상 원인을 파악
- 방송 조건에 따라 예측한 상품 매출액 기준으로 편성표를 추천하고, 그 근거를 파악
- 선형 분류기라는 한계로 예측력은 떨어지나, 앙상블 모델의 기본 모형으로 활용됨
- 주요 파라미터
- max_depth : 최대 깊이. 크기가 클수록 모델 복잡도 증가
- min_samples_leaf : 잎 노드에 있어야하는 최소 샘플 수. 크기가 작을수록 모델 복잡도 증가
5. Naive Bayes
- 모델 구조
- 베이즈 정리를 사용하고 특징간 독립을 가정하여 사후 확률 P(y|x)를 계산
- 가능도 P(x|y)는 조건부 분포를 가정하여 추정
- 이진형 변수 : 베르누이 분포
- 범주형 변수 : 다항 분포
- 연속형 변수 : 가우시안 분포
- 이진형 변수 : 베르누이 분포
- 특징 간 독립 가정이 굉장히 비현실적, 일반적으로 높은 성능 기대하기 어려움
- 설정한 분포에 따라 성능 차이가 크기 때문에 특징 타입이 서로 같은 경우 사용하기에 바람직
- 특징이 매우 많고 그 타입이 같은 문제(이진형 텍스트 분류)에 주로 사용
6. SVM(Support Vector Machine)
- 오차를 최소화하면서 마진을 최대화하는 분류 모델
- 커널 트릭을 활용해 저차원 공간을 고차원 공간으로 매핑
- SVR, SVC
- 주요 파라미터
- kernel : 이진 변수가 많으면 linear 커널, 연속형 변수가 많으면 rbf 커널이 잘 맞음
- C : 오차 패널티에 대한 계수, 이 값이 작을수록 마진 최대화에 클수록 학습오차 최소화에 신경쓰며, 보통 10^n 범위에서 튜닝함
- r : rbf 커널의 파라미터, 클수록 데이터 모양을 잘 잡아내지만 오차가 커질 위험이 있다. C가 커지면 r도 증가시키는 방식으로 튜닝함
- 파라미터 튜닝이 까다로운 모델이지만, 튜닝만 잘하면 좋은 성능을 보장
7. Neural Network
- 초기 가중치에 크게 영향을 받는 모델, 세밀하게 random_state, max_iter 값을 조정해야 함
- 은닉노드가 하나 추가되면 그에따라 하나 이상의 가중치가 추가되어, 복잡도가 크게 증가
- 모든 변수 타입이 연속형인 경우 성능이 잘 나옴, 은닉층 구조에 따른 복잡도 조절이 파라미터 튜닝에서 고려해야할 가장 중요한 요소
- 특정 주제(시계열 예측, 이미지 분류, 객체 탐지 등)를 제외하고는 깊은 층의 신경망은 과적합 이슈가 자주 발생
8. Ensemble w/ Tree
- 의사결정나무를 기본으로 하는 앙상블 모형이 인기(좋은 성능)
- Random Forest : 배깅 방식으로 여러 트리를 학습하여 결합한 모델
- 트리의 개수, 나무의 최대 깊이를 조정해야 한다
- XGboost & LightGBM : 부스팅 방식으로 여러 트리를 순차적으로 학습하여 결합한 모델
- 트리의 개수, 나무의 최대 깊이, 학습률을 조정해야 한다.
- 트리의 개수 : 많을수록 좋은 성능을 내지만, 어느 수준 이상에서는 거의 큰 차이 없음
- 나무의 최대 깊이 : 4이하로 설정해줘야 과적합 피할 수 있음
- 학습률 : 작을수록 과소적합 야기, 클수록 과적합 야기. 통상적으로 0.1