meta-learning sparse implicit neural representations, 줄여서 meta-sparse INR 이라고 하는 이 논문은 21년 NeurIPS에 실린 논문입니다.
Background
이 논문의 핵심이 되는 개념은 meat-learning과 pruning입니다.
meta-learning (few-shot learning)
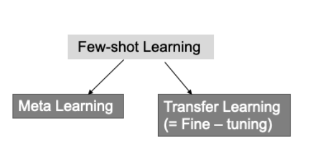
few-shot learning은, 소량의 데이터만으로도 뛰어난 학습을 하는 모델을 만들기 위해 제안된 방법 입니다. 이 방법으로 고안된 학습 방식에는 meat-learning과 transfer learning이 존재합니다.
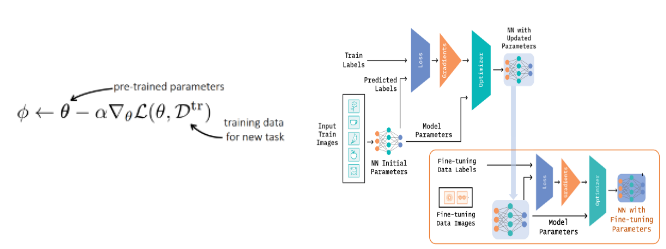
transfer learning은 대량의 데이터로 pretrained 모델을 생성한 뒤, 적은 dataset을 fine tuning하는 알고리즘에 초점을 두고 있습니다. transfer learning에서 multi task learning을 할 때는 pretrained모델을 불러온 뒤 각각의 task에 맞게 fine-tuning 합니다. 이 학습의 목표는 new task를 위한 최적의 파이를 구하는 것입니다.
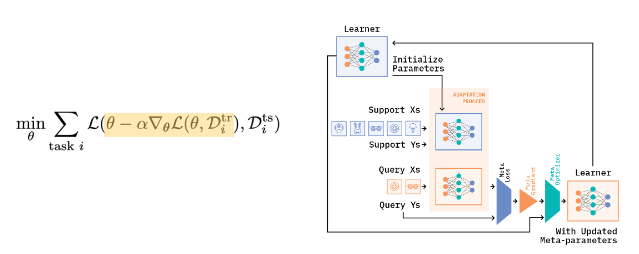
반면, 메타러닝에서는 전체학습 이후 소량의 데이터만으로도 여러 task에 대해 추론할 수 있는 범용적인 모델을 생성합니다. 이를 위해 메타 러닝 학습과정에서는 전체 데이터를 여러개의 support data, query data로 쪼개는 과정이 필요합니다. 이것을 에피소드 학습 방법이라고 합니다.
(query Xs, Ys가 validation data, support Xs, Ys가 train data)

화면에 나온, 5개의 class를 분류하는 image classifier를 만든다고 가정해보겠습니다. 기존의 경우 데이터를 train, test데이터로 분류하고 쥐, 소, 호랑이, 토끼, 용 모든 클래스 데이터를 사용하기에 학습과 시험의 도메인이 동일합니다.
에피소드 학습방법의 경우 한번에 쥐, 소, 호랑이, 토끼, 용 모든 클래스를 활용하지 않고, 여러 태스크로 쪼갠 후 테스트에서는 완전히 새로운 데이터로 분류 성능을 확인하는 방식입니다. 오른쪽 이미지처럼, train시에는 고양이, 자동차, 사과, 귤로 학습을 진행하고 테스트시에는 원숭이, 자전거라는 아예 새로운 데이터로 성능을 확인하는 방식입니다.
이처럼 학습에 활용되지 않은 클래스의 데이터에 대해서도 어느 정도의 성능을 보장하도록 하는것이 메타러닝의 목표입니다.
Introduction
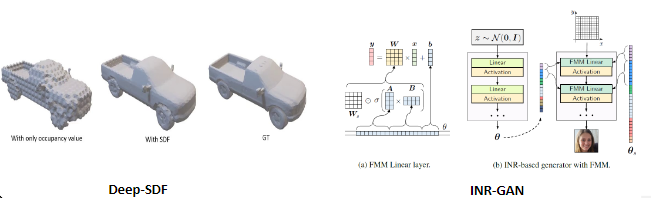
INR은 pixel이나 voxel과 같은 좌표 격자에 상응하는 값을 저장하는 대신, relu나 sinusoid같은 continuous activation function들을 사용한 신경망을 저장함으로써 새로운 방식의 signal representation을 제시했습니다.
activate func.의 continuous함은 SR이나 inpainting tasks에서 out of the box 메소드를 제공하고, 신호의 차원 또는 해상도에 따라 엄격하게 스케일링되지 않는 매개변수 수를 갖거나 (이것은 신호의 차원이나 해상도가 달라져도 매개변수를 크게 바꿀 필요 없다는 뜻으로 보입니다), signal들로부터 prior를 학습하여 img generation이나 view synthesis에도 이용할 수 있는 특징이 있습니다.
이러한 장점을 보여주는 기존 연구로는 DeepSDF, INR-GAN 등이 존재합니다.
Related Works
하지만 이러한 장점들에도 불구하고 신호의 크기가 커진다면, INR은 여전히 많은 양의 메모리와 계산량을 필요로 하는 단점이 존재합니다. 기존에 이 메모리와 계산량을 줄이기 위해 여러 방면으로 접근했었고, 세 가지 카테고리로 나눌 수 있습니다.
-
Category 1. (0, 0), (1,2) 따위의 입력 좌표계를 1d vector상에 나타낸 latent code vector를 입력으로 취하고 그에 따라 INR 출력을 수정하는, neural network sharing across the signal 구조를 사용한 접근입니다. 이 방식은 새로운 signal에 대해서는 표현력이 저하되는 단점이 있습니다.
-
Category 2. 앞서 설명드렸던 meta-learning approach를 채택한 경우입니다. 이 경우에는 메모리 요구량이 줄어들지 않았다고 적혀있으며, 계산량에 대한 언급은 없었습니다.
-
Category 3. 모델의 가중치를 float type에서 int type으로 uniformly quantizing 하는 방법을 시도했습니다. 이 방법에서는 모델 파라미터를 저장하는데 필요한 메모리의 크기는 줄일 수 있었으나, 각각의 signal을 학습시키는데 필요한 optimization step의 수, 즉 계산량을 줄이지는 못한다는 단점이 존재했습니다.
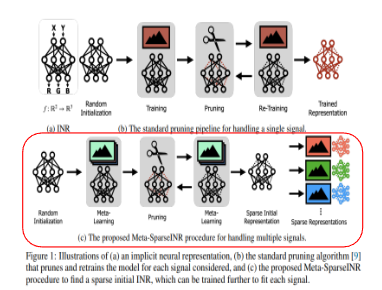
위 3가지 카테고리 각각의 단점들을 해결하기 위해, 논문에서는 자주 사용되지 않는 파라미터를 0으로 보내는 network pruning 기반의 framework를 제시합니다. 이 framework를 통해 다양한 signal set들을 표현할 수 있는 sparse한 INR을 학습하는 것이 framework를 제시한 목표이기도 합니다. 목표를 달성하기 위해, 앞서 제시한 문제를 다음과 같이 표현합니다.
‘적은 수의 optimization step만 가지고, 각각의 signal을 잘 표현할 수 있도록 학습이 될 수 있는 sparse initial INR를 찾자.’
이 표현대로라면 각각의 INR에 대해 prune-retrain하는 cycle을 반복할 필요가 없어집니다. 이러한 pruning algorithm을 Meta-SparseINR이라고 명명했으며, 이것이 INR setup에 대해서는 첫 번째로 pruning을 적용한 알고리즘이라고 말했습니다.
A framework for efficiently learning sparse neural representations
논문의 목표를 다시 정리해보면, large number signal에 대해 INR을 학습, 저장할때 메모리와 계산상의 효율을 얻을 수 있는 framework를 개발하는 것입니다. 이것을 formulate하면 well-initialized sparse subnetwork structure를 찾아내는 문제로 볼 수 있습니다.
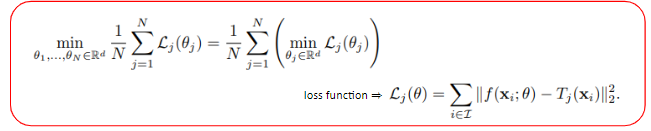
Tj는 우리가 근사해야할 target signal이고, f(x,θ)는 coordinate vector를 signal value로 mapping해주는 함수일때, j번째 target signal의 손실 함수 Lj(θ) 는 이와 같이 정의할 수 있습니다. N개의 target signal에 대해 loss를 최소화하는 방법은 각 signal의 손실을 최소화 하는 INR의 파라미터, 즉 θ를 찾아내는 문제로 볼 수 있습니다. 여기까지는 통상적으로 INR이 학습하는 과정과 동일합니다.
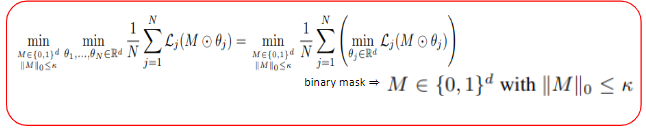
여기에 pruning을 적용해보겠습니다. 논문에서는 pruning을 적용할 때, 사용하지 않는 weight parameter들을 0으로 보내는 방법을 사용하였는데, 이것은 binary mask M을 model parameter에 element-wise곱을 하는 방식으로 나타낼 수 있고, 결국 위 식을 만족하는 binary mask M을 찾는 문제로 볼 수 있게 됩니다.

그리고 논문에서는 이 식에서 너무 많은 gradient 계산을 하지 않기 위해서 ‘good initialization’의 필요성을 언급하고있습니다. 이전 식까지는 target signal이 N개 존재하면 각각의 signal에 fitting을 진행한 INR 모델도 마찬가지로 N개가 존재했으나, 이 식에서는 초기에 ‘good initialization’을 통해 초기화시킨 weight를 각각의 signal에 대해 fit시키고 그에 대해 loss를 구하는 방식으로 바뀌었습니다.
즉 N개의 random initialization된 모델의 파라미터를 업데이트하는 것에서, 1개의 good initialization된 모델을 fine tuning시키는 것으로 문제를 바꾼 것입니다.
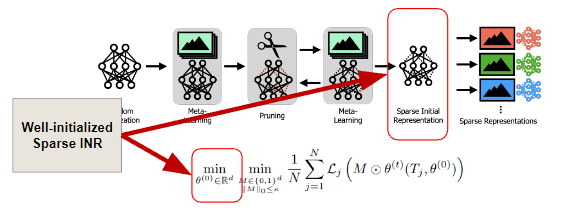
여기서, 각각의 signal이 효과적으로 train될 수 있는 well-initialize sparse INR를 찾기 위해서는 meta-learning approach가 필요합니다. 논문에서는 INR에 meta-learning을 적용하여 INR이 빠르게 각각의 signal에 적응할 수 있도록 하고, pruning을 할 때도 random하게 pruning하는 것이 아니라, weight의 magnitude에 기반하여 model을 pruning합니다.
Learning sparse neural representations with meta-learning
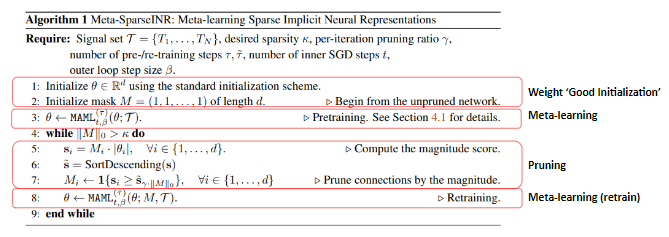
이것은 Meta-SparseINR의 학습 과정을 나타낸 알고리즘입니다. 요약해보면 Meta-SparseINR는 MAML이라는 메타 러닝 알고리즘을 이용하여 INR를 학습하고 magnitude-based pruning을 이용하여 INR를 pruning하는 과정을 반복하며 작동한다고 할 수 있습니다.
첫번째 단계는 weight initialization과 meta learning을 묶어서 한 단계로 취급합니다. signal set이 주어졌을때, SIREN에서와 동일한 스키마로 random하게 초기화된 INR에 대해 일정 step만큼 MAML을 반복합니다.
두번째 단계는 pruning으로, 학습된 INR에서 weight magnitude가 작은 순서대로 일정%만큼 연결을 제거합니다.
세번째 단계는 retraining으로, pruning된 INR를 다시 MAML을 이용하여 정해진 step만큼 학습합니다. retrain이 끝났는데도 아직 모델 파라미터가 특정 값보다 크다면 다시 반복하여 진행합니다.
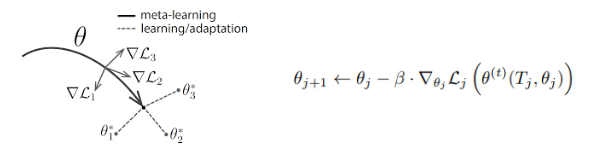
논문에서는 meta-learning을 할 때 MAML이라는 알고리즘을 사용합니다. N개의 signal set T가 있을때, signal set으로부터 한 개 이상의 signal을 뽑습니다. signal을 뽑고 나서, learner는 t step만큼 SGD등을 이용하여 현재 파라미터 θj를 업데이트 합니다. 즉 초기 parameter가 있을 때, Tj라는 이미지에 대해 t번만큼 학습 epoch를 돌린 것으로 생각할 수 있습니다.
이 학습된 θt에 의해, θj는 θ(j+1)로 업데이트가 됩니다. 이렇게 θj가 θ(j+1)로 업데이트 되는 것이 MAML을 한번 수행한 것이며, 앞선 알고리즘에서는 이것을 여러번 반복합니다.
이미지의 오른쪽 식에서는 signal을 Tj하나만 뽑는다고 가정했지만, 왼쪽과 같이 signal을 여러 개 뽑을 때는 각각의 gradient가 가리키는 방향을 모두 고려하여 새로운 세타를 업데이트합니다.
pruning은 위쪽 Algorithm 1의 5, 6, 7 line과 같이, 파라미터를 내림차순으로 정렬하고, 크기가 작은 파라미터들은 값을 0으로 보내는 방식으로 진행합니다.
이렇게 meta learning, pruning을 반복하며 모델의 크기를 줄인 것이 meta-sparseINR입니다.
Experiments

실험에 사용한 데이터셋은 face dataset인 CelebA, 자연 이미지 데이터셋인 Imagenette, 기하학적 패턴의 데이터셋 2D SDF 3개의 데이터셋을 사용했으며, 178x178로 resize 및 crop을 적용했습니다. 실험에 사용한 모델은 SIREN과 동일하게, sinusoidal activation function을 갖는 MLP를 이용했습니다.

학습에 사용된 메소드는 이와 같이 총 6개가 있는데, Meta-sparseINR가 ours입니다. 여기서는 pruning 비율을 20%로 잡았습니다.
random pruning은 magnitude-based pruning이 아니라 random pruning을 적용한 모델입니다.
Dense-Narrow는 original INR보다 더 dense하지만, 더 narrow한 width를 갖는 neural representation을 meta-learning 시킨 것입니다.
MAML+oneshot과 MAML+IMP는 pruning을 meta learning 하고나서 하는 것이 아니라, fine tuning을 진행할 때 한번 또는 여러번 하는것입니다.
scratch는 Dense-narrow와 같지만, 메타러닝을 하지 않은 것입니다.

이 그림처럼, dense-narrow는 pruning을 진행할 수록 색에 대한 정보나 structure정보등을 잃어버리는데 반해, meta-sparseINR는 그 정보를 어느 정도 보존하는 것을 볼 수 있습니다.
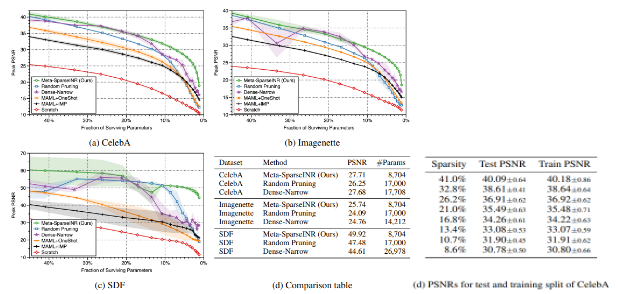
3가지 종류의 데이터 셋에 대해, pruning을 많이 하더라도 다른것들에 비해 모델의 표현력이 우수한 것을 볼 수 있습니다. 또한 d의 파라미터 숫자를 보더라도 다른 것들보다 적게는 절반, 많게는 33%정도의 파라미터만 가지고 있음에도 표현력은 오히려 높음을 볼 수 있습니다.
여기서 한가지 주목할 것은 random pruning이랑 dense-narrow가 MAML+oneshot과 MAML+IMP보다 성능이 좋다는 것입니다. 이는 compressed된 model로부터 traning을 시작하는 것이, 나중에 각각의 signal에 fitting할때 model을 compress하는것보다 beneficial함을 나타낸다고 합니다.
가장 오른쪽의 d. PSNRs for test and training split of CelebA는 meta-sparse SIREN에 대해 training과 test의 PSNR을 비교한 것으로서, compressed initial INR을 training하는것이 test데이터의 unseen sample에 대해서도 generalization을 잘 하는 것을 알 수 있습니다.
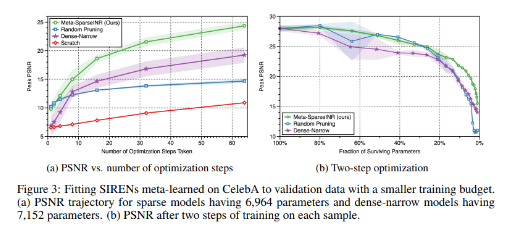
다음 표는 optimization step의 수와 pruning의 정도에 따라 모델의 성능을 비교하는 그래프 입니다. 왼쪽의 (a)는 하나의 signal당 몇번의 optimization step을 거치느냐에 따라 PSNR을 비교한 것인데, meta-sparseINR이 최상위에 위치한 것을 볼 수 있습니다. 논문에서는 또 하나 흥미로운 점을 제시했는데, Dense-narrow가 random pruning보다는 초기에 낮은 성능을 보이나 optimization step을 증가시키면 더 좋은 성능을 보여준다는 점입니다.
이것을 논문에서는 dense모델의 단점은 그들의 표현력에서 오는것이지, 학습을 얼마나 효율적으로 하는지는 관계가 없다고 추정했습니다. (결국 step수를 늘리면 dense모델과 random pruning의 성능이 비슷해지기 때문인 것으로 생각됩니다.)
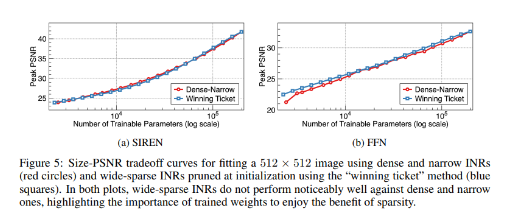
이 그래프는 meta-learning이 정말 효과가 있었는지를 보여주는 그래프들입니다. 아무것도 pruning을 하지 않은 dense-narrow와, 기존 pruning 방법들 중 가장 효과가 좋다고 알려진 winning ticket방식 두 가지에 대해 SIREN, FFN 두 모델 구조로 실험을 진행했습니다. meta learning없이 일반적인 INR 학습 방식으로 진행했을 때, 두 방식 모두 큰 차이가 없는 것을 알 수 있습니다.
즉, 단순히 pruning하는 것만으로는 큰 효과를 볼 수 없고, 메타 러닝을 적용해야만 효과가 나온다는 것을 알 수 있습니다.
Discussion & Limitations
결론적으로, 이 논문은 메모리와 계산량의 관점에서, INR를 효율적으로 학습할 수 있는 framework를 제안한 것으로 볼 수 있습니다. 그리고 이 framework를 찾기 위해 적은 수의 training으로도 각각의 signal에 잘 fitting되는 sparse INR를 찾는 Meta-SparseINR라는 알고리즘을 첫번째로 제안했습니다.
pruning approach를 채택할때는 논문에서는 두가지 가정을 하였습니다. 첫번째로 앞서 M이라고 하는 binary mask를 추가한 sparse parameter와, 두번째로 shared parameter가 존재하지 않는다는 것이었습니다. 하지만 efficiency를 위해서는 반드시 이런 가정이 필요한 것은 아니고, 다른 접근법도 존재할 수 있으며 이는 이후의 연구 과제로 남겨놓았습니다.
limitaion으로는 이와같은 네트워크 압축 알고리즘이 다양한 윤리적 문제를 야기할 수 있다는 점과, 일정 성능까지 끌어올리는데 소요되는 훈련 시간의 상이함, 표현되는 이미지의 구조적으로 편향된 왜곡이 발생할 수 있다는 점을 들어 사용하기 전에 충분히 고려를 해야 한다고 언급하였습니다.
