A Novel Image Quality Assessment With Globally and Locally Consilient Visual Quality Perception Review
Paper review
Introduction
많은 img processing과 CV application은 visual quality를 maximizing하고 인식되는 distortions을 minimizing하는데 목표를 두고 있기 때문에, 좀 더 정교한 image quality assessment (IQA)을 개발하는것이 매우 중요해졌습니다. IQA메소드는 full-reference(FR), reduced-ref(RR), no-ref(NR)로 나뉘는데, 이 논문에서는 1번식과 같이 visual quality score를 계산하는 FR-IQA 메소드에 중점을 두었습니다.
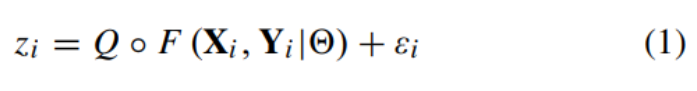
식에서 X는 원래 이미지, Y는 왜곡이 발생한 이미지, Θ는 모델 파라미터, F가 FR-IQA 메소드, ε은 prediction error이고 Q는 FR-IQA의 예측값과 quality score사이에 nonlinear한 관계가 있기 때문에 넣어준 non linear function입니다.
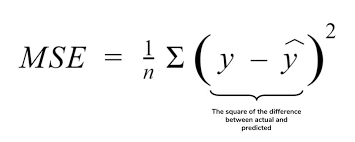
기존의 metric들중 대표적으로 mean squared error는 계산하기 쉽고 수학적으로 바람직한 속성을 가지고 있지만, 왜곡에 대해서는 우리 눈이 감지하는 것 만큼 잘 나타내지 못한다는 단점이 있습니다. 그래서 대다수의 FR-IQA 메소드들은 사람이 주관적으로 느끼는 정도인 subjective visual quality score들과 일치하도록 개발되고 있습니다.
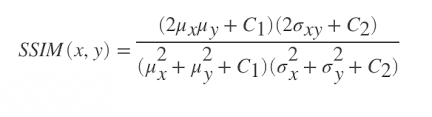
한편 SSIM은 human visual system (HVS)이 시각인식을 할 때 image texture로부터 구조적인 정보를 뽑아낸다는 가정에 기반을 두고 있습니다. HVS가 시각적으로 인식을 할 때는 image signal의 대비/구조적 이미지를 주요 feature로 사용한다는 특징또한 SSIM이 제시하였습니다.
논문에서는 3가지 contribution을 제시합니다.
- Based upon our best knowledge, we firstly reveal that HVS has different strategies in perceiving visual quality depending jointly on different image texture characteristics and distortion types.
첫번째는 HVS가 왜곡의 종류나 이미지 texture에 따라 visuql quality를 인식하는 전략을 다르게 취한다는 사실을 드러낸 것입니다. 이것에 기반하여, 다양한 image texture와 왜곡 type에도 일관되게 인식이 될 수 있는 adaptive한 feature를 채택하는것이 FR-IQA의 성능을 향상시킬수 있다는 결론을 도출할 수 있습니다.
- We propose a novel FR-IQA method, called Structural Contrast-Quality Index (SC-QI) by adopting a Structural Contrast Index (SCI)
두번째 contribution은 SCI를 채택한 SC-QI라는 새로운 FR-IQA method를 제안한 점입니다. SC-QI에는 색채 구성의 변화와 대비 감도와 같은 property를 효과적으로 반영한 feature들도 추가되어 있다고 나와있습니다. 그 결과 다른 SOTA FR-IQA method에서는 하지 못했던, 수많은 왜곡된 이미지들의 특성에 대한 글로벌 및 로컬 시각적 품질을 정량화할 수 있는 장점이 있습니다.
- We also introduce a modified version of SC-QI, called Structural Contrast-Distortion Metric (SC-DM)
마지막으로 SC-QI의 modified version, normalize distance metric에 기반한 SC-DM을 제시하였습니다.
Related Works
A. Two important Characteristics of HVS
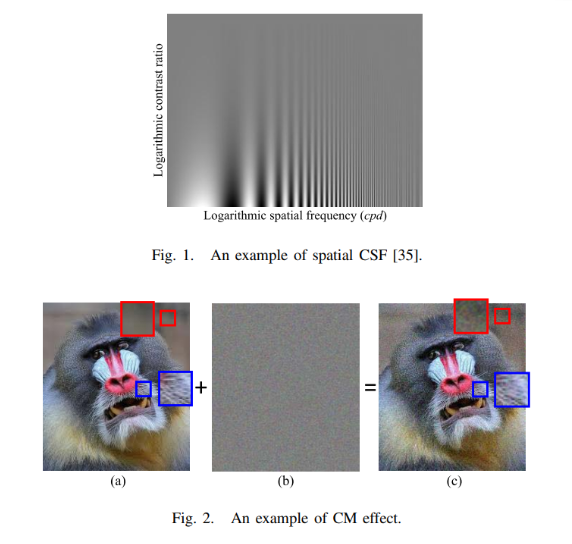
HVS에는 두 가지 중요한 특성이 있습니다. 하나가 CSF, 다른 하나가 CM입니다. spartial CSF는 HVS가 공간적 주파수에 따라 왜곡을 감지하는 정도가 달라진다는 것을 나타냅니다.
fig 1은 HVS는 공간 주파수에 따라 정현파 격자 패턴의 변화에 대한 시각적 인식 감도가 달라 밴드 패스 특성을 보여준다고 합니다.
CM effect는 HVS가 배경 이미지의 텍스처 특성에 따라 왜곡을 감지하는 정도가 달라진다는 것을 나타냅니다. fig2는 그 예시를 보여줍니다. 이미지에서 texture가 homogeneous한 부분과 complex한 부분 각각에 대해 원 이미지에 노이즈를 주었을 때, 우리눈은 빨간 박스에서는 왜곡을 쉽게 감지할 수 있지만, 파란 박스에서는 동일한 노이즈를 주었음에도 왜곡을 감지하기 어려운 것을 알 수 있습니다. 이것은 HVS가 image texture에 의존하여 왜곡을 감지한다는 것을 나타냅니다. 여기서 texture complexity는 대비 정도뿐만아니라 배경 텍스쳐 패턴의 구조와도 연관되어있습니다. 이때 배경의 구조성이란 이미지 패턴의 무작위성과 반비례한다고 합니다.
이런 관찰로부터 구조성과 대비 정도를 모두 고려하는 새로운 texture complexity index metric인 structural contrast index, 줄여서 SCI가 제안되었습니다. 이 논문에서는 SCI를 FR-IQA method의 key feature로 사용할 예정입니다.
B. SCI
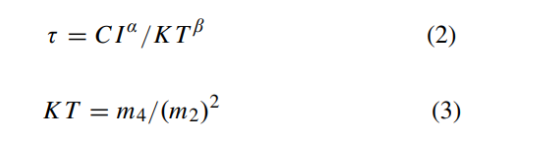
그렇다면 이제 SCI에 대해 알아보겠습니다.
2번식이 SCI에 관한 식입니다. SCI를 나타내는 τ는 structureness에 해당하는 KT와 contrast intensity에 해당하는 CI의 비율로 나타내어집니다. 이때 NXN크기의 DCT블록 B안에서 KT와 CI를 계산하여 SCI를 나타냅니다. 여기서 α, β는 모델 파라미터입니다.
KT는 텍스쳐 패턴의 랜덤성을 나타내고, DCT AC 계수의 크기의 첨도로 3번식과 같이 나타납니다. 2번식의 CI는 m0/N^2로 나타내지며, N은 NxN DCT블록의 높이입니다.
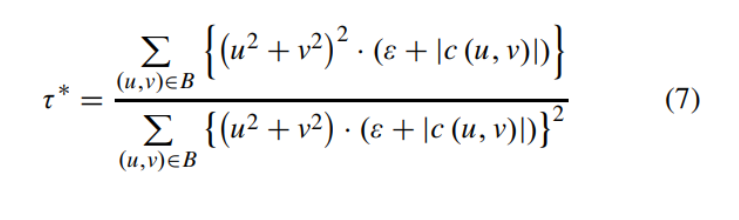
이 논문에서는 왜곡에 민감한 이미지 텍스쳐 지역일수록 더 높은 값을 갖게 하기 위해 inverse SCI를 사용합니다. 그리고 inverse SCI의 모델파라미터 ε, γ, α, β에 적당한 값을 넣어주면 inverse SCI를 7번식과 같이 간소화 할 수 있습니다. 여기서 C(u, v)는 (u, v)번째 DCT coefficient값입니다.
이렇게 계산된 SCI에 대해, 인식되는 visual quality에 대한 characterization power는 바로 다음 섹션 에서 진행됩니다.
C. Overview
섹션 C는 기존에 제시되었던 FR-IQA Method들을 overview하는 부분이지만, 하나하나 다루기에는 내용이 너무 길어질 것 같아 생략하였습니다. 기존에 제시된 FR-IQA method들의 공통점은, image signal의 대조 또는 구조적 정보가 visual quality인식에 있어 중요한 역할을 수행한다고 추정하는 것이었습니다. 그러므로 저자는 그러한 대조/구조적 정보를 효과적으로 characterize하는 feature를 찾아내는것이 효과적인 FR-IQA method를 찾는것의 주요 이슈가 될것이라고 말하고있습니다.
Proposed Structural Contrast-Quality Index Based on Structural Contrast Index
A. Our New Observation for Visual Quality Perception

이 섹션에서는 HVS는 다양한 이미지 텍스처 특성 및 왜곡 유형에 대해 시각적 품질을 '공동'으로 인식하는 전략이 다르다는 것을 보여주는 내용부터 시작합니다. Fig 3에는 세 이미지가 나와있는데, 왼쪽부터 original image, 가운데는 Additive white Gaussian noise(AGN)에 의해 왜곡된 이미지, 우측은 Gaussian Blur(GB)에 의해 왜곡된 이미지입니다. 각 이미지에 쳐진 초록, 빨강, 노란 박스는 순서대로 균일한 texture, edge, complex texture부분을 나타냅니다. Fig 3의 AGN, GB 두 왜곡은 HVS에 다르게 영향을 미칩니다.
HVS는 AGN에 의한 왜곡을 초록 상자, 즉 homogeneous image region에서 주로 인식하고, 노란 상자, 즉 complex texture region에서는 그러한 왜곡을 잘 인식하지 못하는 경향이 있습니다.
GB에 의한 왜곡은 반대로 complex texture, edge region에서 잘 인식되고 homogeneous region에서는 HVS가 인식을 잘 못하는 것을 볼 수 있습니다.
Fig 3이 의미하는 바는, HVS는 distortion을 인식할 때 distortion type과 image texture characteristic 둘 다에 의존한다는 것입니다.
B. Analysis on Contrast/Structure Features in FR-IQA Methods

여기서는 AGN, GB 두 가지 왜곡과 관련하여 FR-IQA 메소드 상의 구조/대비 정보의 특성을 알아보기 위해 네 가지 visual feature와 비교를 합니다.
- Variance: 로컬 이미지의 대비 강도를 정량화 하기 위해 사용합니다.
- Pearson Linear correlation coefficient (PLCC): 두 local 영역 사이의 구조적 유사성을 정량화하기위해 사용됩니다.
- Gradient operator: 1차 미분 연산자를 통해 얻을 수 있습니다. 이 논문에서는 Scharr 1차 연산자를 사용했습니다.
- 4개의 directional highpass filter (4-D HF): image texture의 복잡성을 나타내는 값으로 쓰입니다.
Fig4의 variance, PLCC에 해당하는 a, b, f, g를 보면 homogeneous, edge, complex texture region에서 distortion type에 상관없이 비슷한 distortion이 발생하는것을 볼 수 있습니다. 즉 variance와 PLCC는 image texture의 characteristic을 드러내지 못한다고 할 수 있습니다.
Scharr operator의 경우, Y1과 Y2이미지의 distortion이 한쪽이 밝으면 다른 한쪽은 어두운, 음의 상관관계에 있는것을 볼 수 있습니다. 반면 4D HF feature에서는 Y1과 Y2가 양의 상관관계에 있다고 합니다.
SCI를 보면 Y1이미지는 homogeneous region에서 large distortion value를 갖는것을 볼 수 있습니다. 아까전 Fig3에서, HVS는 AGN distortion은 homogeneous region에서 발생할 때 잘 인식한다고 했었는데, 그것을 뒷받침하는 이미지라고 할 수 있습니다. 반대로 Y2에서는 edge와 complex texture region에서 large distortion value를 갖는데, 이것 또한 Fig3에서 HVS는 GB distortion을 edge와 complex texture region에서 잘 인식한다는 설명과 일치합니다.
즉, Fig 4는 SCI가 HVS의 visual quality perception, 즉 구조적 왜곡의 종류에 따라 다른 image characteristic을 사용한다는 것을 가장 효과적으로 설명하는 feature라는것입니다. 이런 점이 SC-QI와 SC-DM의 primary feature로 SCI를 사용하는 이유라고 밝혔습니다. 다만 SCI는 luminance component들의 structural distortion만을 고려하도록 고안되었기 때문에, Mean shift distortion같은 chromatic distortion에는 효과를 잘 보이지 못한다고 합니다.
C. Proposed Structural Contrast-Quality Index
A파트에서 HVS의 인식 전략을 알아보았고, B파트에서 SCI가 HVS의 인식전략을 잘 표현하는 feature인 것을 알아보았습니다. 마지막 C파트에서는 SC-QI의 계산 방법을 제시합니다.
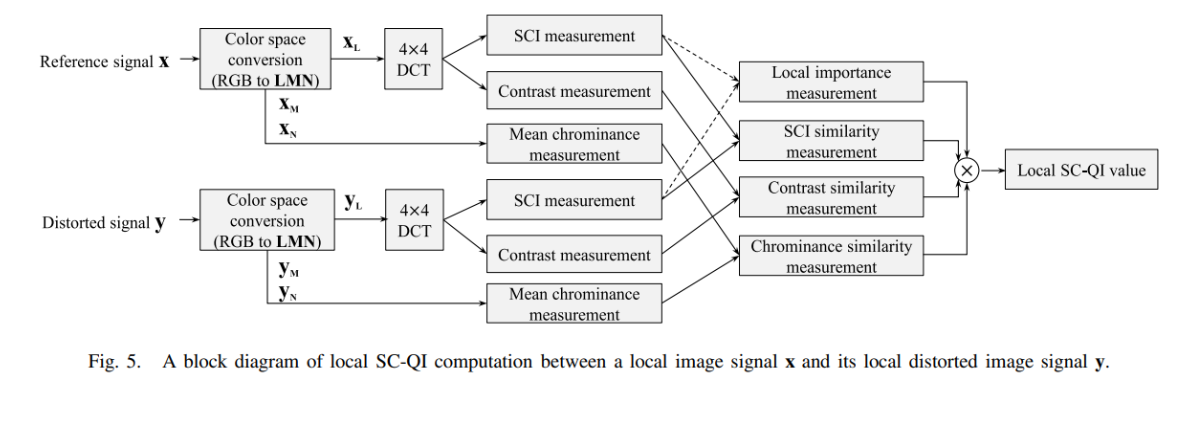
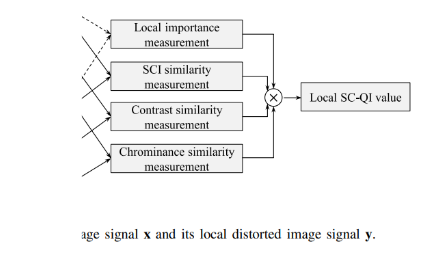
Fig 5가 SC-QI 계산과정을 블록 다이어그램으로 나타낸 것입니다. 이미지 전체에서 한번에 계산하는 것이 아니라, 4x4 image block씩 떼어와서 따로 계산하는 방식입니다. x가 원래 이미지, y가 왜곡된 이미지입니다. 이 다이어그램을 나눠서 보겠습니다.
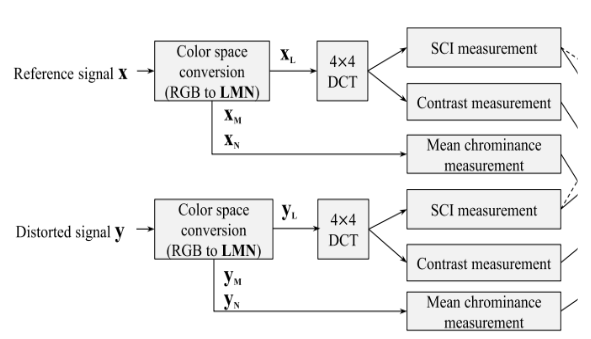
위 이미지에 나와있는 부분에 해당하는 내용을 보겠습니다.
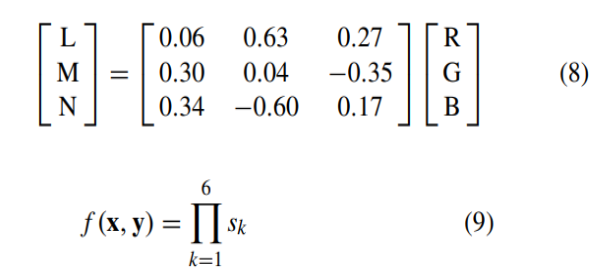
먼저 x, y signal의 pixel intensity value를 [0,1]범위 내로 normalize합니다. 이후 만약 RGB이미지라면, 휘도인 luminance, 색차인 chrominance에 해당하는 LMN color space로 8번식과 같은 계산을 거쳐 전환됩니다. XL, XM, XN은 휘도, 색차에 해당하는 local image block을 나타냅니다. 이중에서 XL만 DCT 계수로 변형되어 SCI와 frequency-dependent contrast의 feature value를 계산합니다.
이것들을 9번식과 같이 6개의 similarity measure들끼리 곱해주면 local SC-QI value값을 도출해낼 수 있습니다.
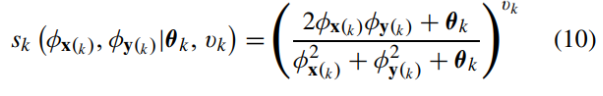
이때 각각의 similarity measure들은 10번과 같은 식을 따르며, Φx(k)는 feature function, θk는 분모가 0으로 가지 않도록 하는것이고, θk와 vk는 모델 파라미터를 나타냅니다.
예를 들어 first similarity measure s1은 Φx1이 related works에서 보았던, SCI에 inverse를 취한 수식(7)에 xL을 대입하여 얻은 값을 사용합니다.
그 다음 부분에 관한 내용입니다.
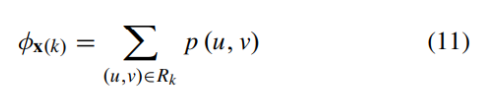
2,3,4번째 similarity measure s2, s3, s4는 HVS의 왜곡에 대한 sensitivity는 spatial frequency에 의존한다는 HVS의 contrast sensitivity function을 반영하기 위해 사용됩니다. 각각 DCT block의 low, middle, high frequency region에서 contrast energy를 비교하는 방식으로 계산됩니다. s2, s3, s4의 feature function은 식 11과 같습니다.
- To reflect this effect into SC-QI, we devise last two similarity measures s5 and s6 by comparing two average chrominance values, φx(5) = E[xM] and φx(6) = E[xN], where E[·] is the expectation operator.
similarity measure s1, s2, s3, s4는 luminance components에 관한 것이었으니, 나머지 s5, s6은 chrominance components에 관한 것입니다. s5, s6의 feature function은 expectation이며 두개의 average chrominance value를 비교함으로써 얻어낸다고 합니다.
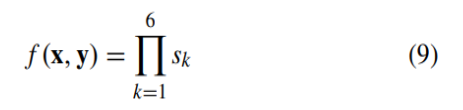
이렇게 구한 s1부터 s6의 measure들을 갖고 9번의 식을 거치면 비로소 하나의 4x4 image block의 loacl SC-QI value가 얻어집니다.
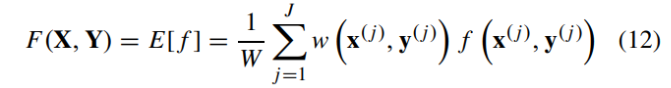
하나의 이미지에는 무수히 많은 local SC-QI value가 있으므로, 이것들을 하나로 통합하여 global perceptual visual quality value를 산출해야 합니다. 논문에서는 가중 평균을 이용한 pooling stage를 거쳐 global value를 구한다고 합니다. 식은 12와 같습니다. w(x, y)는 local weight로 논문에서는 inverse SCI를 사용했습니다.
Experimental Result
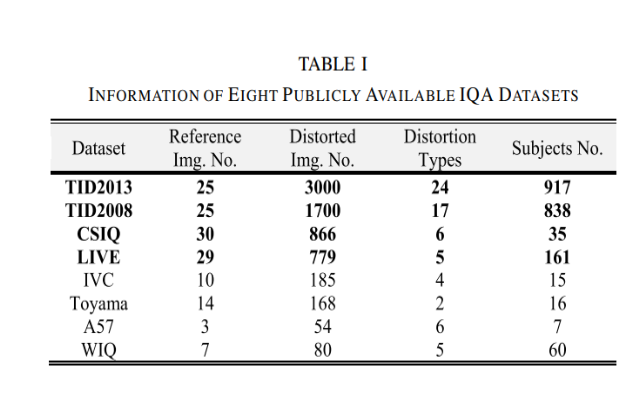
able I은 8개의 IQA dataset의 정보를 나타내고 있습니다. 논문에서는 SC-QI와 SC-DM의 성능을 기존 sota FR-IQA method들과 비교하기 위해 볼드처리된 4개의 데이터셋에 대해서 실험을 진행했습니다.

table2는 각각의 데이터셋에 존재하는 왜곡의 종류들입니다.
실험에서는 총 12개의 Fr-IQA method와 SC-QI, SC-DM의 성능을 예측 정확성과 계산 복잡도의 측면에서 비교합니다.
prediction accuracy를 비교하기 위해, 4개의 performance measure를 비교합니다.
- SROC는 단조성(monotonicity)을 평가하기 위해 사용됩니다. 단조성이 좋다는 것은 한 변수의 값의 크기가 커지면 다른 변수의 크기도 커진다는 뜻입니다.
- KROC 역시 단조성을 평가하기 위해 사용됩니다. PLCC는 선형성(linearity)이 얼마나 강한지를 측정하기 위해 사용됩니다. 선형성이 강하다는 것은 변수들의 관계가 직선에 의해 잘 모델링된다는 뜻입니다.
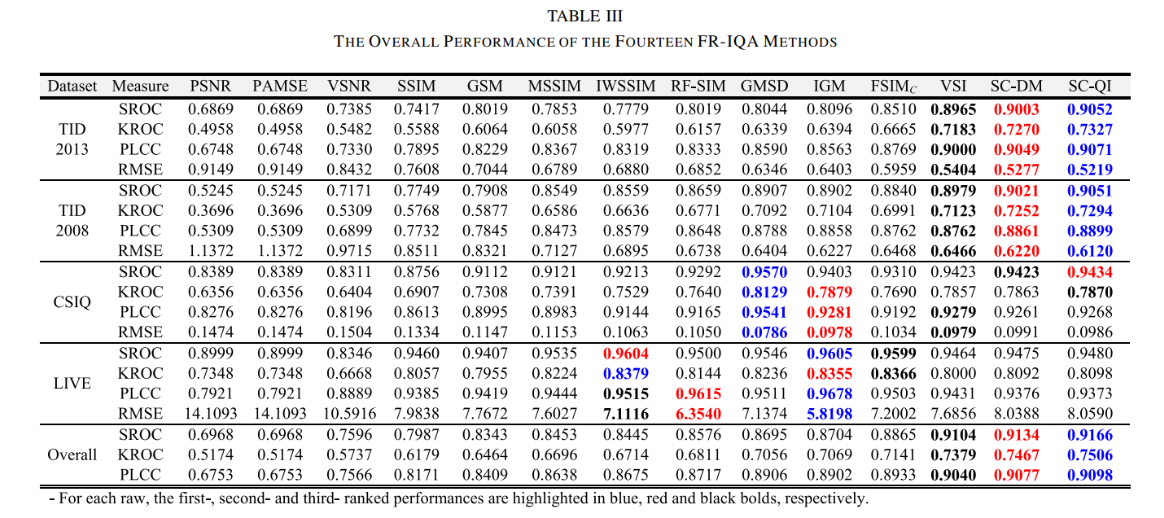
테이블 3은 FR-IQA method의 전반적인 성능을 prediction accuracy관점에서 나타낸 표입니다. 가장 뛰어난 성능을 보인 method가 파란색, 그다음이 빨간색, 세번째가 검은색으로 강조되어 있습니다.
전반적으로, 논문에서 제시한 SC-QI와 SC-QM의 성능이 SROC, KROC, PLCC 모든 부문에서 뛰어난 성능을 보이고 있습니다. 이것은 SCI가 HVS의 visual quality perception 행동전략을 잘 반영한다고 말할 수 있습니다.
그리고 SC-QI가 SC-DM을 약간 상회하는 성능을 보이고 있는데, 이것은 local quality를 계산할 때, SC-DM은 sqared distortion measure를 합하는 방식으로 계산하지만, SC-QI는 similarity measure를 곱하는 방식으로 계산하기 때문이라고 합니다.
probabilistic summation theory라고 불리는 정신 물리학 이론에서는 HVS는 서브밴드 도메인에서 적어도 하나의 신호 성분이 다양한 신호 성분들 사이에서 눈에 띄게 왜곡될 때, HVS가 왜곡을 인식한다고 주장하며, 그렇기에 곱셈연산이 있는 SC-QI가 SC-DM보다 HVS의 본질적 행동에 더 일치한다고 설명하고있습니다.
