[ Algorithm ] 03. Divide and Conquer

Recurrences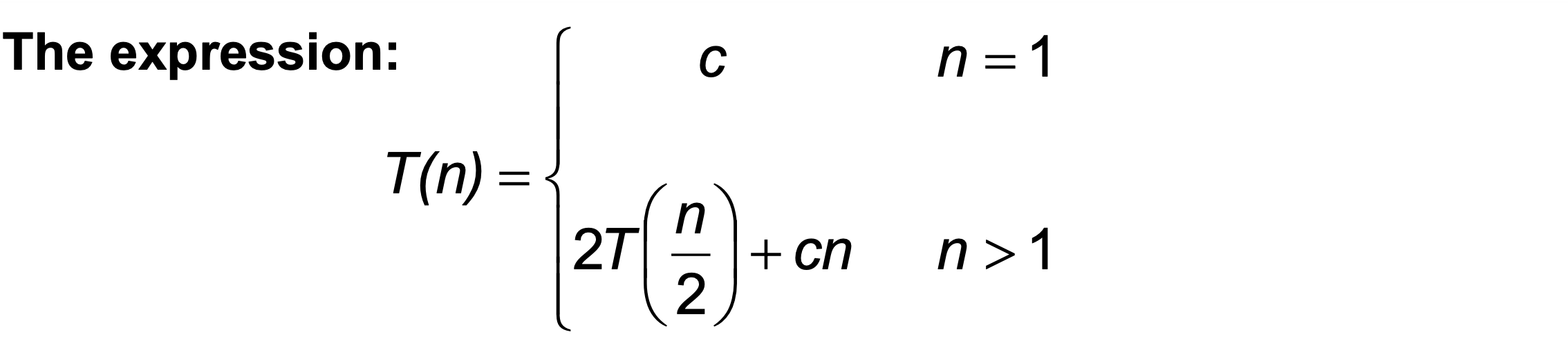

is a recurrence.

• Recurrence: an equation that describes a function in terms of its value on smaller functions

Solving Recurrence Equations

Substitution(치환) method

by mathematical induction

Recursion-tree method

• Build a recursion tree.
  - Each node is the cost of a single subproblem.
• Sum the costs within each level.
• Sum the costs of all levels.

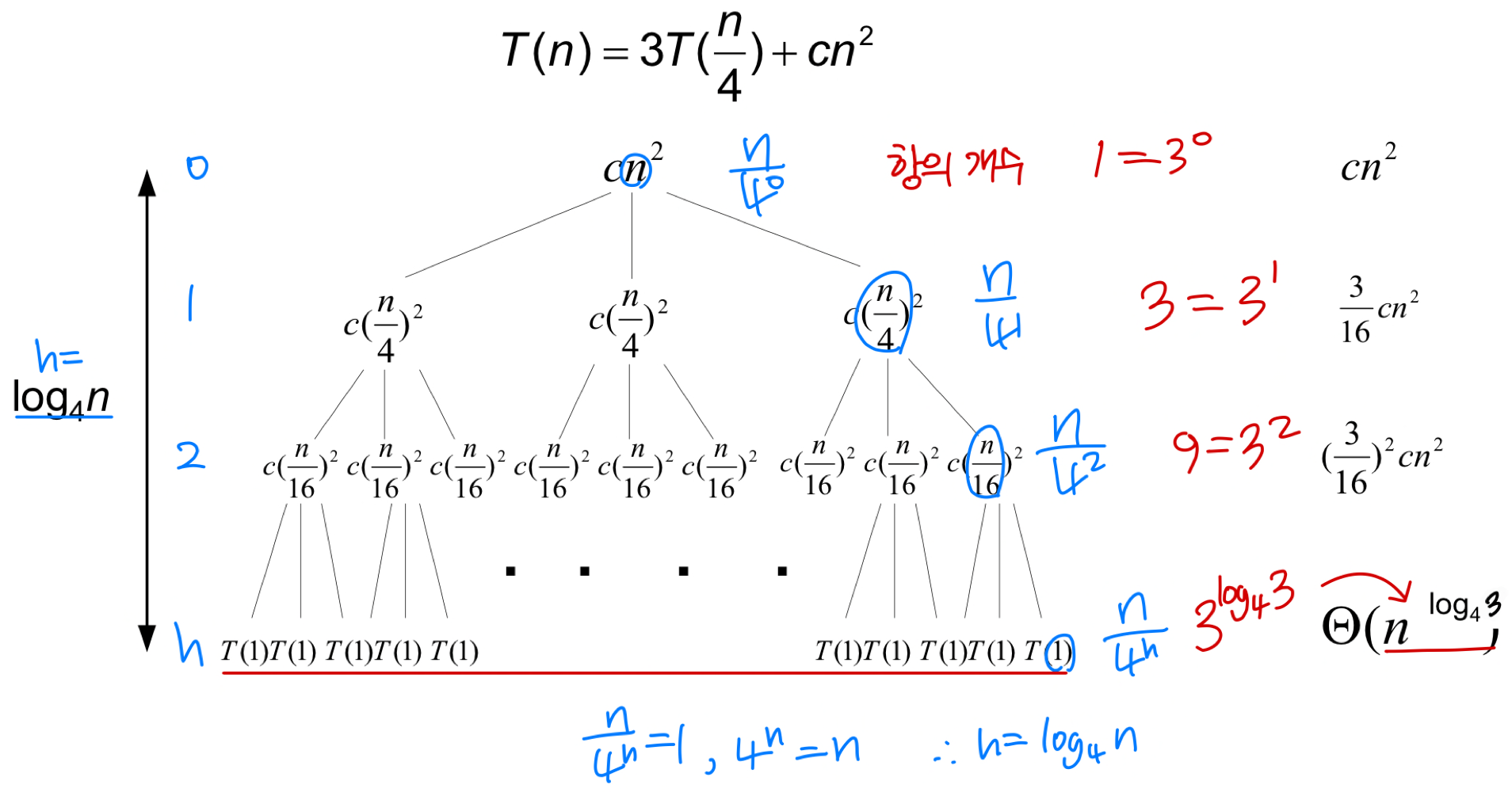
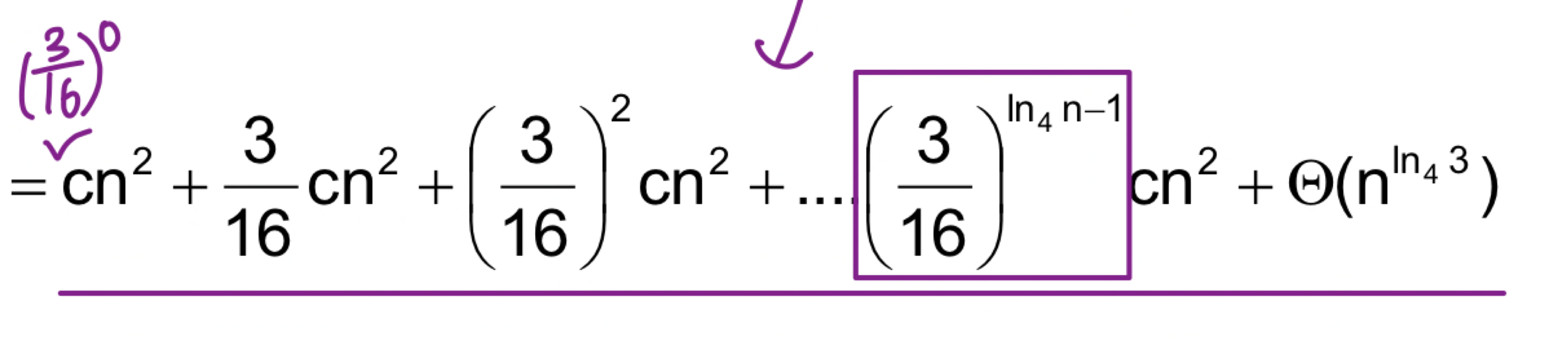
Example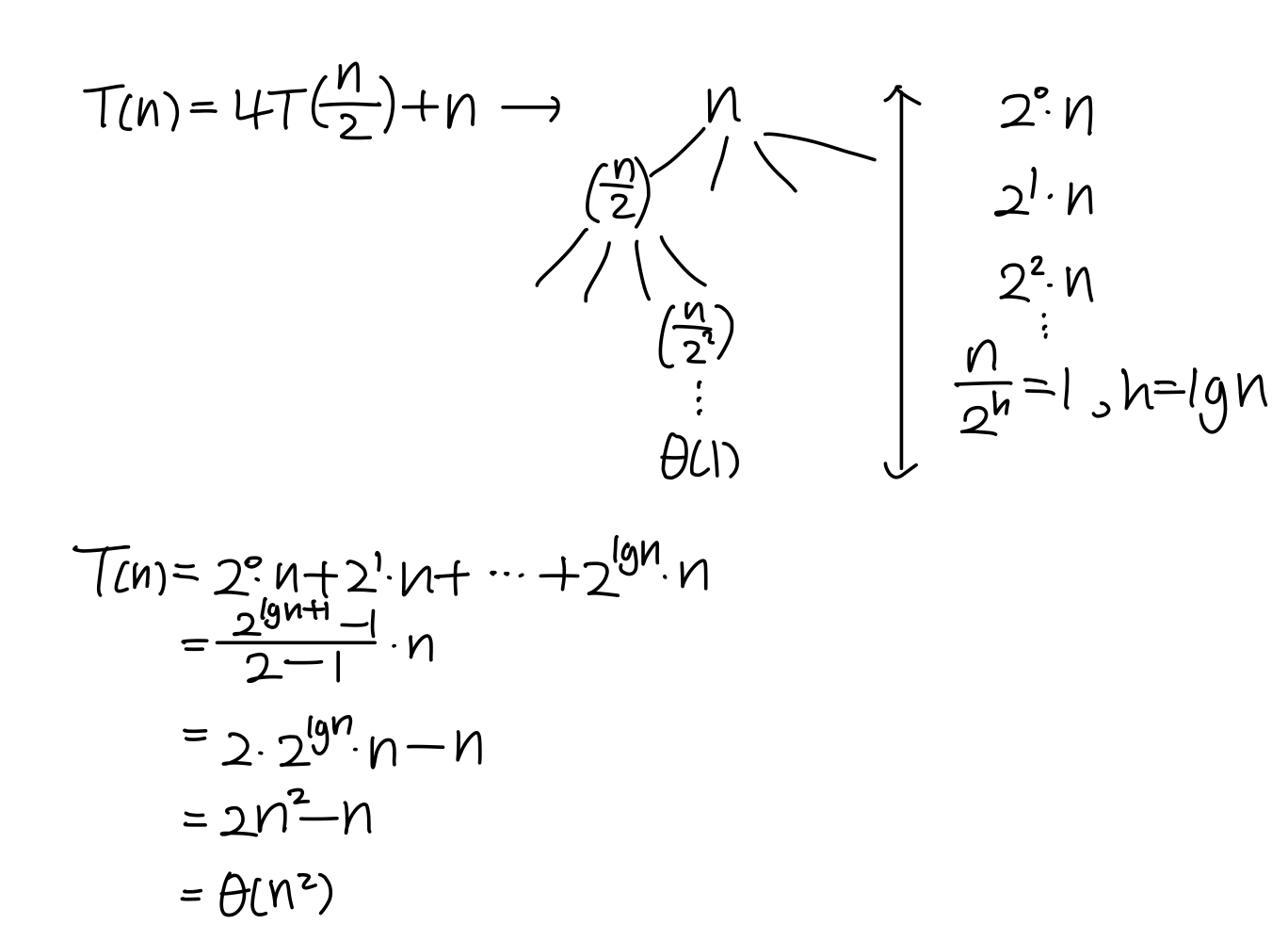

Iteration Method

Example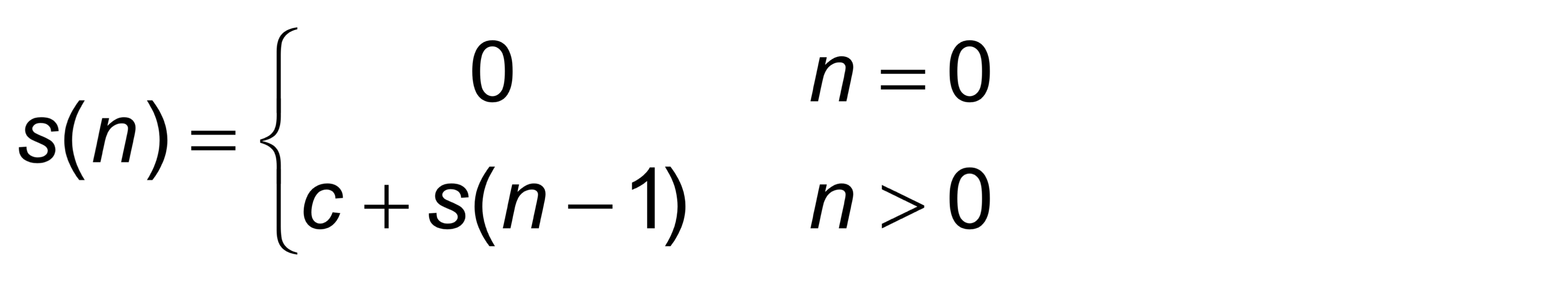

• So far for n >= k we have
  - s(n) = ck + s(n-k)
• What if k = n?
  - s(n) = cn + s(0) = cn
• Thus in general
  - s(n) = cn = θ(n)

Another method (similar)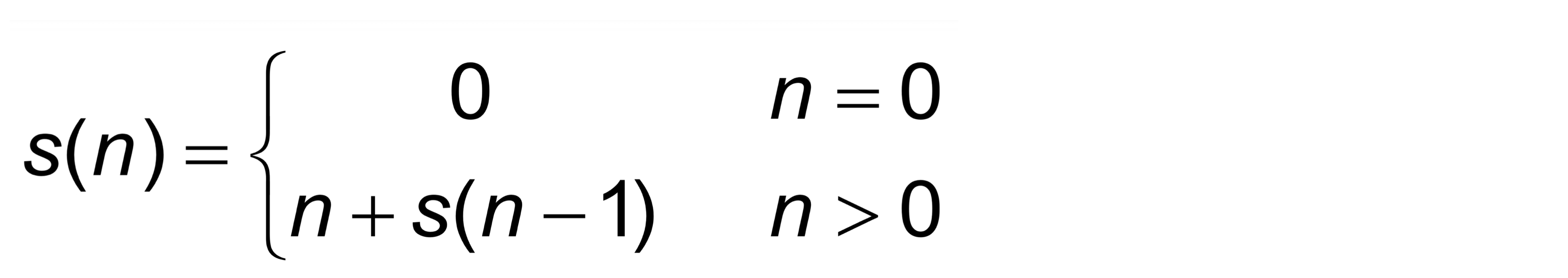

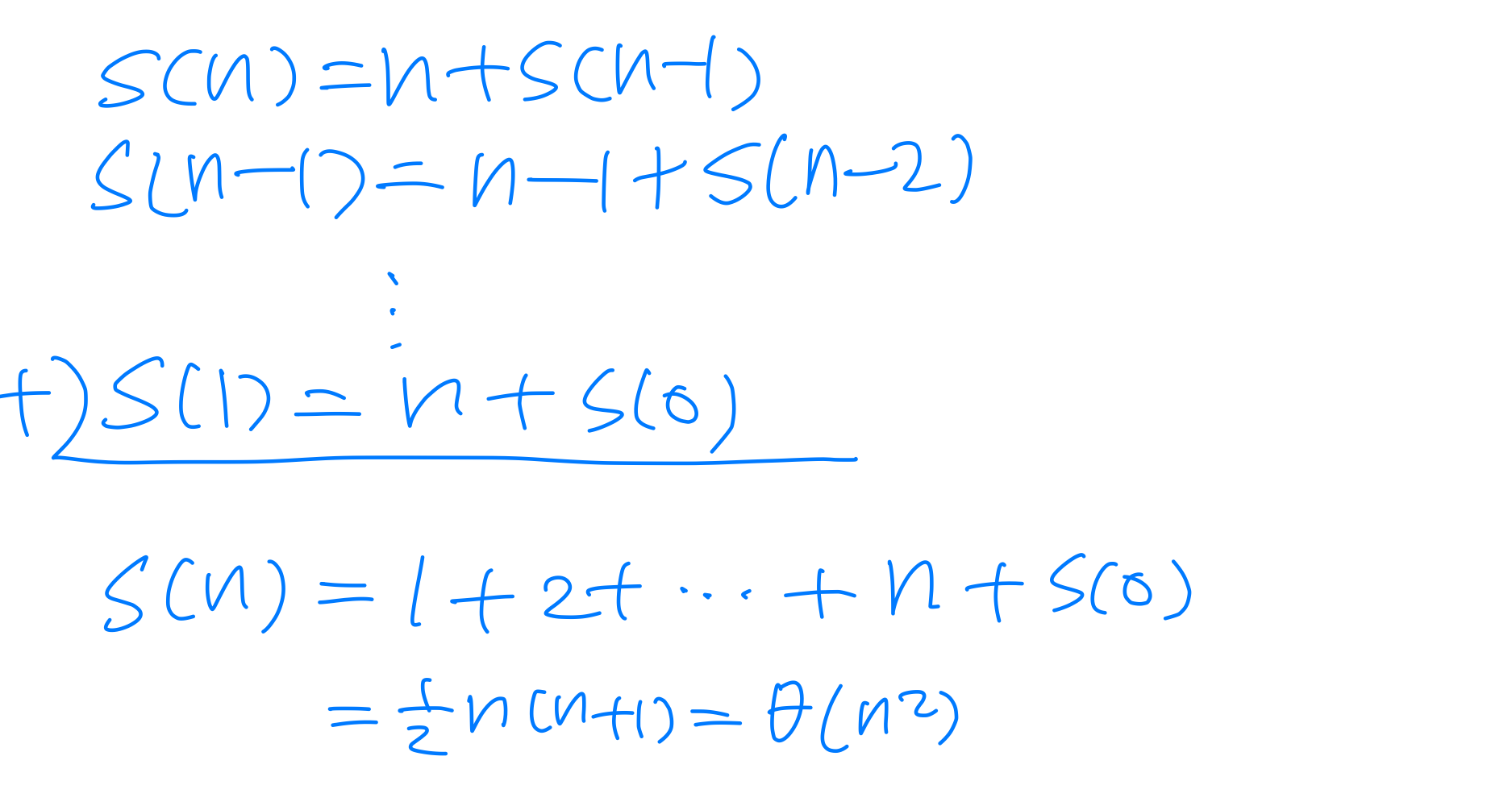
Master method

Example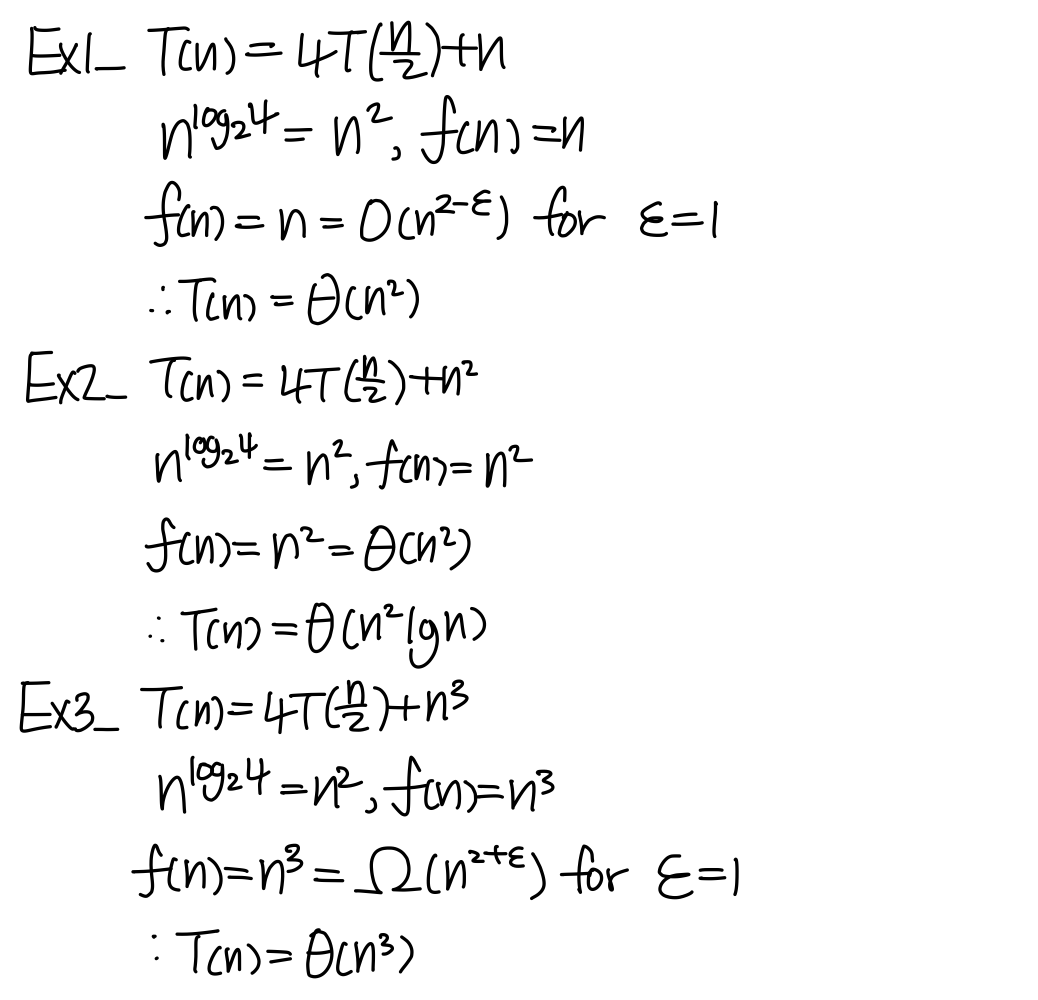

Proof By Induction

• Base case: n=0 or n=1
  - Show formula is true when n = 0 or 1
• Inductive hypothesis:
  - For n greater than 0, assume that the formula holds true for all k ≥ 0 such that k < n
  - By inductive hypothesis, the formula is true when k = n - 1 ( or n / 2 )
• Proof of goal statement:
  - Show that formula is then true for n

⭐️ No such thing as 'n + 1'

Example

Exercise

Ex1_ Matrix multiplication : Iterative solution

Determine time complexity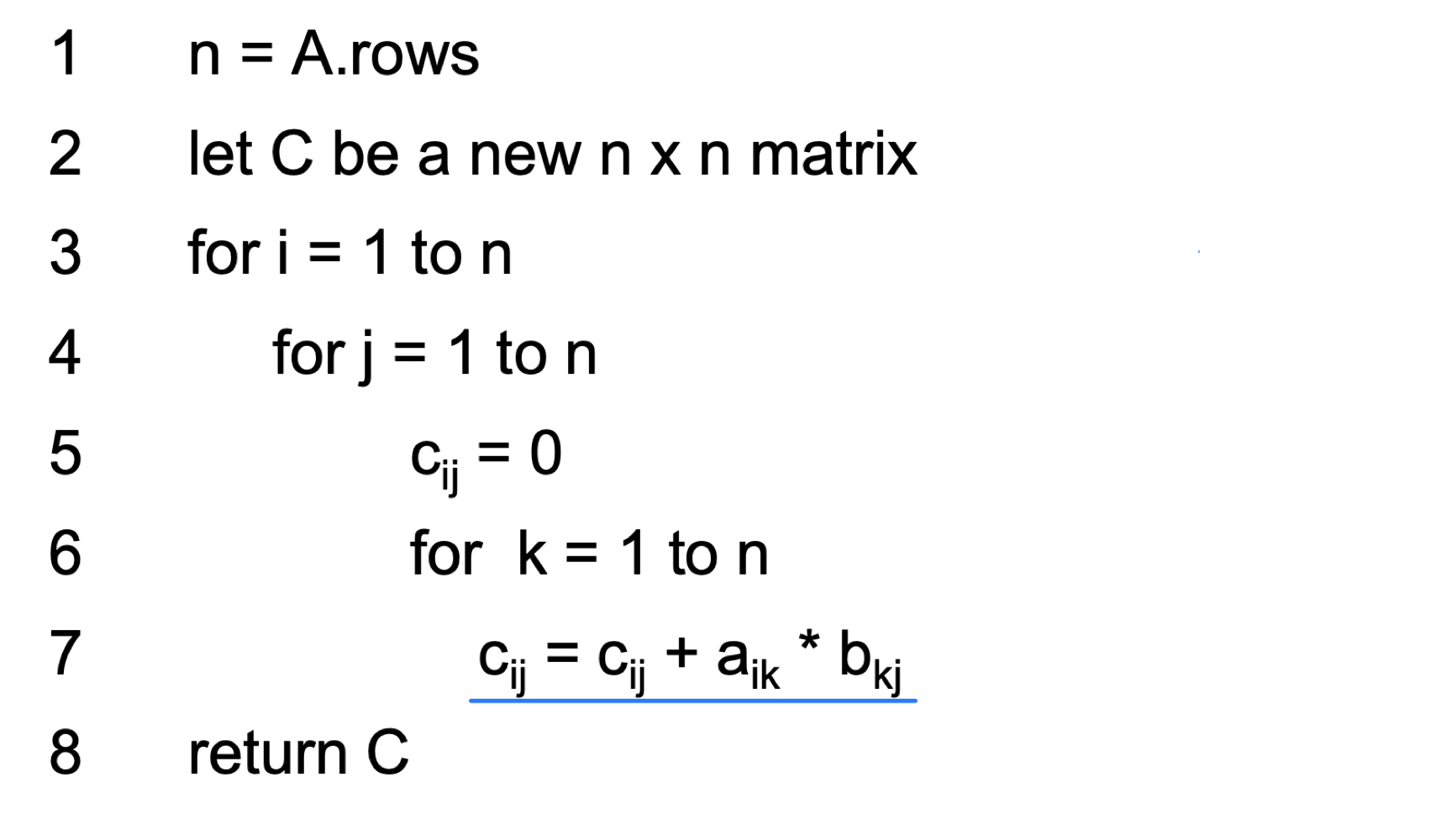➡️ θ($n^3$)

Ex2_ Matrix multiplication : Divide-and-Conquer (Recursive)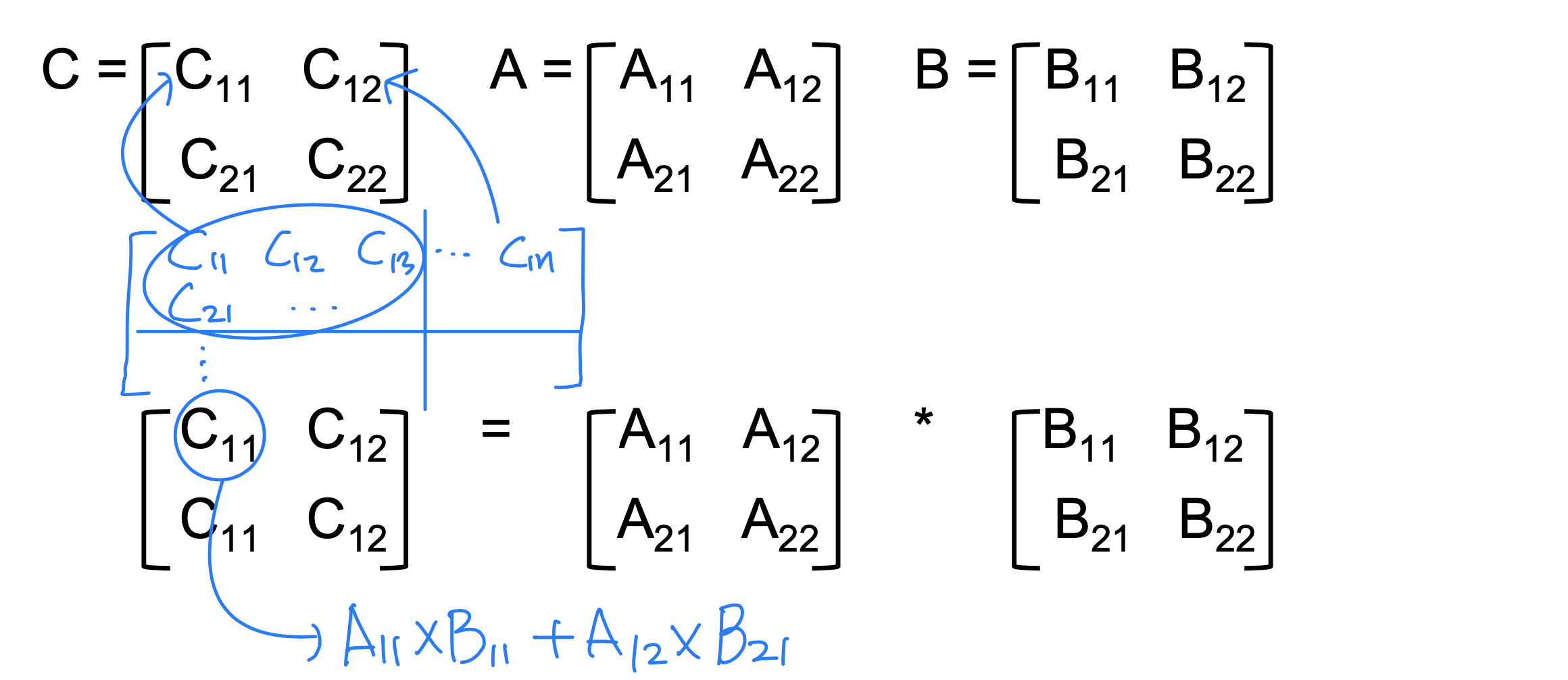

Q1. Express time complexity T(n) of divide-and-conquer algorithm as recurrence equation
➡️

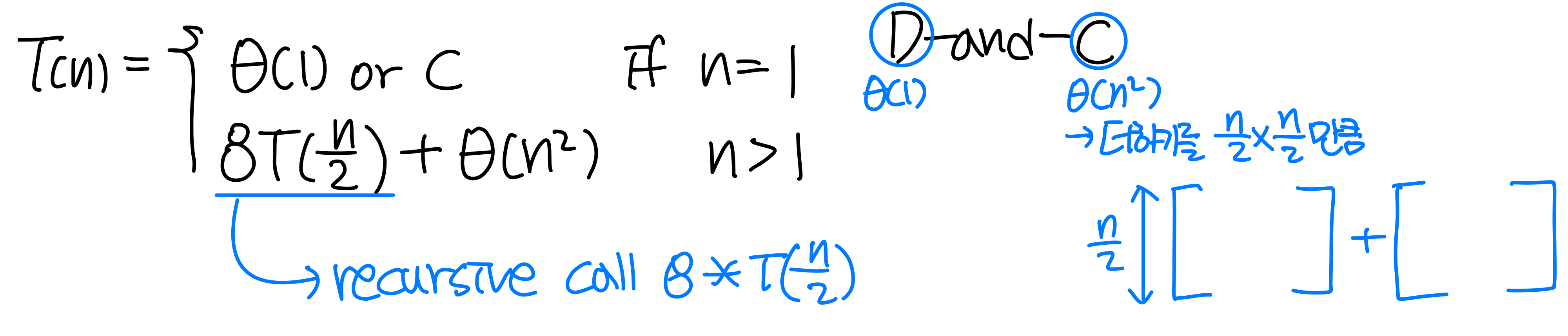
Q2. Solve equation with Recursion tree method
➡️

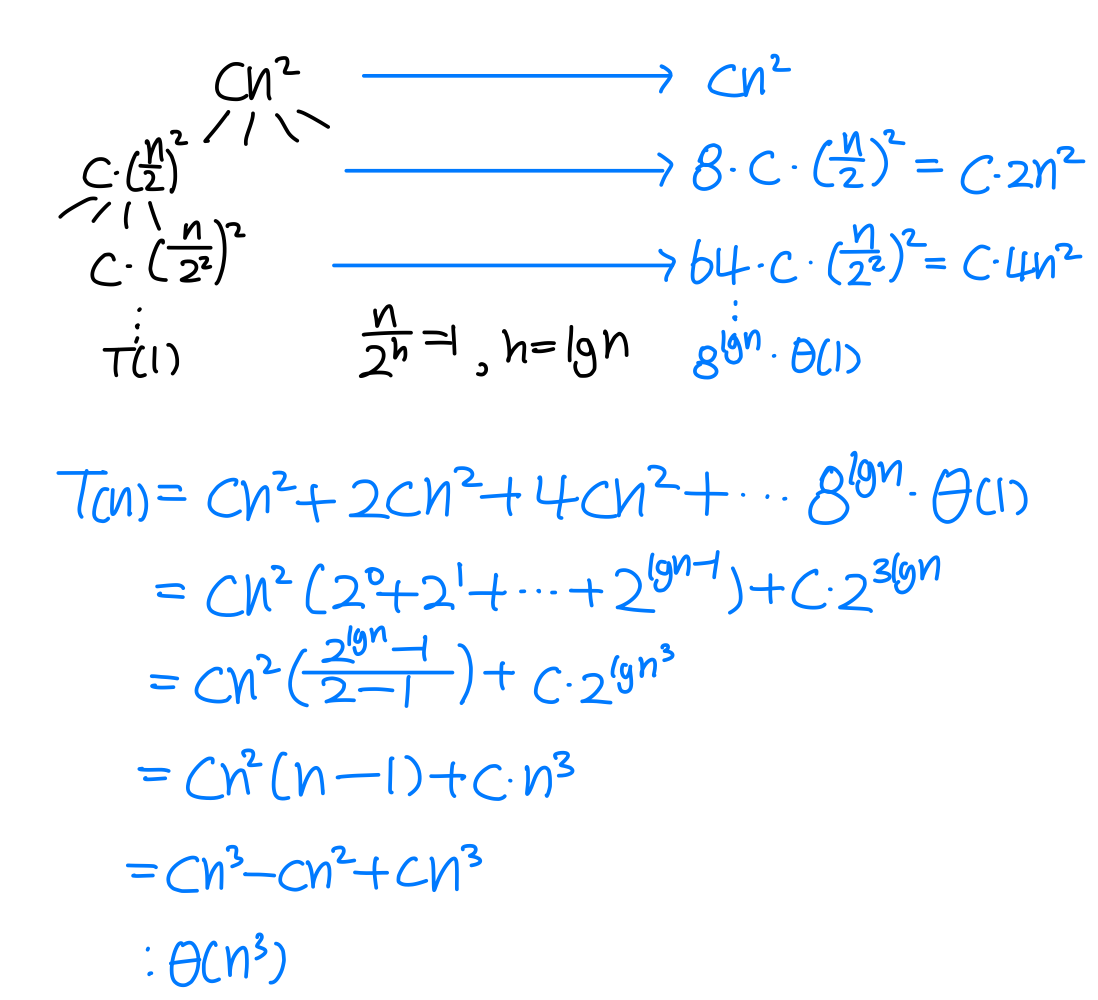
Q2. Solve equation with Master method
➡️

Exercise in class

1. Recursion Tree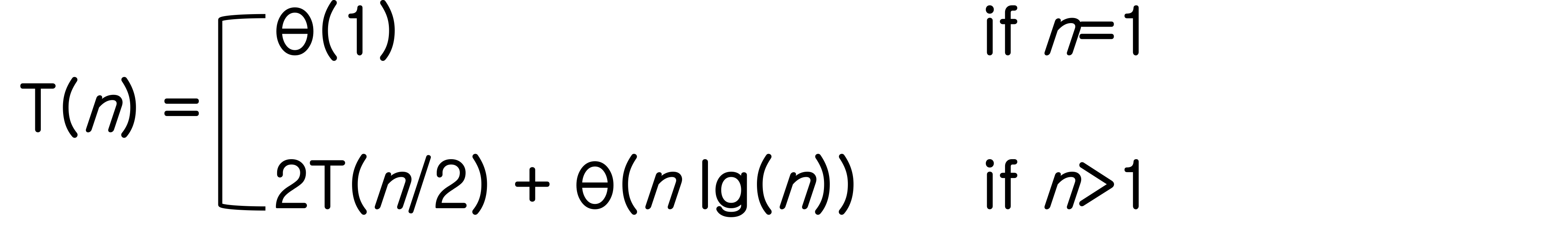

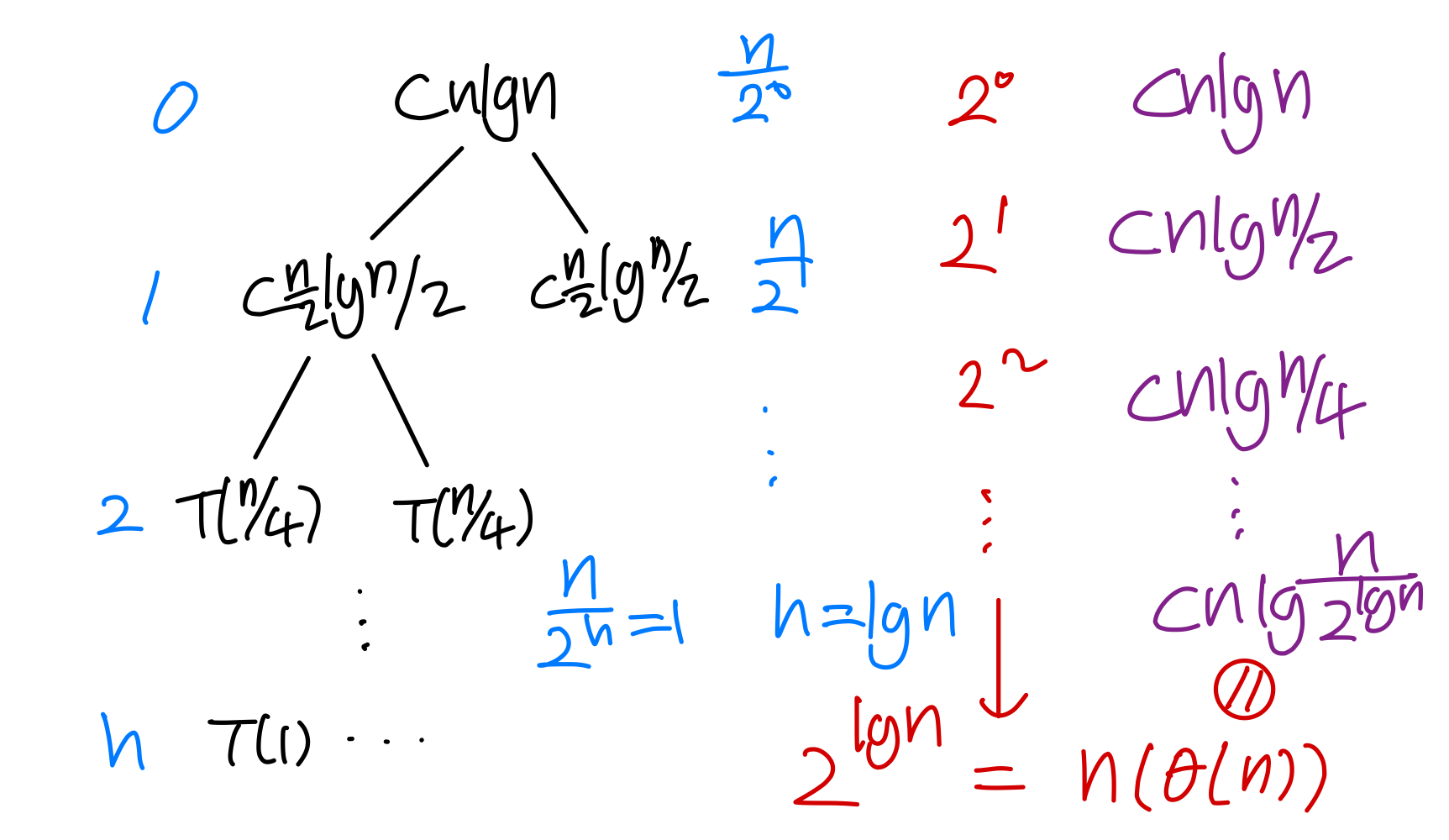
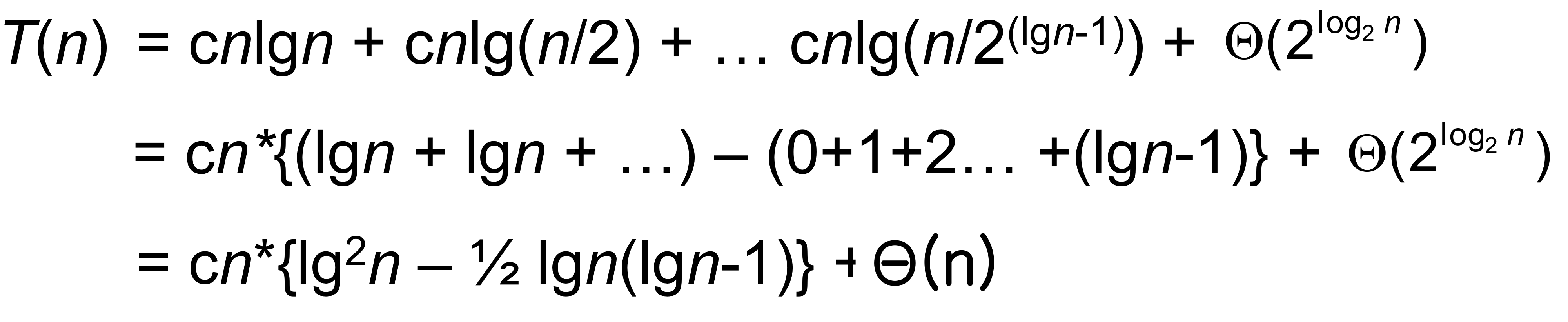
➡️ θ(n $lg^2$n)

2. Master theorem with same problem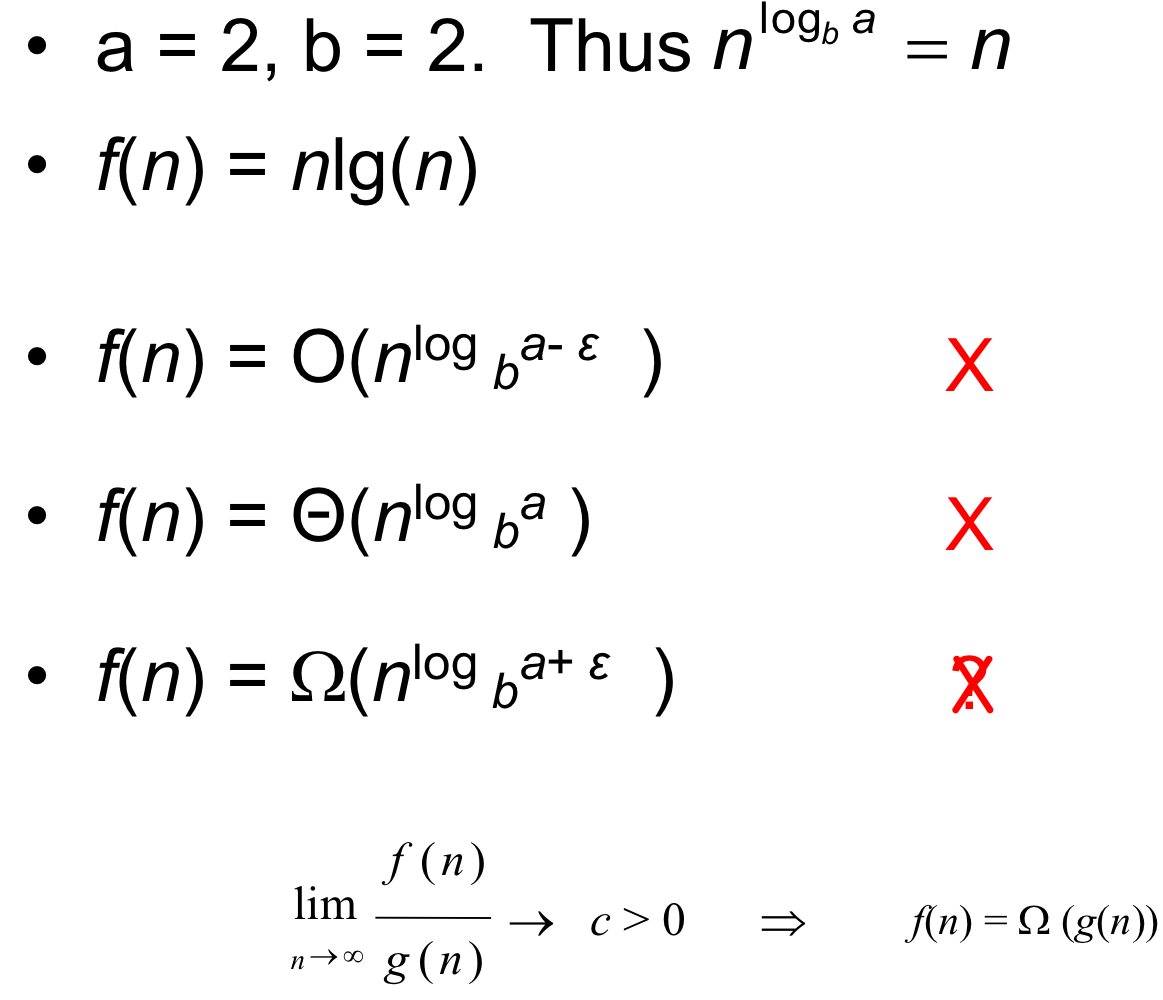

⭐️ Master theorem으로 커버못하는 부분이 있다 ➡️ Recursion tree!

3. Master theorem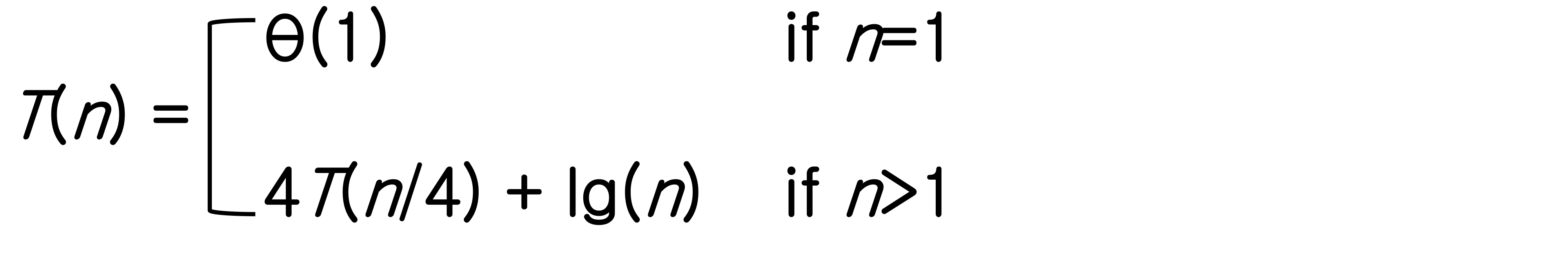

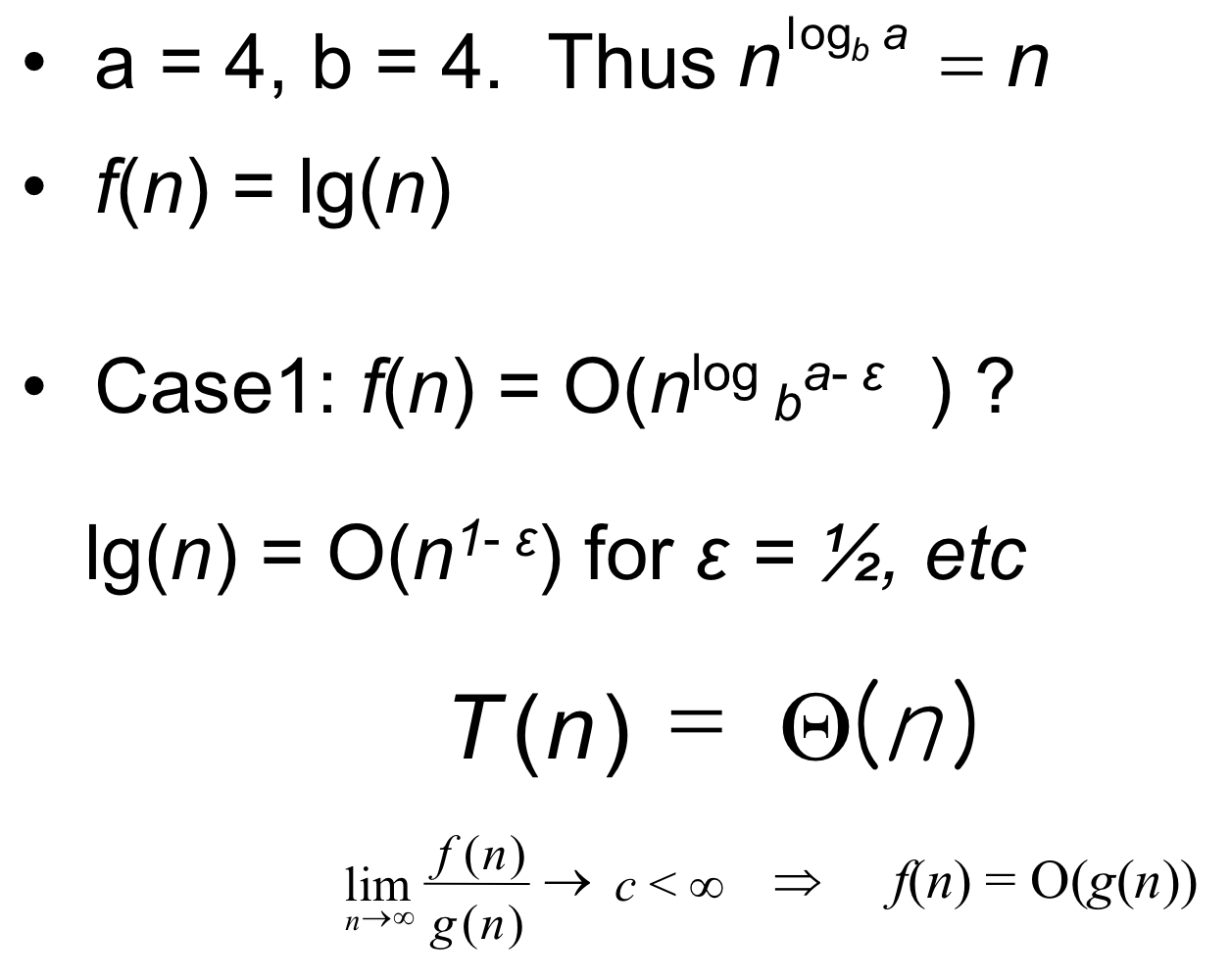
4. Proof by induction

Prove 1 + 3 + 5... + (2n-1) = $n^2$

• Base case:
  - When n = 1,then $1^2$ = 1
• Inductive hypothesis:
  - For n greater than 0,assume that 1 + 3 + 5 ... + (2k - 1) = $k^2$ holds true all k ≥ 0 such that k < n
  - By hypothesis the formula is true when k = n - 1,
  1 + 3 + 5... + (2n - 3) = $(n - 1)^2$
• Proof of goal statement:
  - 1 + 3 + 5... + (2n-3) + (2n-1) = $(n-1)^2$ + (2n-1) = $n^2$

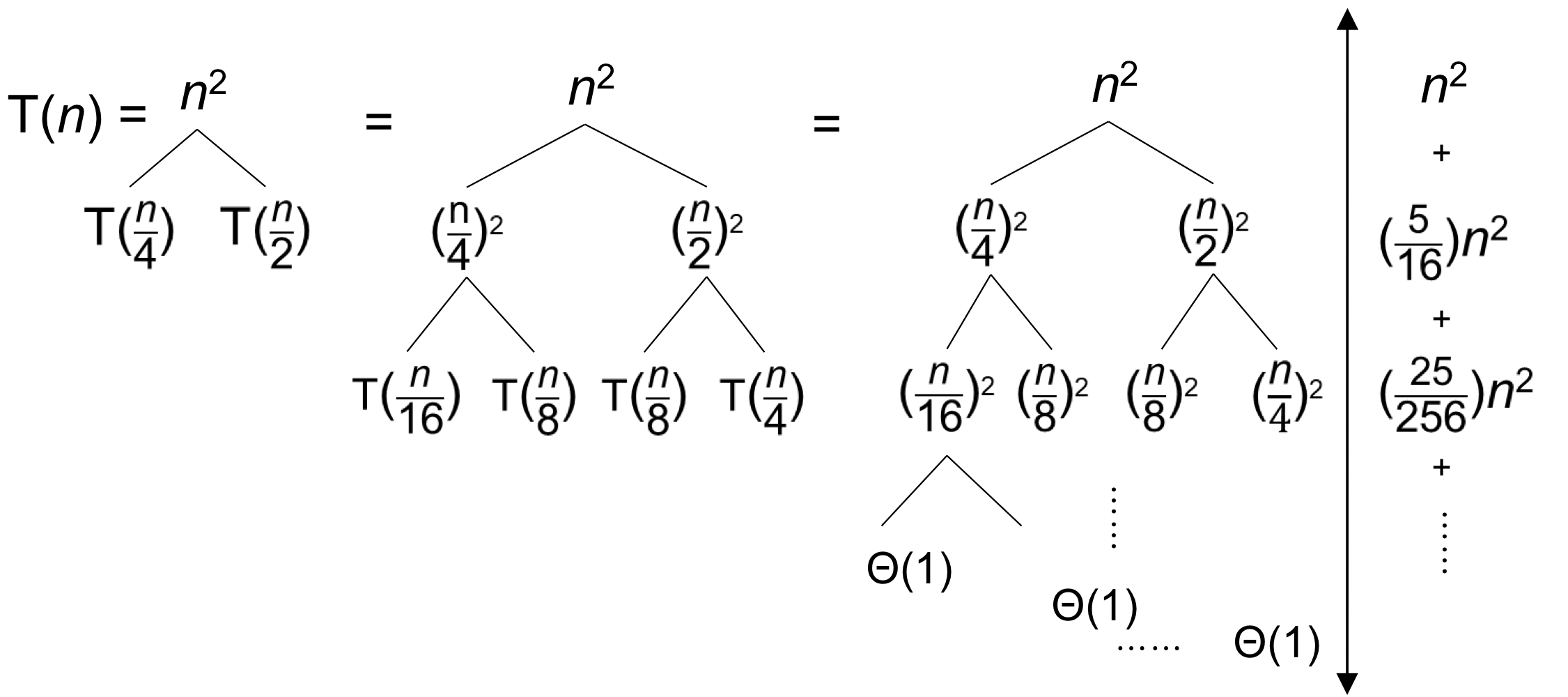
5. ⭐️ Recursion tree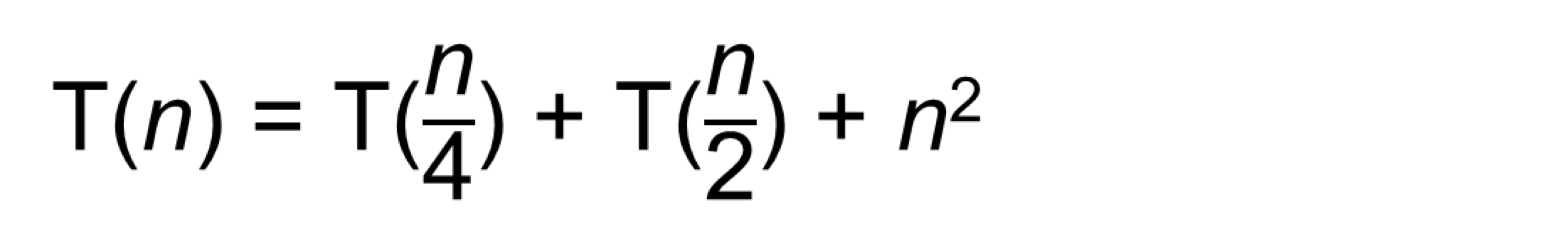

⭐️ 6. Fibonacci

1) Express the time complexity T(n) of this algorithm as a recurrence equation.
Divide : θ(1), Combine : θ(1)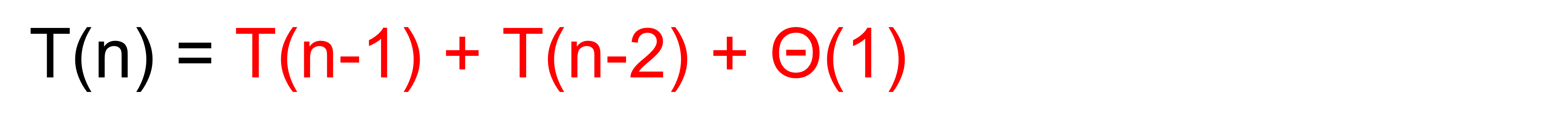

2) What is the running time (lower/upper bound) of this algorithm?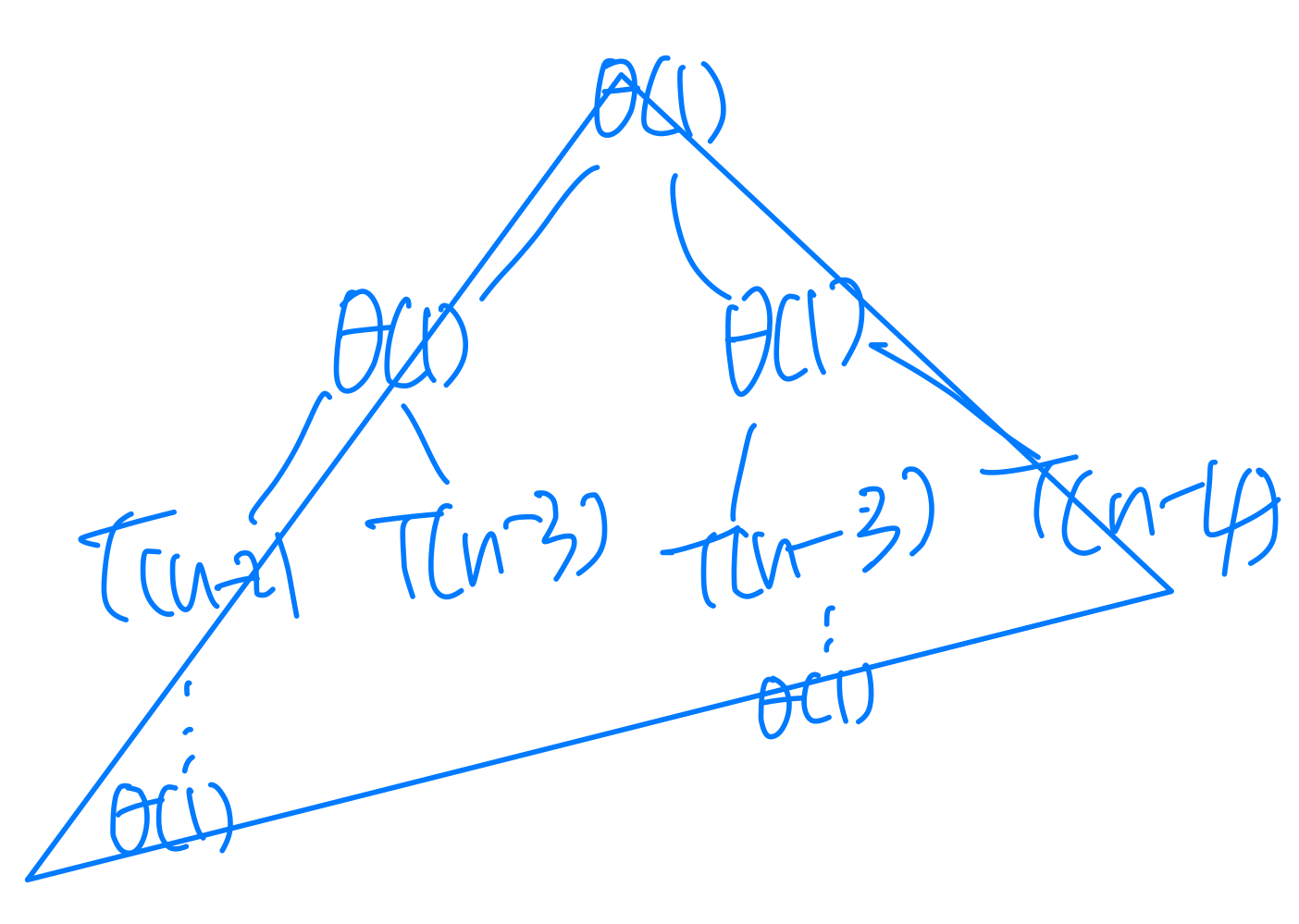

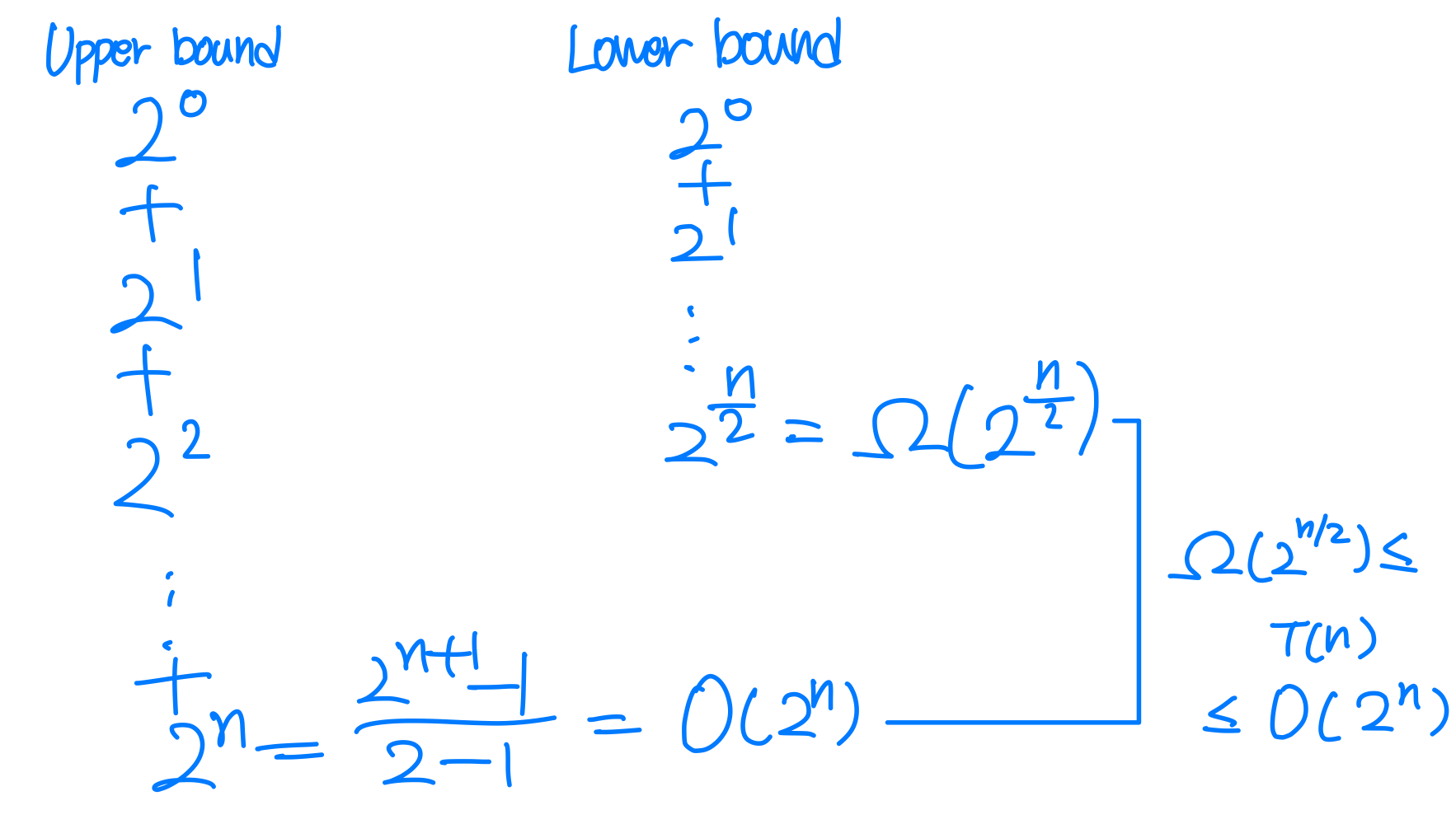
⭐️ 7. Master theorem 1, 2, 3 모두 해당하지 않을 때

$f(n) = \Theta(n^{log_ba}lg^kn)$ when $k>=0$
➡️ $T(n) = \Theta(n^{log_ba}lg^{k+1}n)$

HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.