: Not a specific algorithm, but a design paradigm(strategy)
- Used for optimization(making choice) problems:
– Find a solution with the optimal value
– Minimization or maximization
Ex_ Shortest-path, Job scheduling - S = combine( S1, S2, ..., Sm ) ➡️ smaller problem
- D and C와 비슷하지만 bottom-up fashion
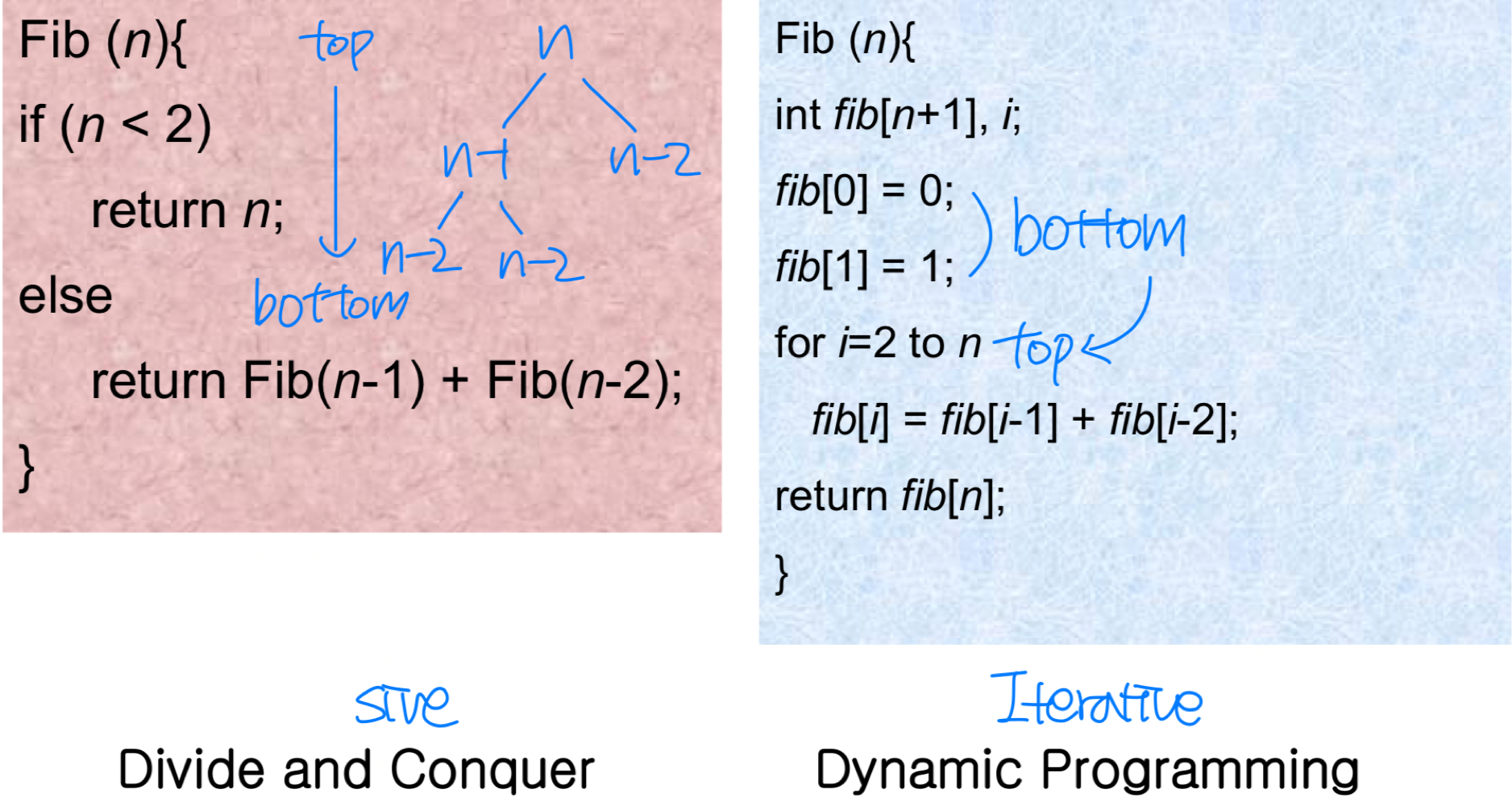
- D and C와 비슷하지만 bottom-up fashion
Divide and Conquer vs. DP
A divide-and-conquer algorithm may do more work than necessary, repeatedly solving the common subproblems. A dynamic-programming algorithm solves every subproblem just once and then saves its answer in a table, thereby avoiding the work of recomputing the answer every time the subproblem is encountered. Dynamic programming is typically applied to optimization problems.
Matrix Multiplication
parenthesizing
- Given a p × q matrix A and a q × r matrix B, their product is a p × r matrix C defined by
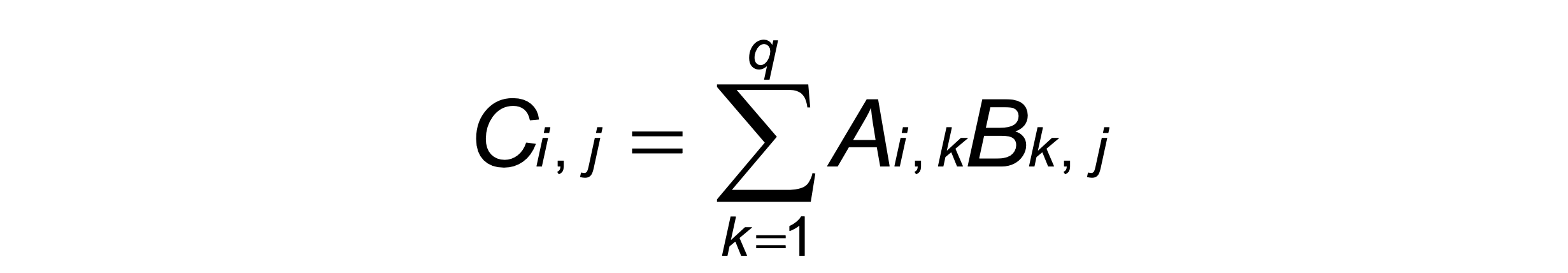
- The cost of computing C is p · q · r
- Given three matrices:
A = p × q matrix
B = q × r matrix
C = r × s matrix
- Two ways : ( A · B ) · C or A · ( B · C )
- first p · q · r + p · r · s = p · r · ( q + s )
- second q · r · s + p · q · s = ( p + r ) · q · s - The ways of parenthesizing make a rather dramatic difference
Ex_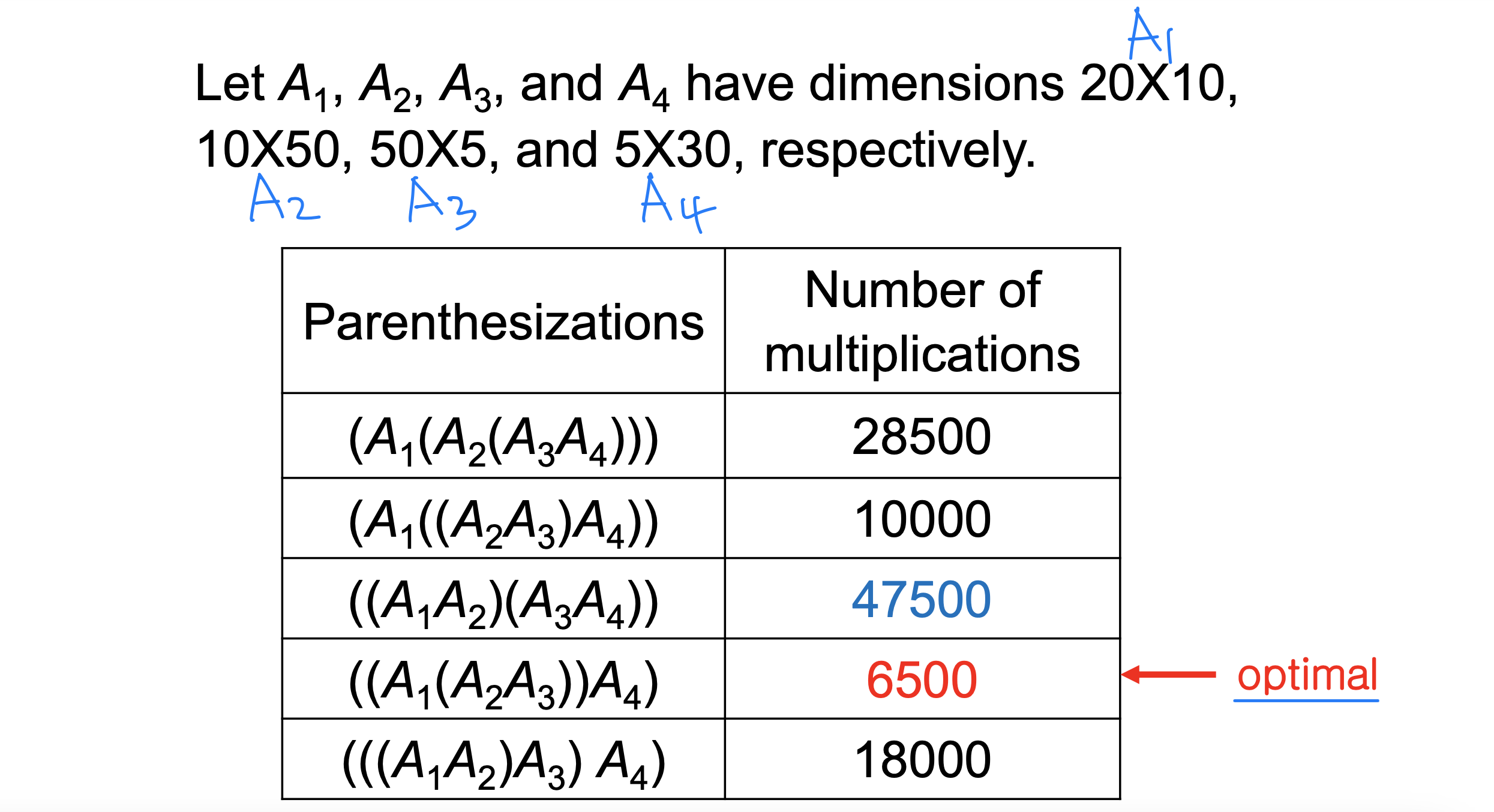

 ➡️ brute-forece로 어떻게 곱하는지는 의미가 없다. 답은 DP
➡️ brute-forece로 어떻게 곱하는지는 의미가 없다. 답은 DP
왜 이렇게 오래걸릴까? Recalculation!!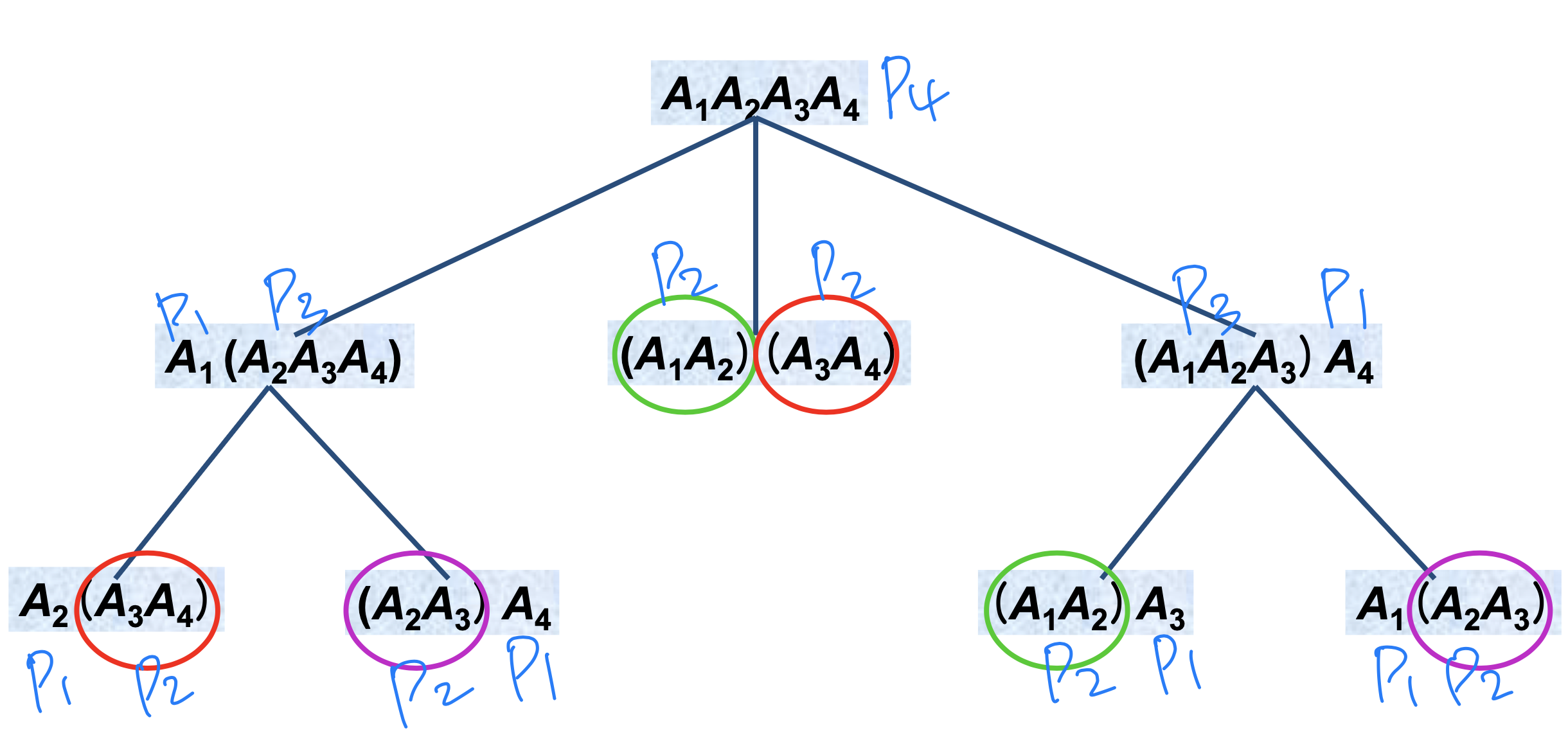
Structure of Optimal Solution
- Key Observation : Given optimal sequence A A .... A, suppose the sequence is split between A and A. Then the sequence A ... A, and A ... A are optimal ➡️ (A ... A), (A ... A) 각각 optimal
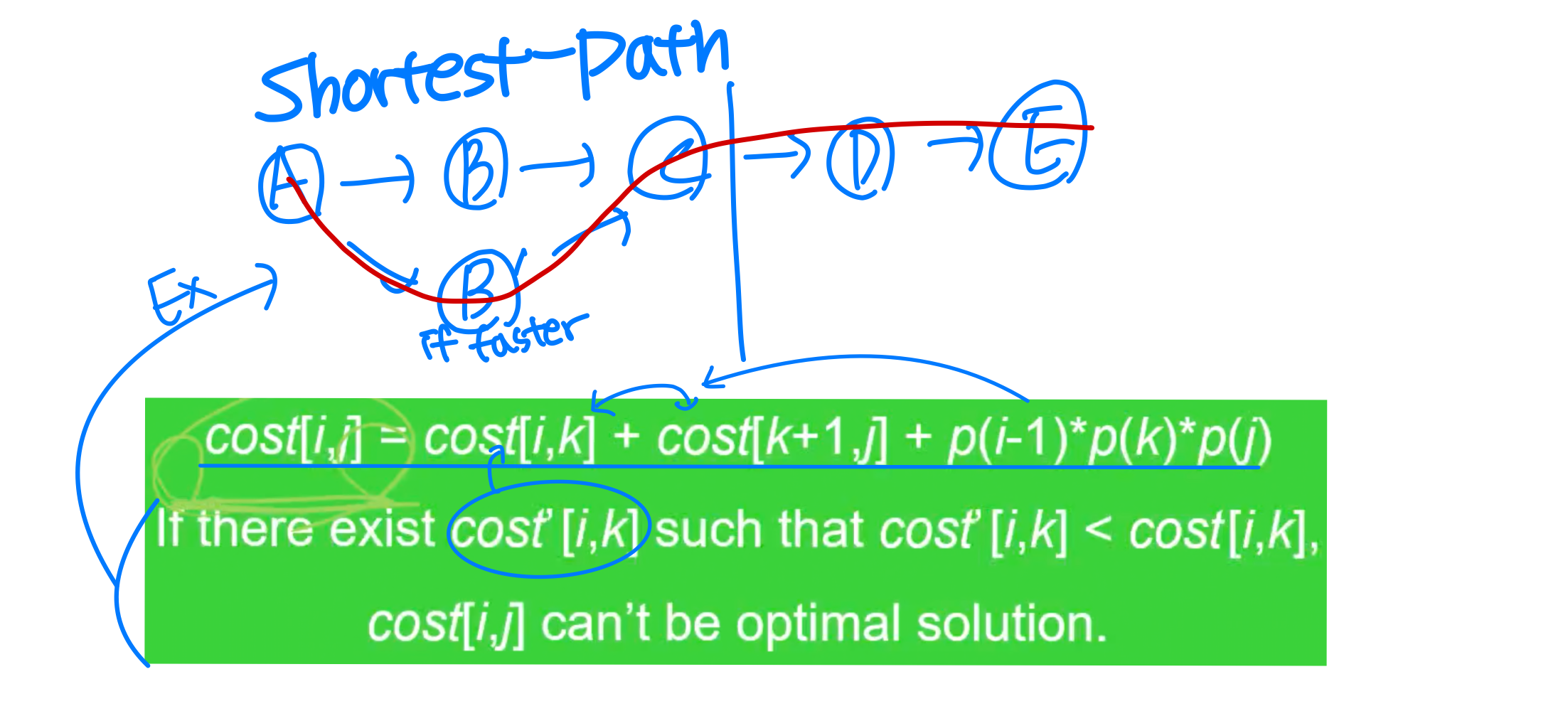
- Optimal Substructure: An optimal solution to an instance contains within it optimal solutions to smaller instances of the same problem.
- Optimal Overlapping Subproblems: A recursive solution to the problem solves certain smaller instances of the same problem over and over again, rather than new subproblems.
- Principle of Optimality
- Given an optimization problem and an associated function combine, the Principle of Optimality holds if the following is always true:
➡️ Optimal Substruct.가 있을 때
Memoization
: DP approach while maintaing top-down strategy ➡️ Avoiding recaculation ➡️ 둘다 (n)
➡️ 둘다 (n)
Optimal Substructure in MCM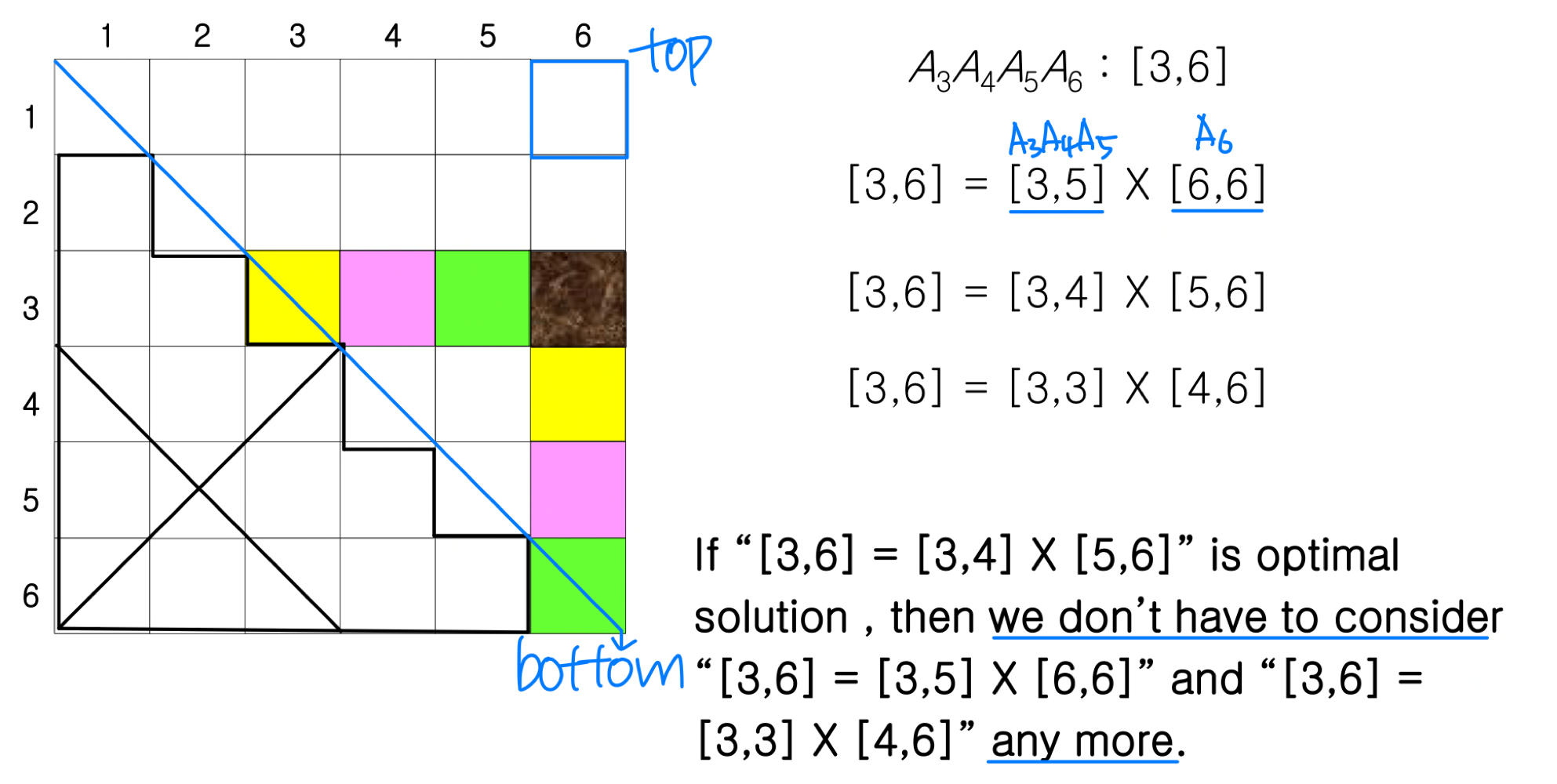
- Development of DP algorithms
- Characterize the structure of an optimal solution
- Recursively define(relation , represent to expression) the value of an optimal solution
- Compute the value of an optimal solution in a bottom-up fashion
- Construct(구성) an optimal solution from computed information
Step 1
- Find the optimal substructure
: From the key observation we identified optimal substructure. - We can build an optimal solution to an instance of the matrix-chain multiplication problem by splitting the problem into two subproblems (optimally parenthesizing AAA and AAA), finding optimal solutions to subproblem instances, and then combining these optimal subproblem solutions..
Step 2: A recursive solution
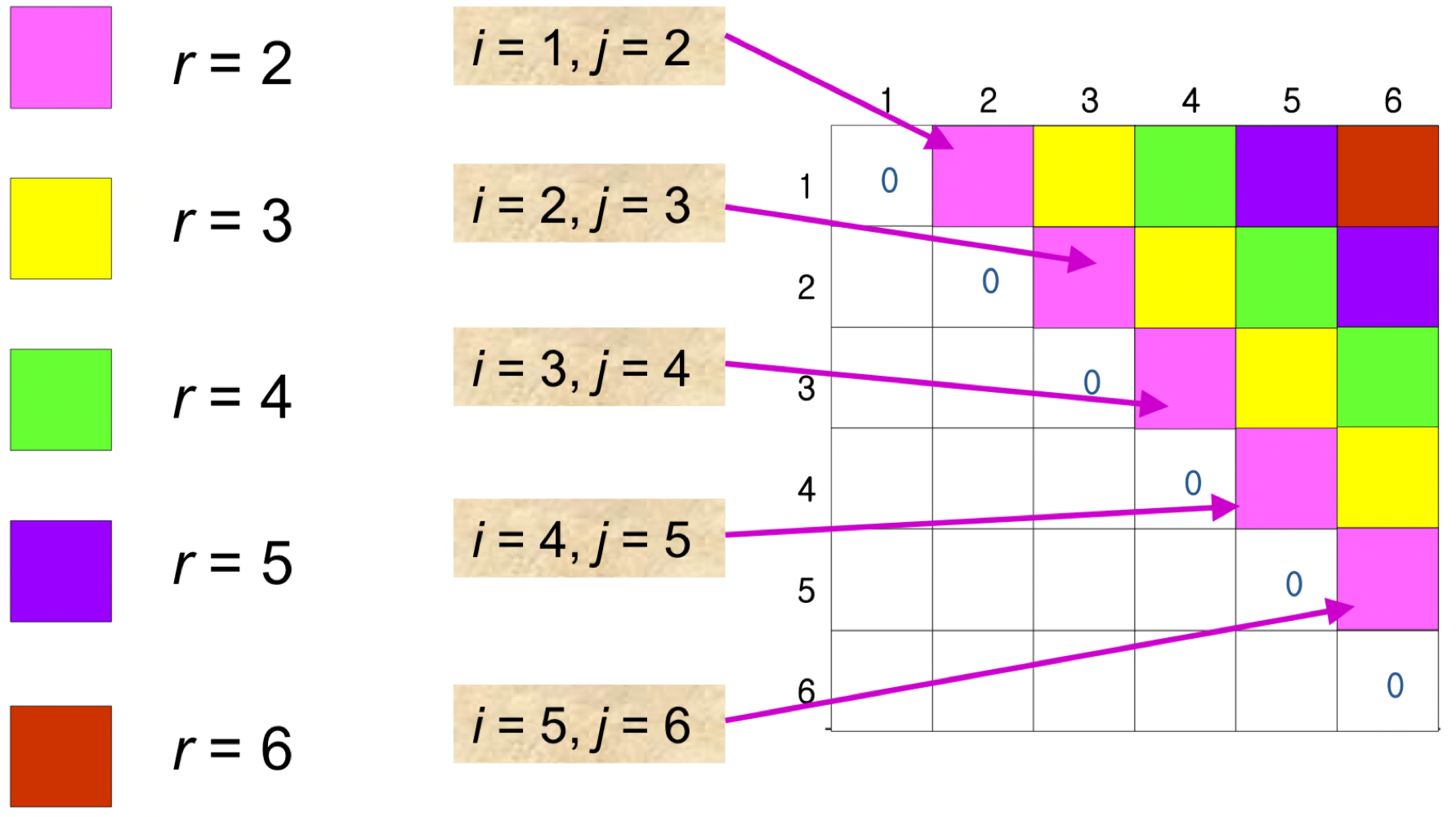
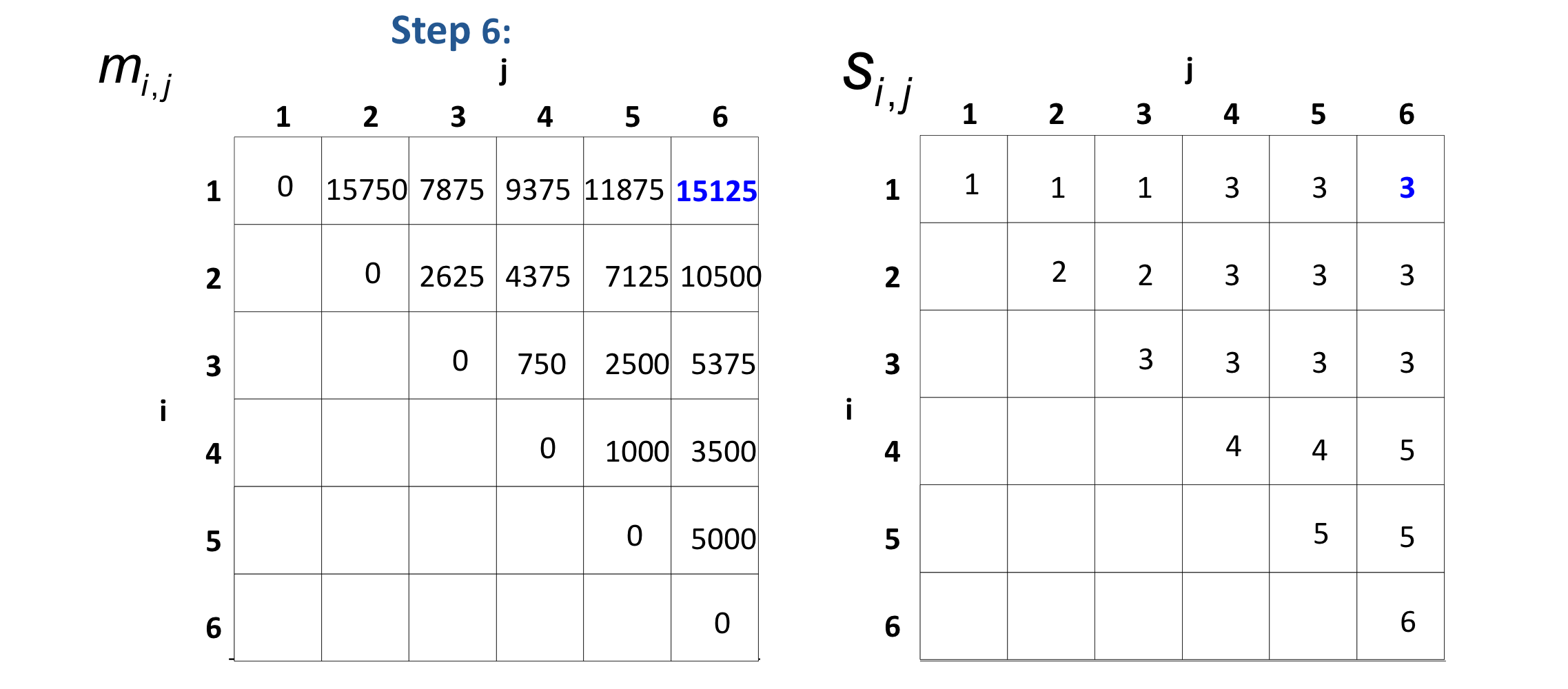
- m[i,j]: the minimum number of scalar multiplications needed to compute A ...A
- final solution: m[1,n]
- Recursively,
- if i=j, m[i,j]=0 (trivial)
- if i<j, m[i,j]=m[i,k]+m[k+1,j]+ppp for some k
Size of matrix A = pp
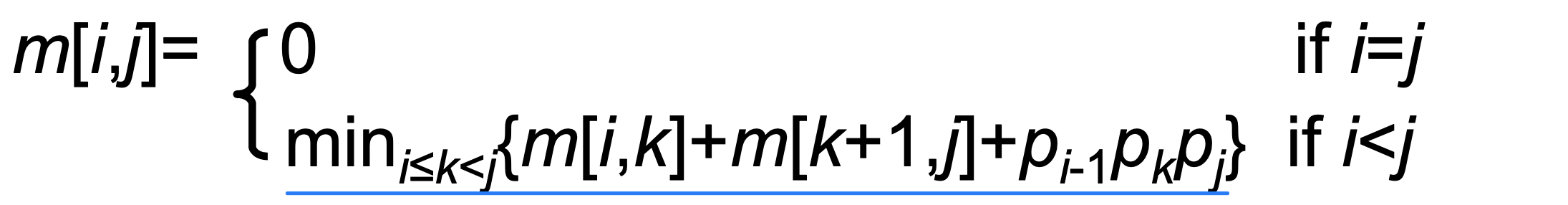
- s[i,j]: a value k

Step 3: Computing the optimal costs
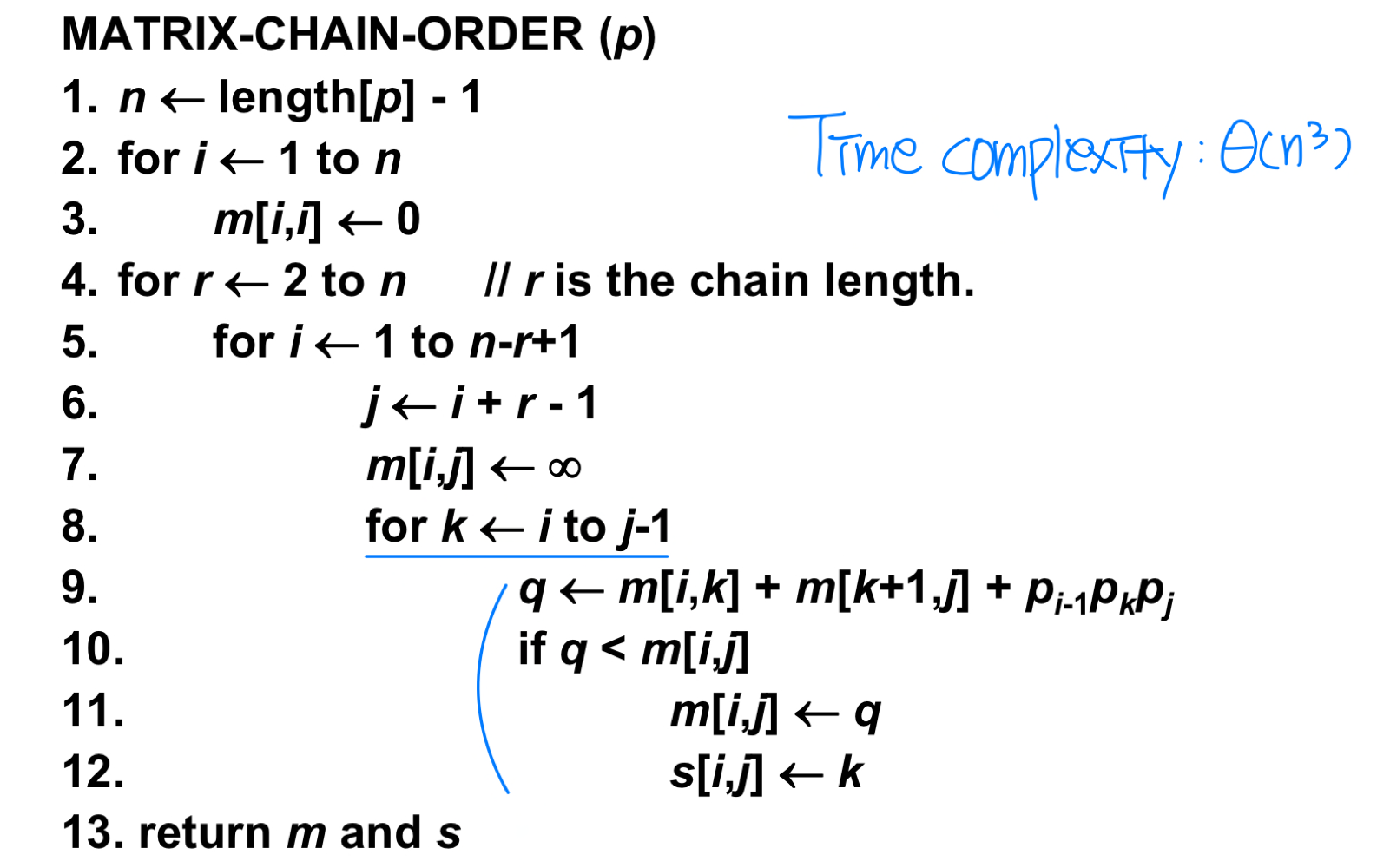

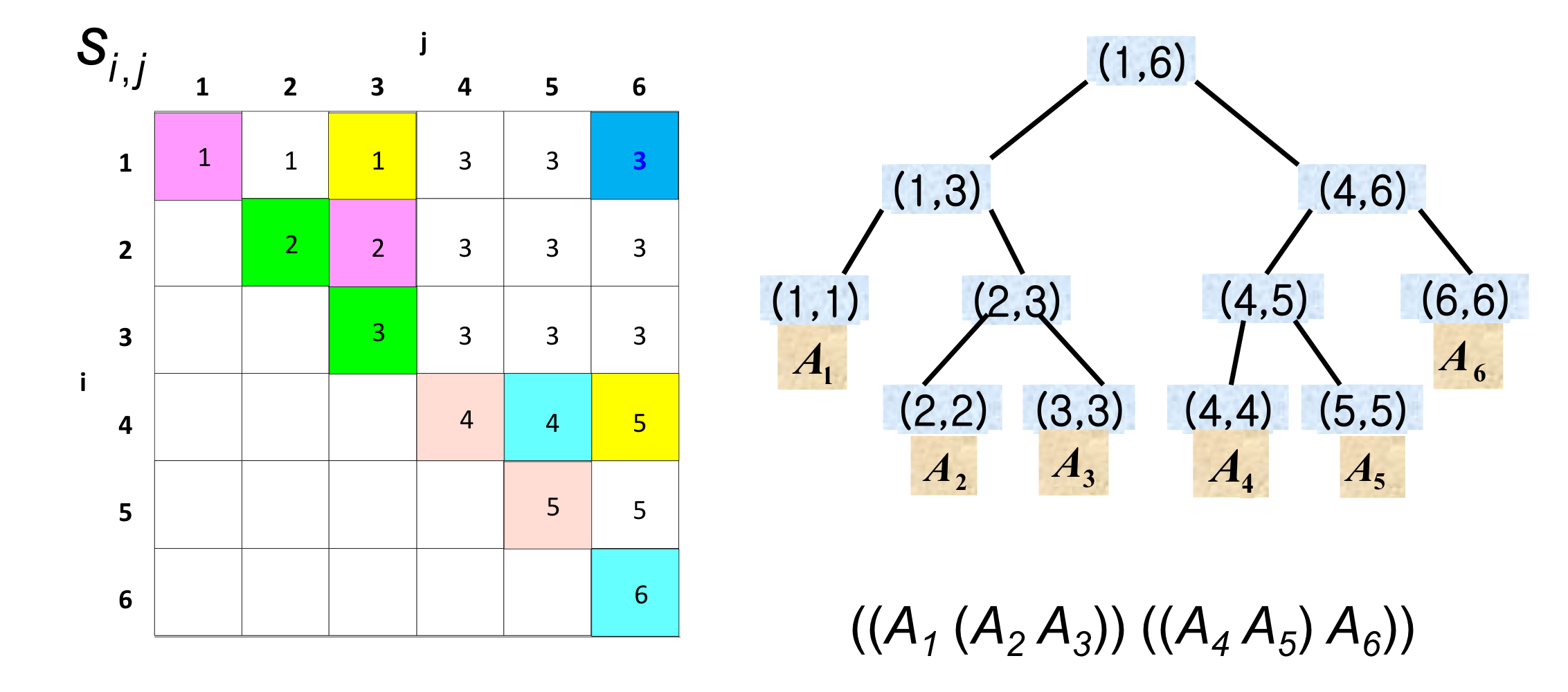
Step 4 : Constructing an optimal solution
Exercise
Exercise in class
1. T / F
Dynamic Programming is typically applied to opimization problem
➡️ T
2. DP vs. D and C
(a) How to alike?
➡️ subproblem으로 쪼개서 푸는것
(b) What is the difference?
➡️ top-down, bottom-up
(c) Which require more work?
➡️ D and C
3. What does opimal substructure mean?
➡️ An optimal solution to an instance contains within it optimal solutions to smaller instances of the same problem.
4. What does overlapping subproblem mean?
➡️ A recursive solution to the problem solves certain smaller instances of the same problem over and over again, rather than new subproblems.
5. MCM Problem
| matrix | dimesion |
|---|---|
| A | 30 x 35 |
| A | 35 x 15 |
| A | 15 x 5 |
| A | 5 x 10 |
| A | 10 x 20 |
| A | 20 x 25 |
HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.

