- A design strategy for some(every x) optimization problems.
- Make the choice that looks best at the moment.
➡️ local optimum - Not always lead to a globally optimum solutions.
- But come up with the global optimum in many cases.
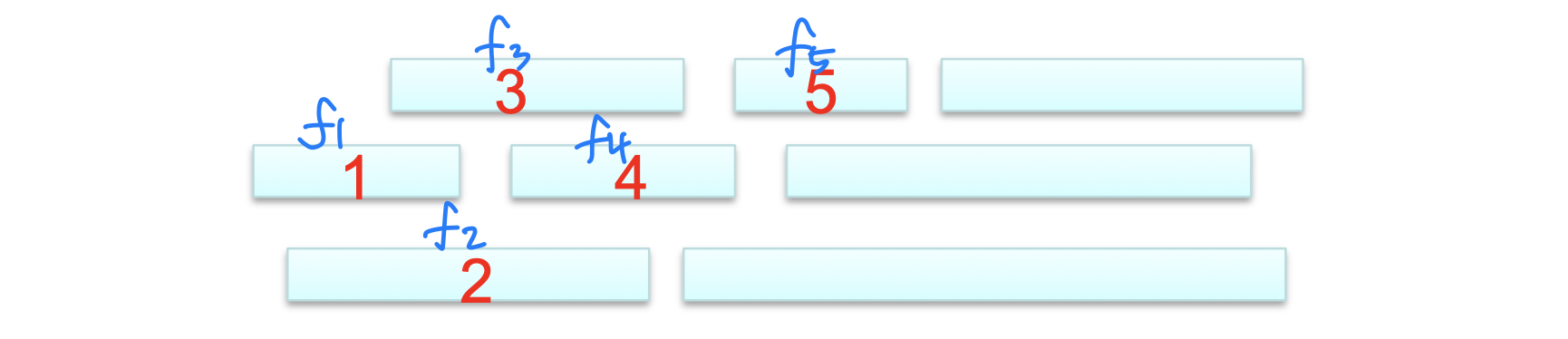
Activity Selection Problem
- Ex_ Get your money’s worth at amusement park
➡️ goal: ride as many rides as possible - We want to schedule several activities that require exclusive use of a common resource, with a goal of selecting a maximum-size set of mutually compatible activities(서로 사이좋게 지낼 수 있는)
- An activity a is represented [s,f), where s is a start time and f is a finish time.
- a and a are compatible if [s,f) and [s,f) do not overlap
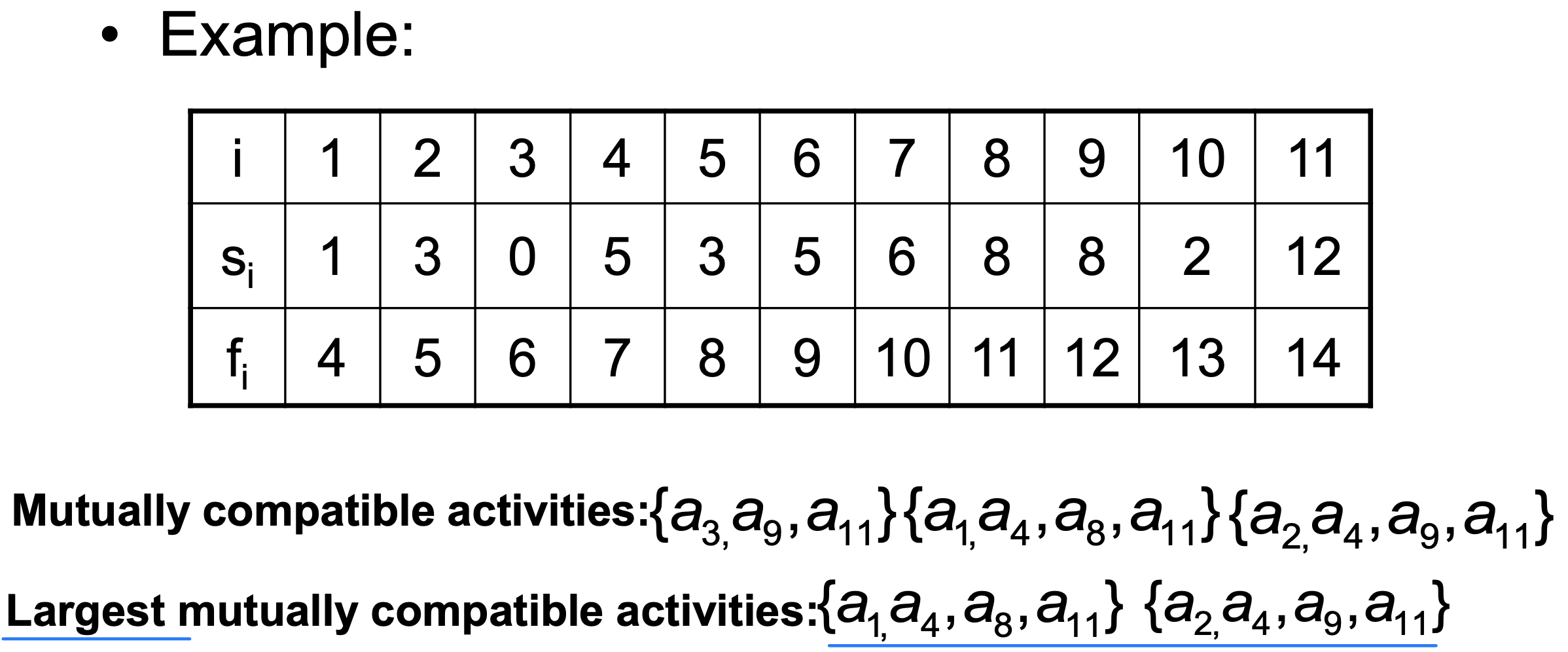
- Assume that the classes are sorted according to increasing finish times; f < f < ... < f.
The Structure of an Optimal Schedule
- the subset S begin after activity a finishes and end before activity a starts
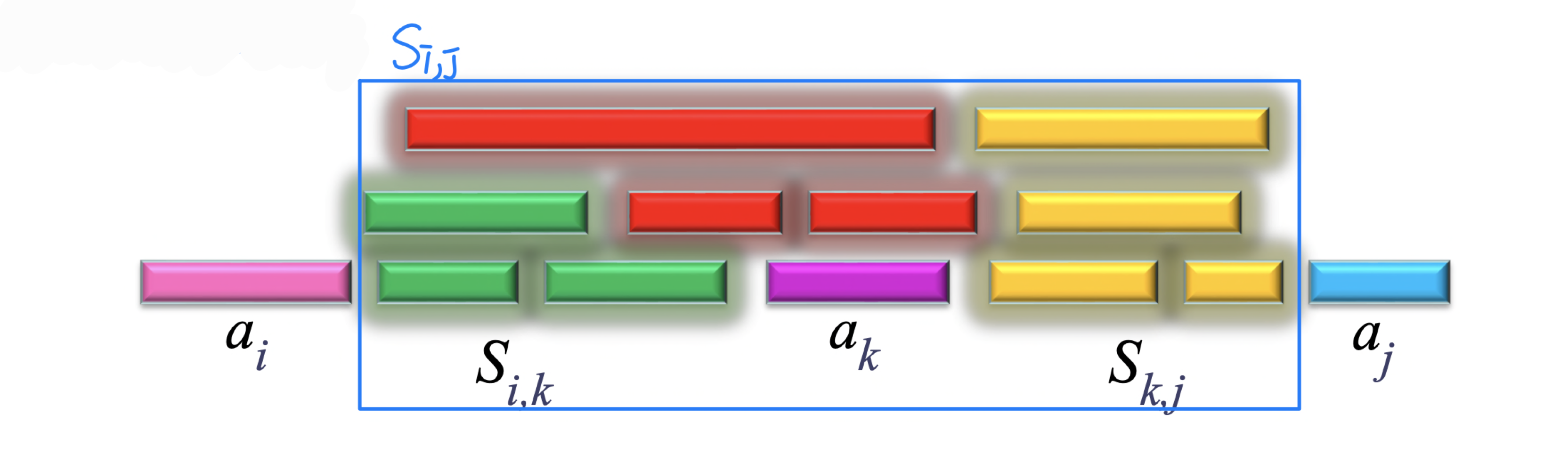
- Assume that activity a is part of an optimal schedule of the classes in S
- Then i < k < j, and the optimal schedule consists of a maximal subset of S, {a}, and a maximal subset of S
➡️ Optimal substructure? Yes.
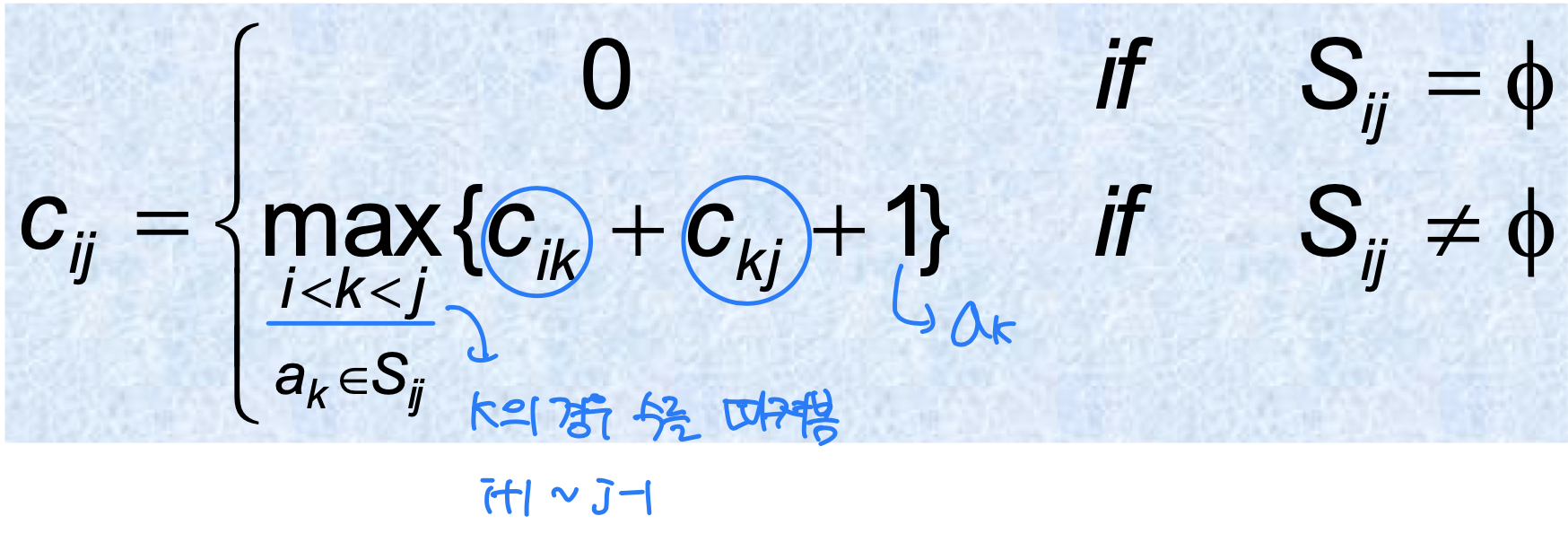
Theorem
a be the activity in S with the earliest finish time. Then,
1. a is used in some maximum-size subset of mutually compatible activities of S
2. S = , so that choosing a leaves S as the only nonempty subproblem.
Dynamic Programming vs. Greedy
- Number of subproblems
- Dynamic programming : Two subproblems are used in an optimal solution and there are
(j-1) – (i+1) + 1 = j – i – 1 choices when solving the subproblem S
- Greedy : Only one subproblem is used in an optimal solution and when solving the subproblems S, we need consider only one choice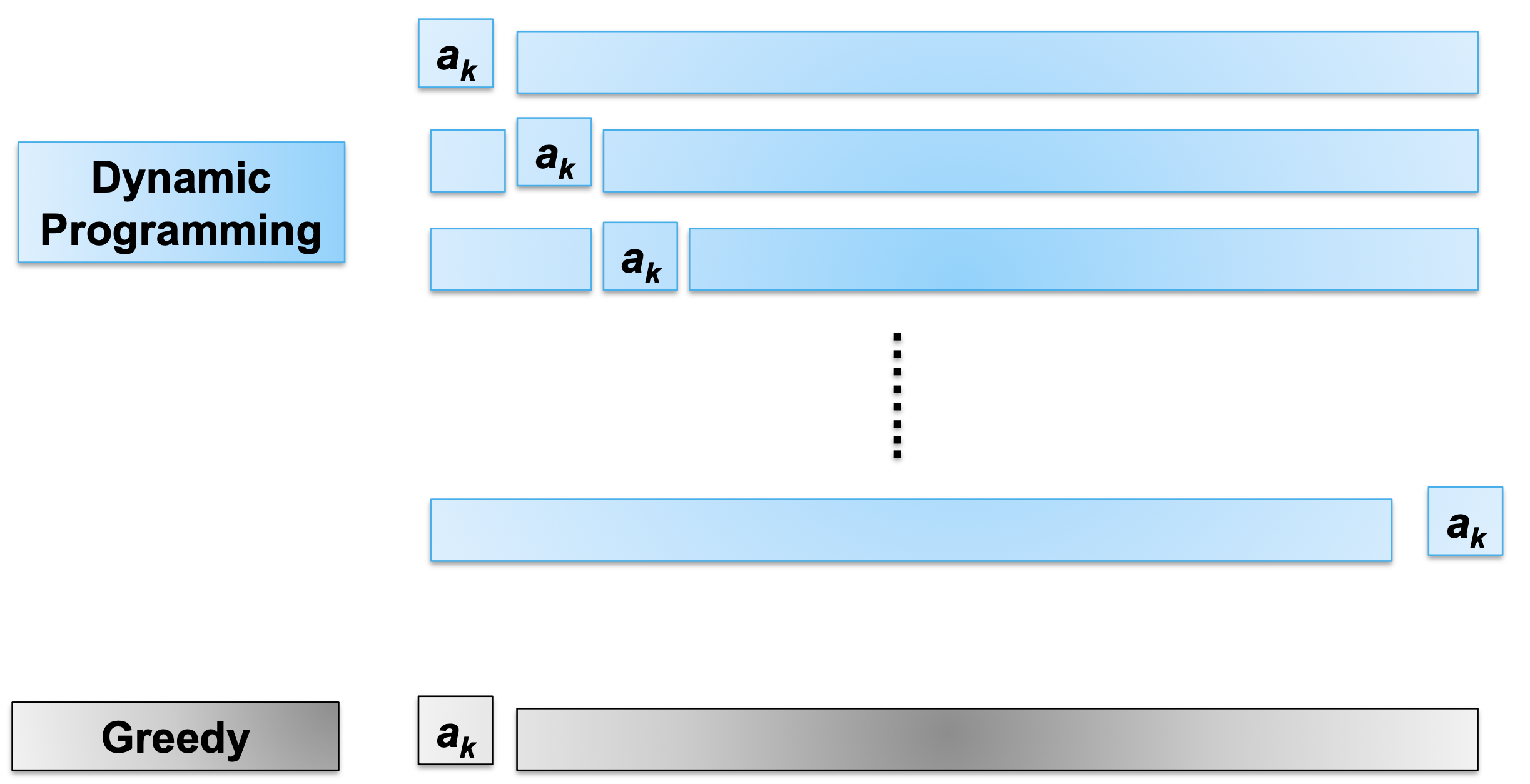
An activity-selection problem:greedy algorithm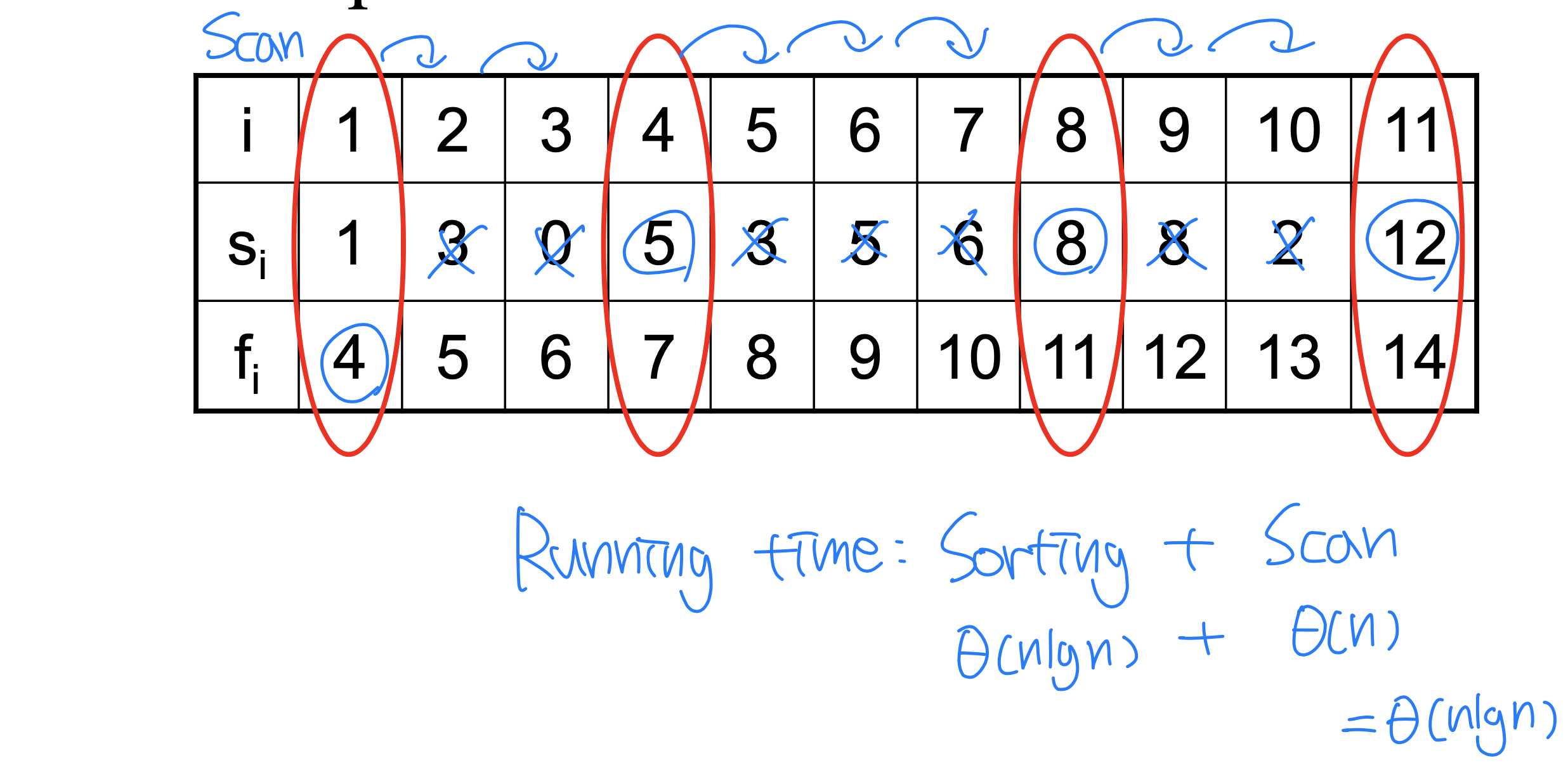
A Variation(변형) of the Problem
- Instead of maximizing the number of classes we want to schedule,
we want to maximize the total time the classroom is in use. - DP approach still remains unchanged.
- But greedy choices can't solve :
– Choose the class that starts earliest/latest
- Choose the class that finishes earliest/latest
- Choose the longest class
➡️ 어떤걸 하더라도 풀 수 x
⭐️ Greedy choice property
– An optimal solution can be obtained by making choices that seem best at the time, without considering their implications for solutions to subproblems.
Huffman Codes : Text Encoding
- Widely used
- Very effective technique for compressing data
- An optimal prefix code
- Goal: develop a code that represents a given text as compactly(간결하게) as possible
- A standard encoding is ASCII, which represents every character using 7 bits:
 ➡️ Require 133bits = 17bytes
➡️ Require 133bits = 17bytes - Of course, this is wasteful because we can encode 12 characters in 4( = 16 > 12) bits:
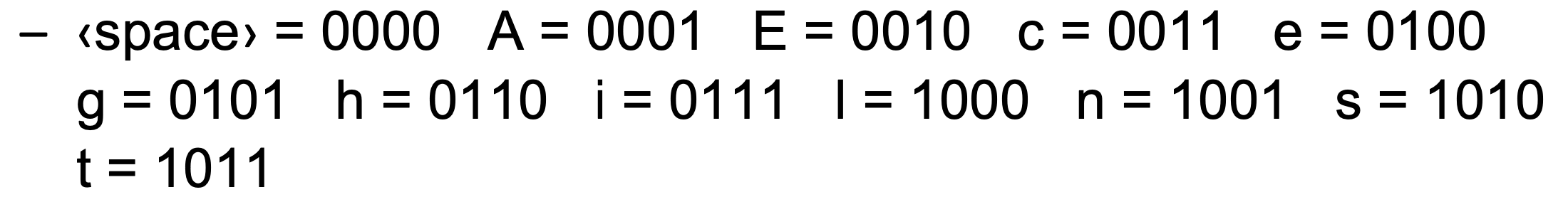 ➡️ Require 76bits = 10bytes
➡️ Require 76bits = 10bytes - An even better code(variable length) is given by the following encoding:
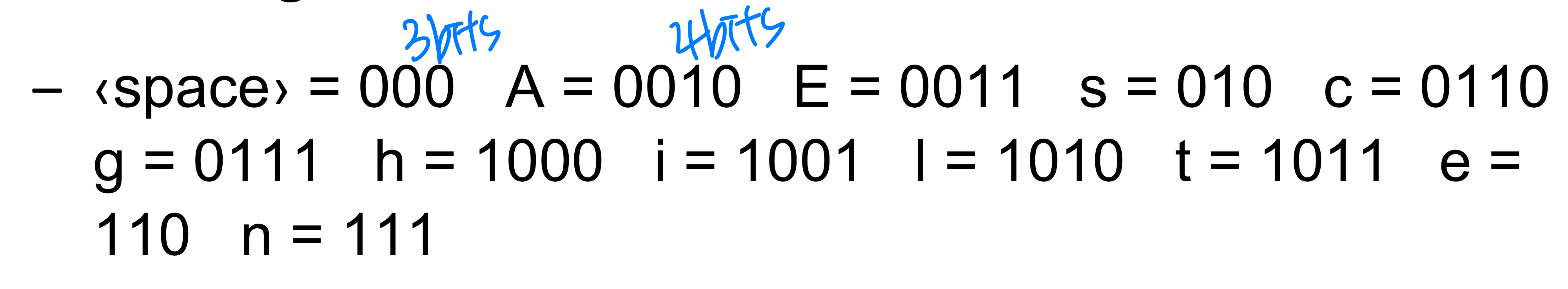 ➡️ Require 65bits = 9bytes
➡️ Require 65bits = 9bytes
Prefix code
- No codeword is a prefix of some other codeword
prefix: Ex_10110, 1011 is 4th prefix - The optimal data compression by a prefix code
- Easy to decode
- Non-prefix codes are ambiguous(모호한, 2가지 이상 해석가능한)
- If code is ambiguous, then it is not prefix code. Thus, if it is prefix code, it is unambiguous
Decoding / encoding tree : Fixed-length code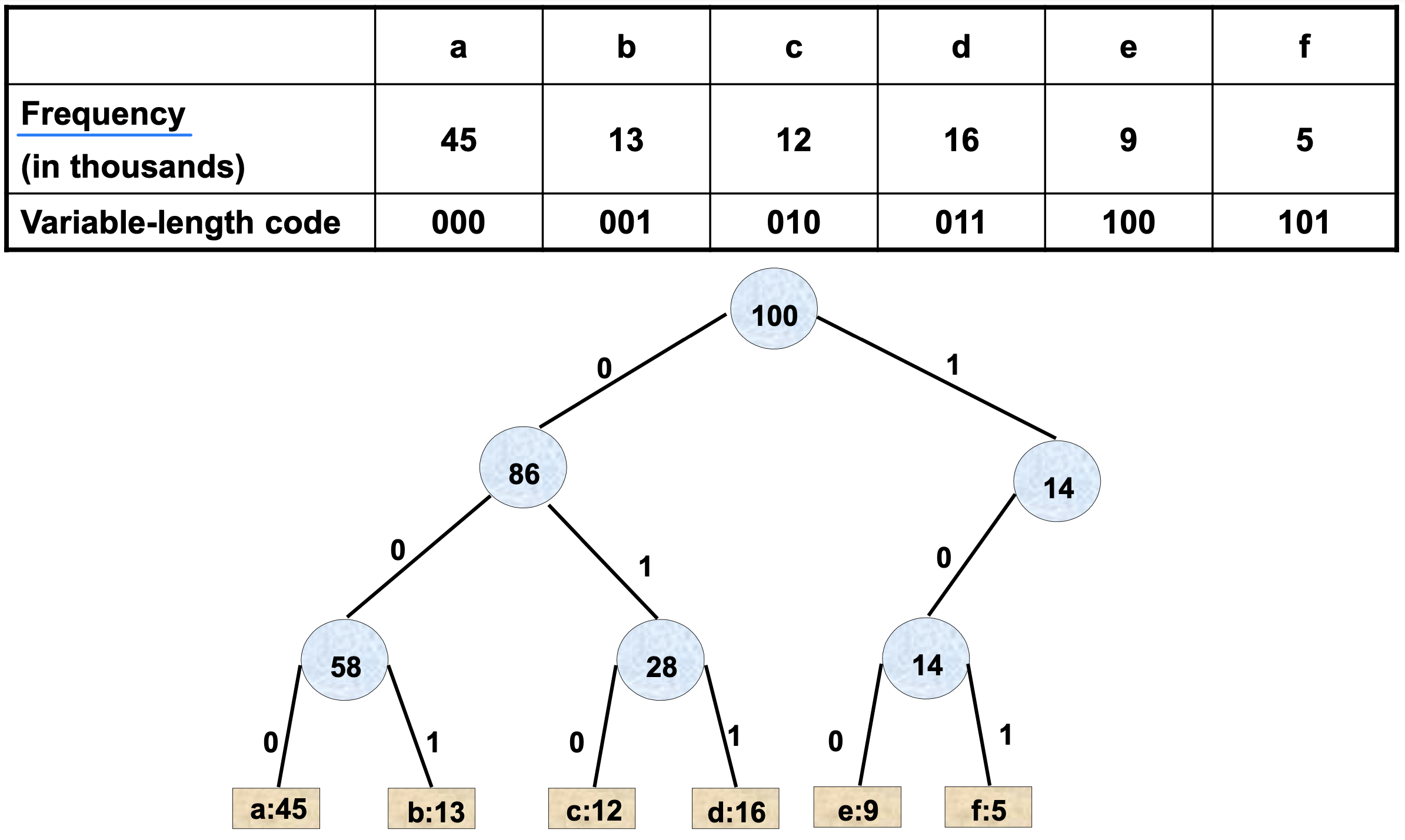
Decoding / encoding tree : Variable-length code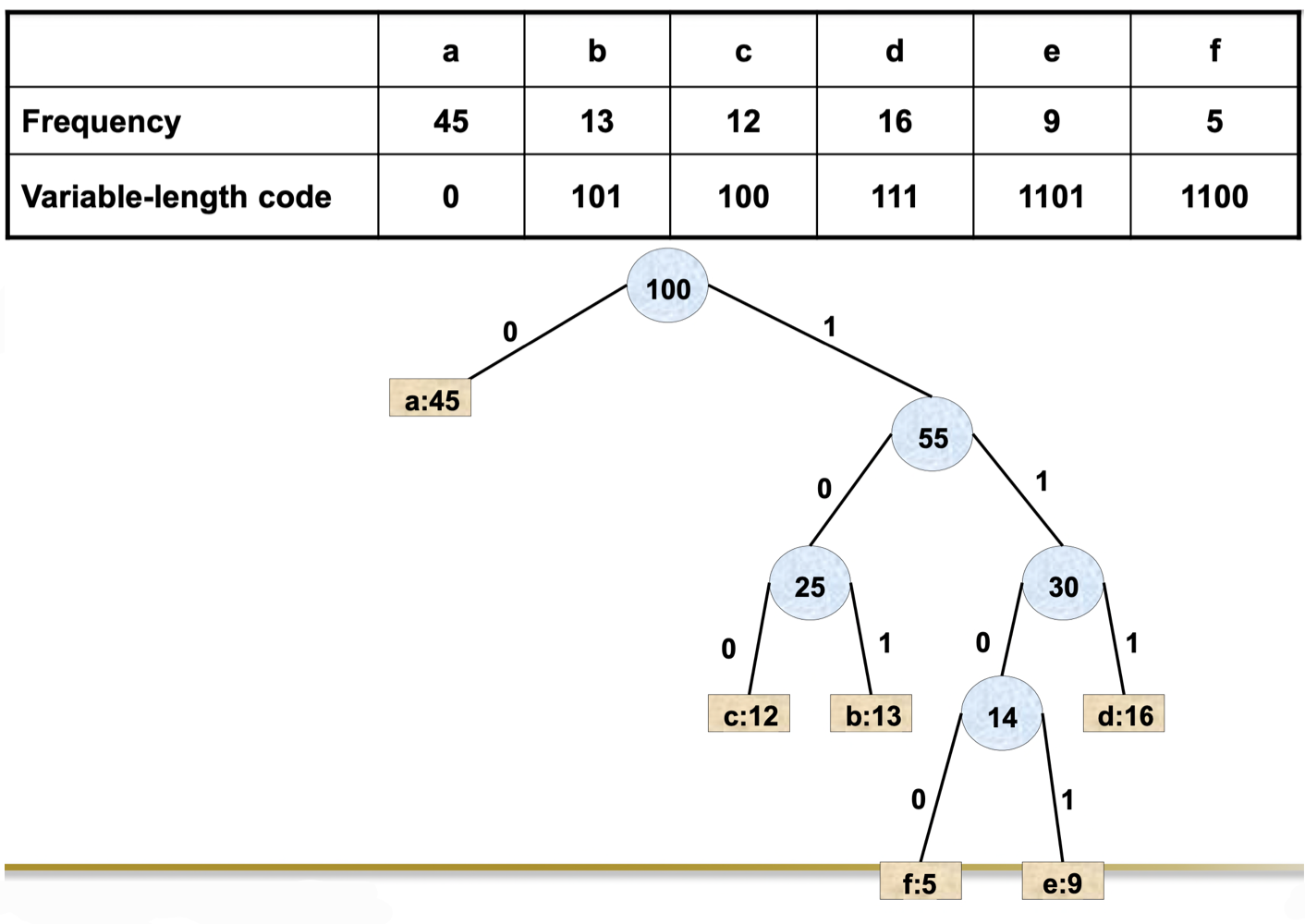
Cost of encoding a file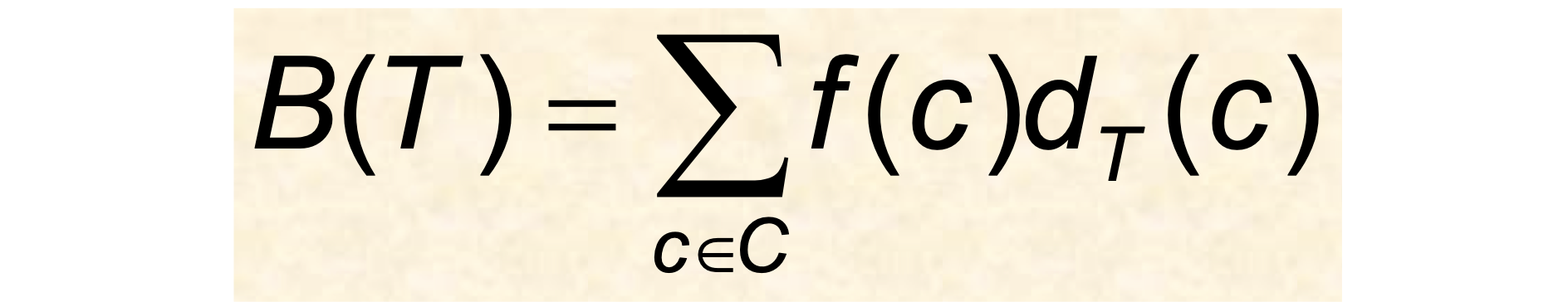
- T: tree corresponding to the coding scheme c in the alphabet C
- f(c): the frequency of c in the file
- d(c): the depth of c’s leaf in the tree
- B(T): the number of bits required to encode a file
Huffman's Algorithm
Huffman-Code(C) {
n = len(C) // cn
Q = C // O(lg n)
for i = 1 to n-1 // cn
do allocate a new node z
left[z] = Extract-Min(Q) // O(lg n)
right[z] = Extract-Min(Q) // O(lg n)
f[z] = f[left[z]] + f[right[z]] // c
Insert(Q, z) // O(lg n)
return Extract-Min(Q)
}➡️ Running time: O(n lg n) : lg n을 n번 반복
- Ex_
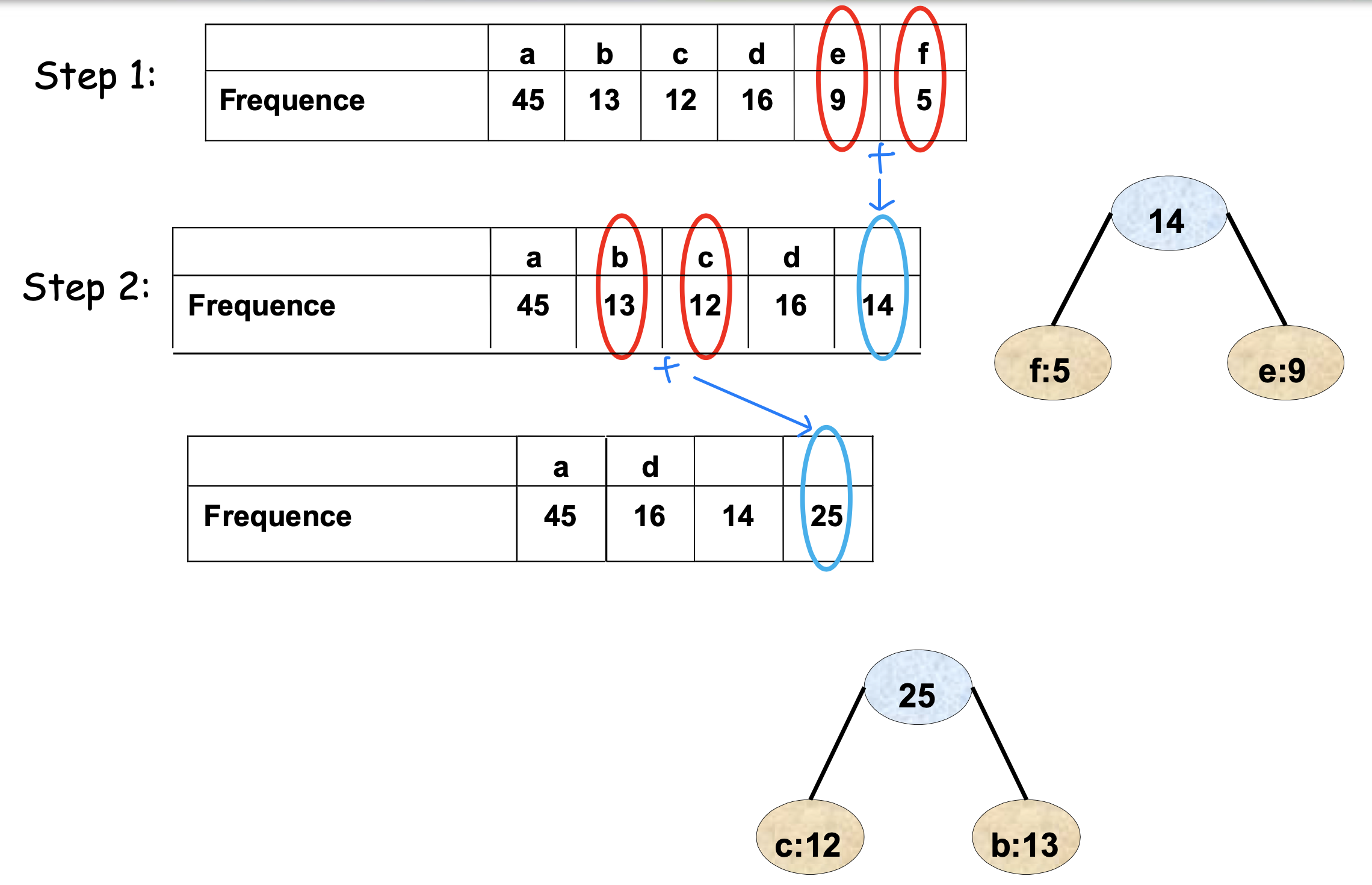
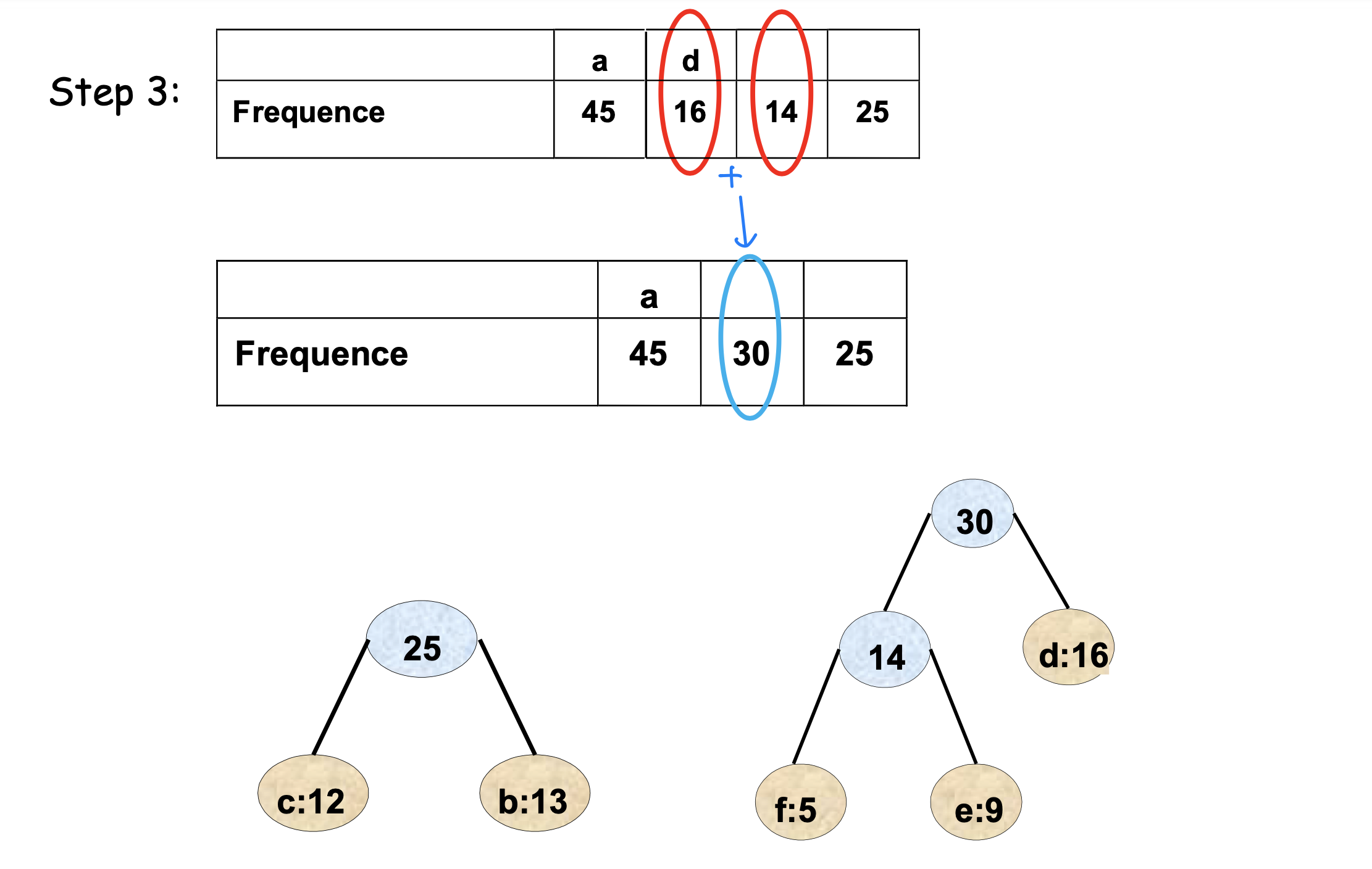
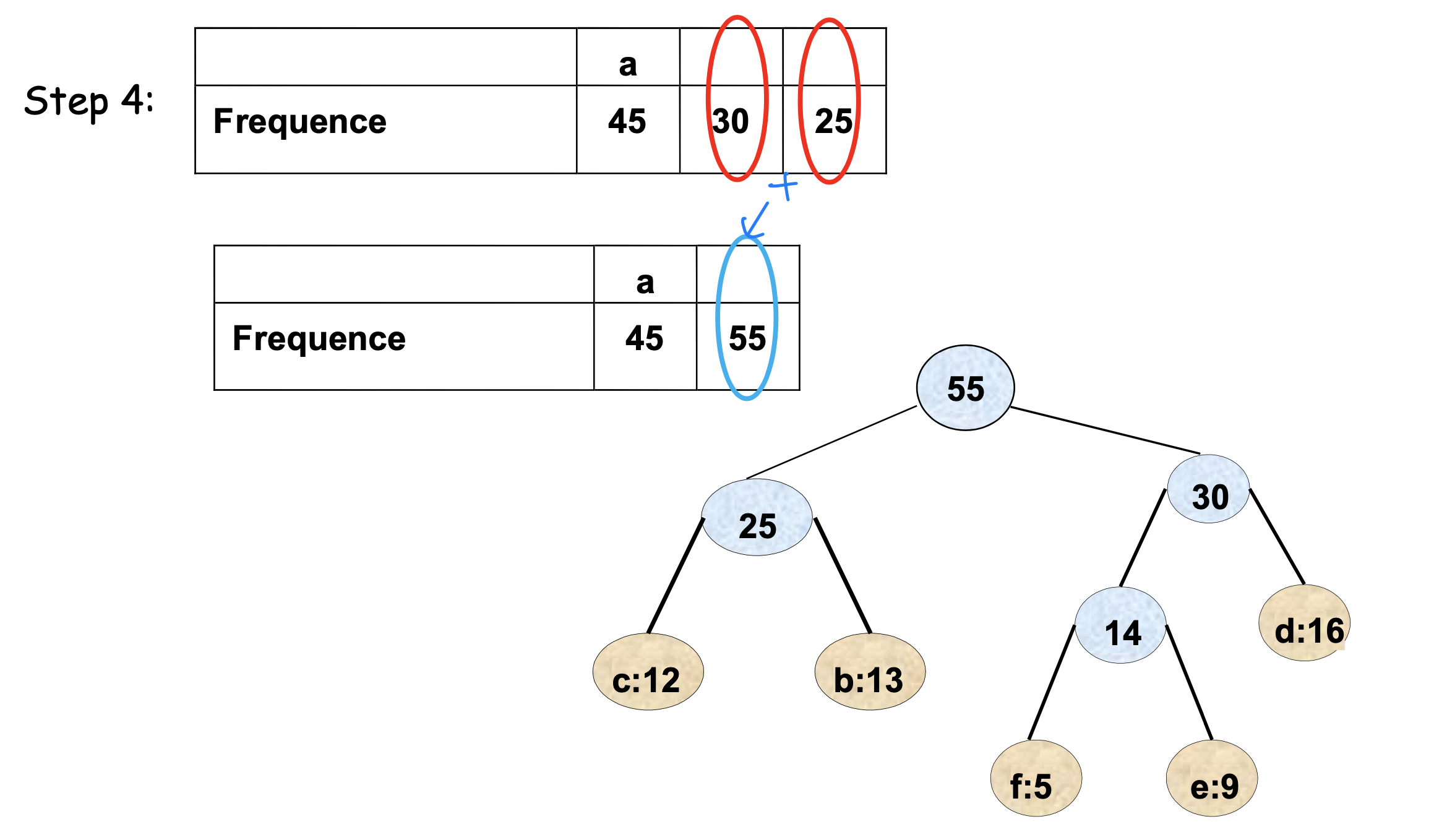
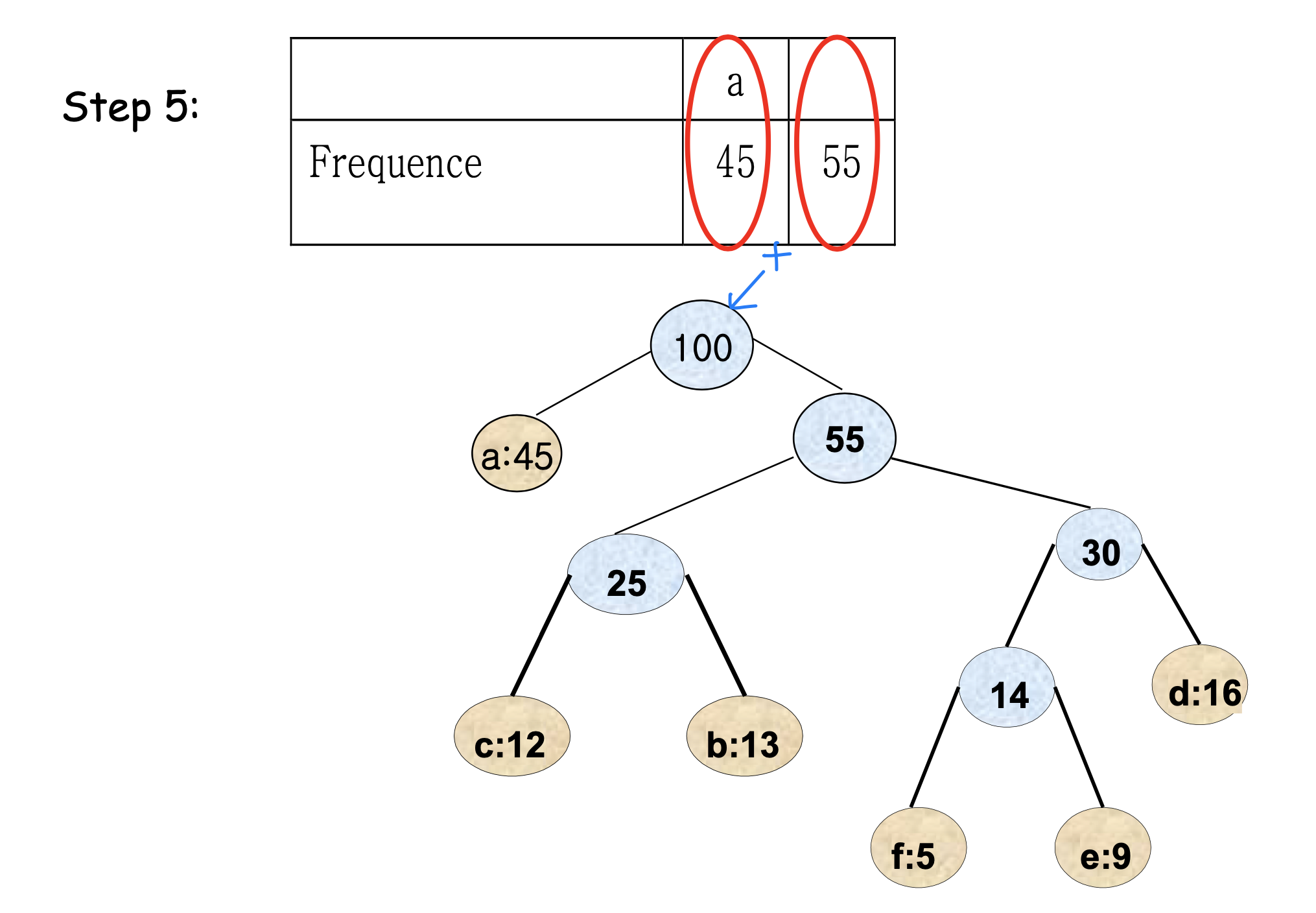
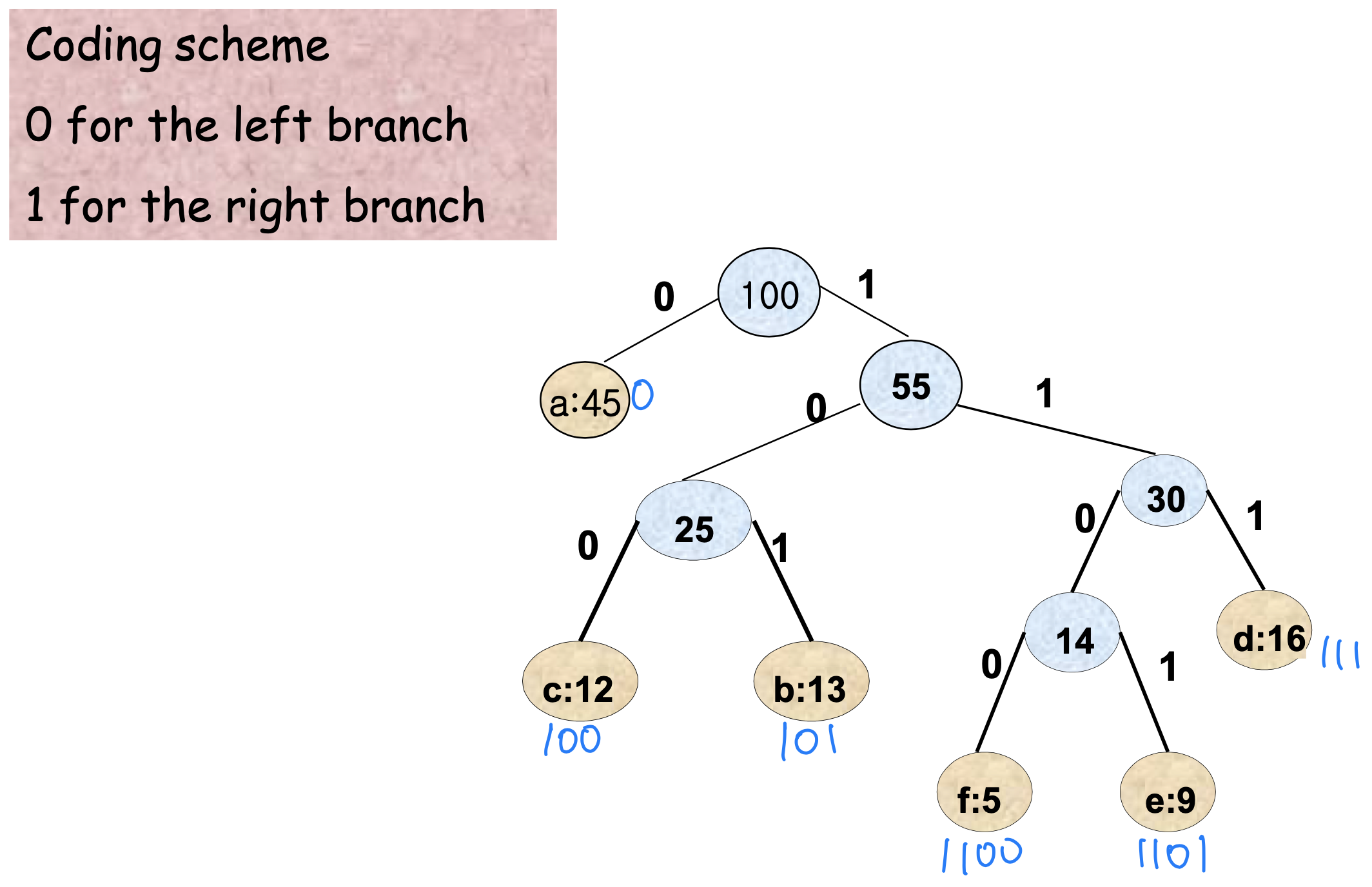 ➡️ Coding scheme 잘보기!
➡️ Coding scheme 잘보기!
Exercise in class
1. Coin exchange by greedy, counter example
➡️ Denomanation of coins = { 1, 10, 25 }, change = 30
2. Coin exchange by DP
Recurrsive equation
V : change
num[V] :min number of coins for change V
coins[1...m] : denomanation of each coin from to m ➡️ O(nm)
➡️ O(nm)
3. Activity selection problem
Show counter example
The greedy approach of selecting the activity of least duration from among those that are compatible with previously selected activities.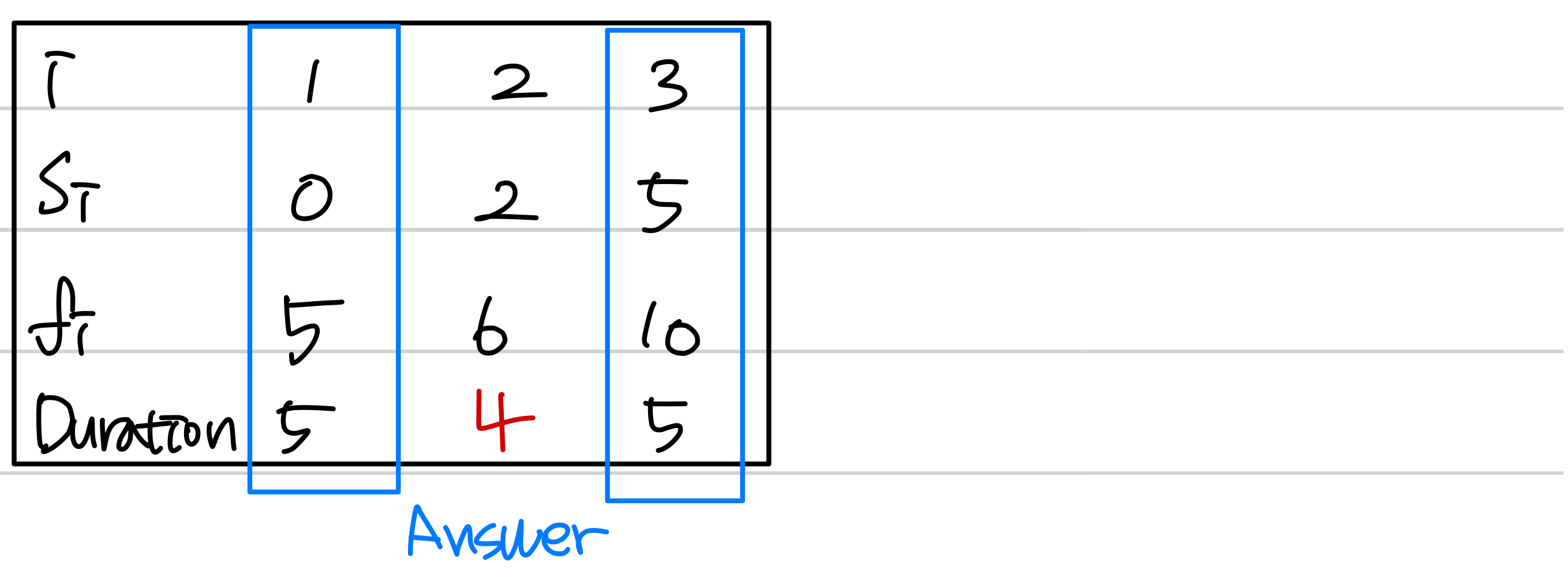 ➡️ will pick a, but the solution is a, a
➡️ will pick a, but the solution is a, a
4. Huffman
| a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
Left branch : 0
Right branch : 1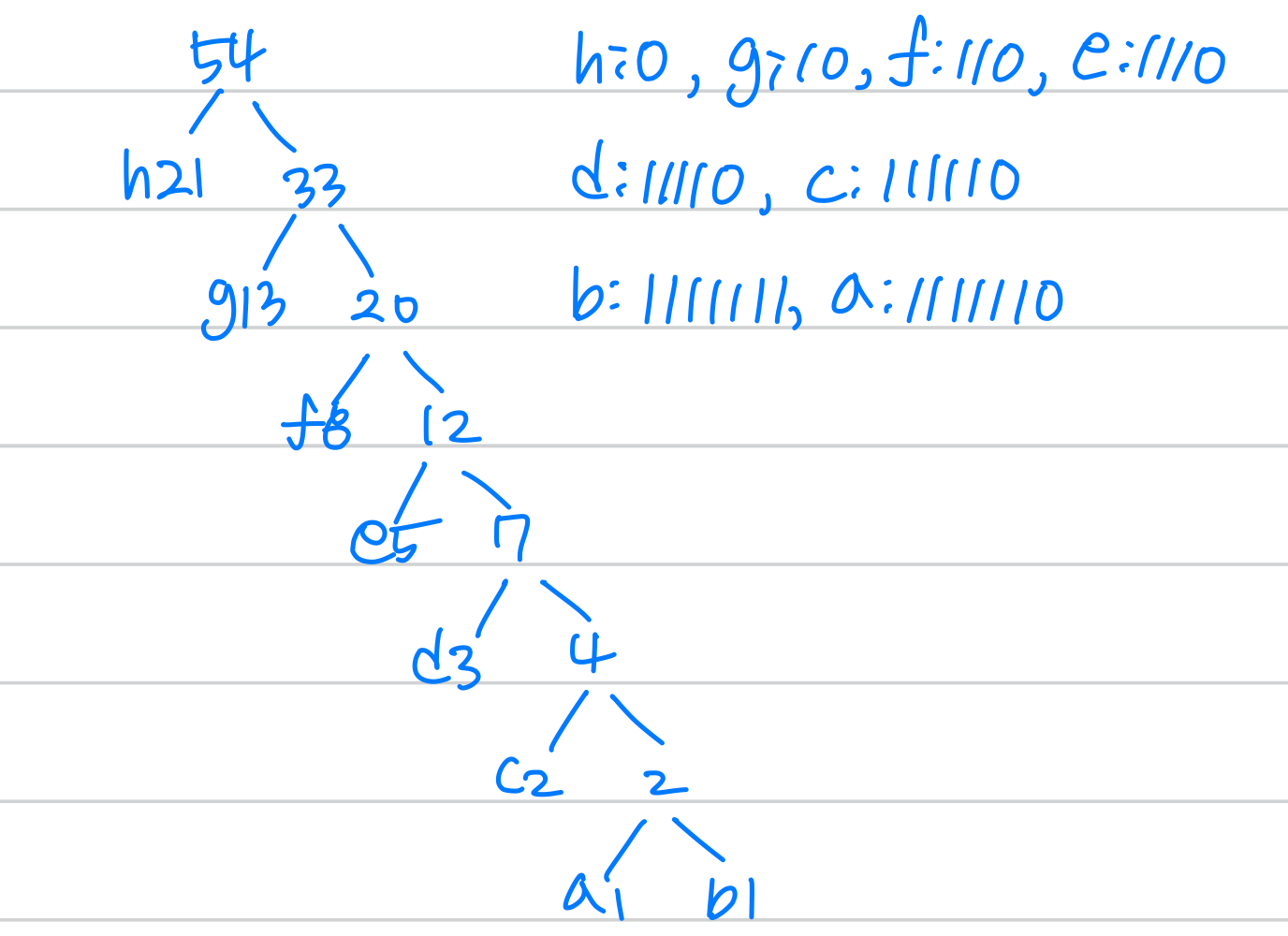 ➕ After 'c' is extracted from queue, What is the frequency of new node??
➕ After 'c' is extracted from queue, What is the frequency of new node??
➡️ 2
5. Greedy로 풀려면 꼭 증명?
➡️ Yes, Greedy choice property
HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.

