
🖥️ MST
Spanning Tree : Spanning graph + Tree(acycle)
- Problem: given a connected, undirected, weighted graph, find a spanning tree using edges that minimize the total weight
- Undirected graph G = (V, E)
- Weight w(u,v) on each edge (u,v) E
- Spanning tree of G’ is a minimal subgraph of G such that
- V(G’) = V(G) and G’ is connected
- Any connected graph with n vertices must have at least n-1 edges. All connected graphs with n-1 edges are trees.
➡️ connected + n vertices + n-1 edges : cycle이 없음을 의미
- Find T E s.t.
- T connects all vertices (T is a spanning tree), and
- w(T) = w(u,v)(모든 edge weight의 합) is minimized
- Has n -1 edges, no cycle, might not be unique
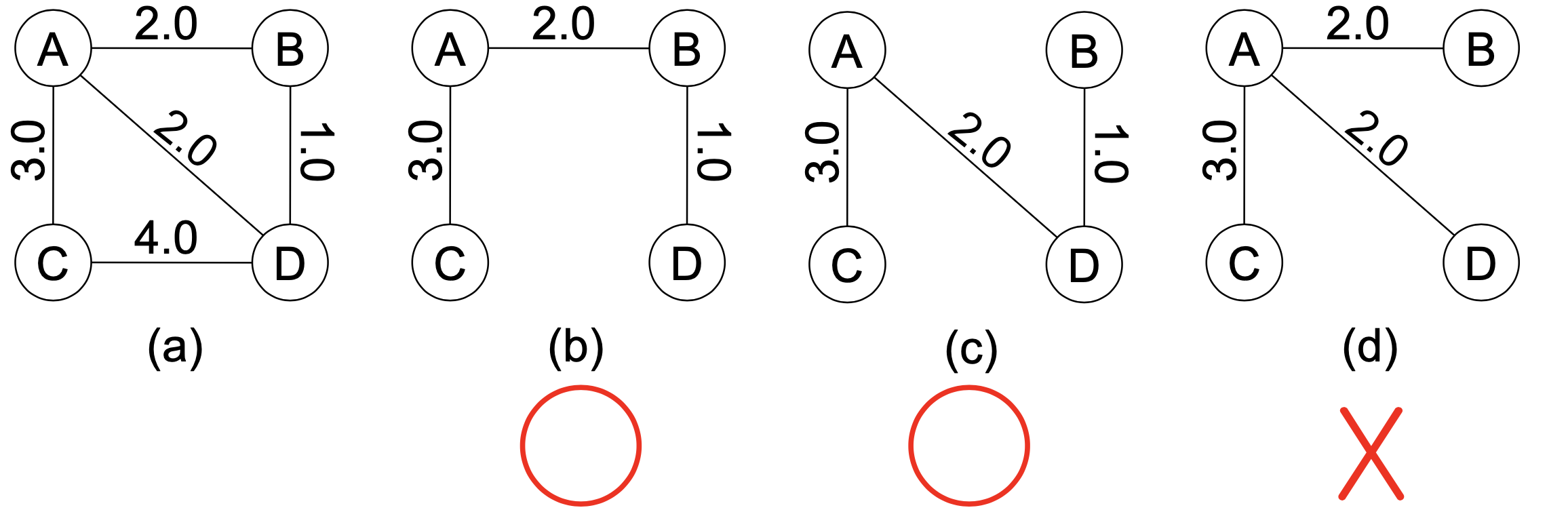
- Example)
Interconnect n pins with n-1 wires, each connecting two pins so that we use the least amount of wire. - We’ll look at two greedy algorithms
- Kruskal’s algorithm
- Prim’s algorithm
Building up the solution
- Build a set A of edges
- Initially, A is empty
- As we add edges to A(= n-1, exit), maintain a loop invariant : A is a subset of some MST
- Add only edges that maintain the invariant(불변성)
- If A is a subset of some MST, an edge (u,v) is safe for A if and only if A U { (u,v) } is also a subset of some MST
- So, we will add only safe edges
Generic MST algorithm ➡️ safe : looks best (smallest or largest)
➡️ safe : looks best (smallest or largest)
Finding a safe edge
- Let S V and A E
- A cut (S, V – S) is a partition of vertices into disjoint sets S and V – S
- Edge (u, v) E crosses cut (S, V – S ) if one endpoint is in S and the other is in V – S
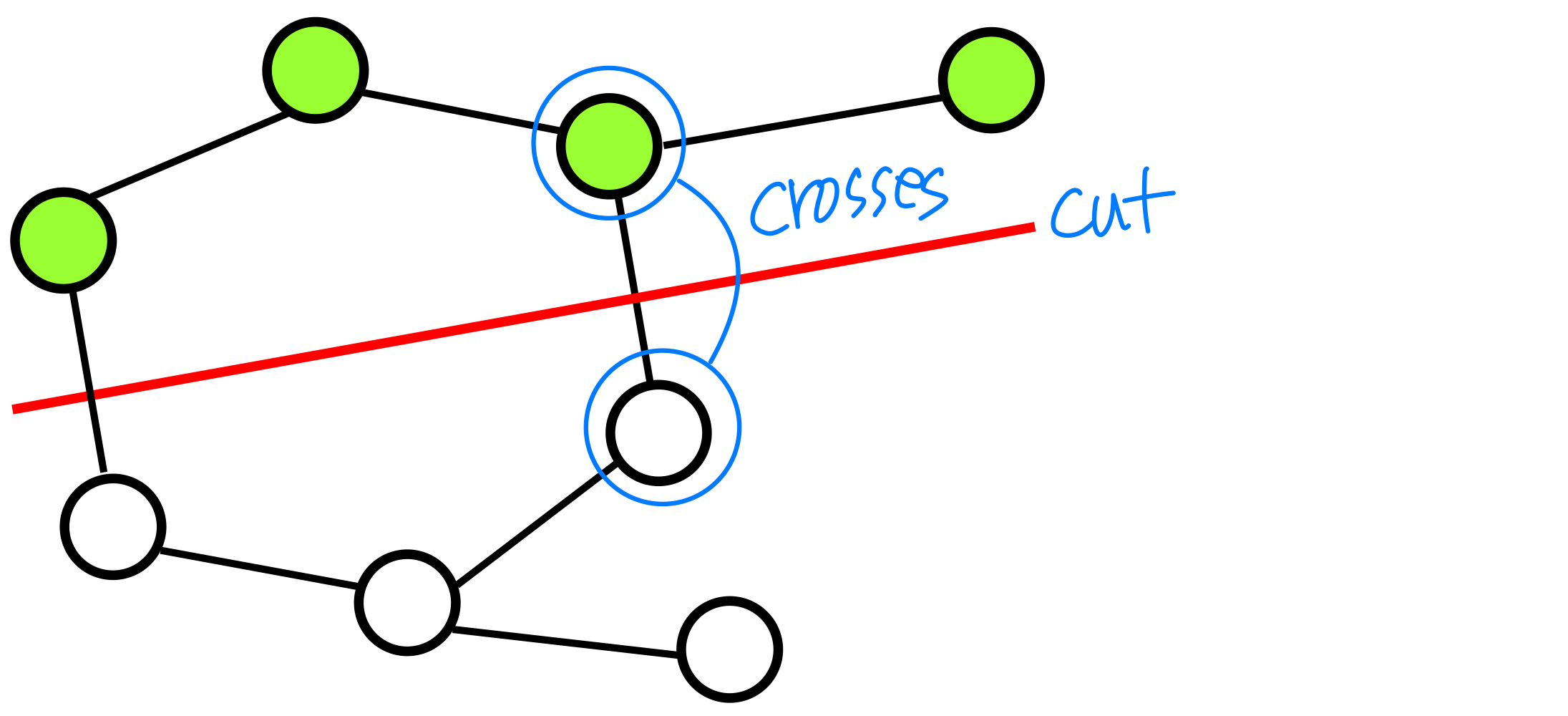
- A cut respects A if and only if no edge in A crosses the cut
➡️ cut을 지나가지 않음 - An edge is a light edge crossing a cut if and only if its weight is minimum over all edges crossing the cut. For a given cut, there can be more than one light edge crossing it (값이 같으면 여러개)
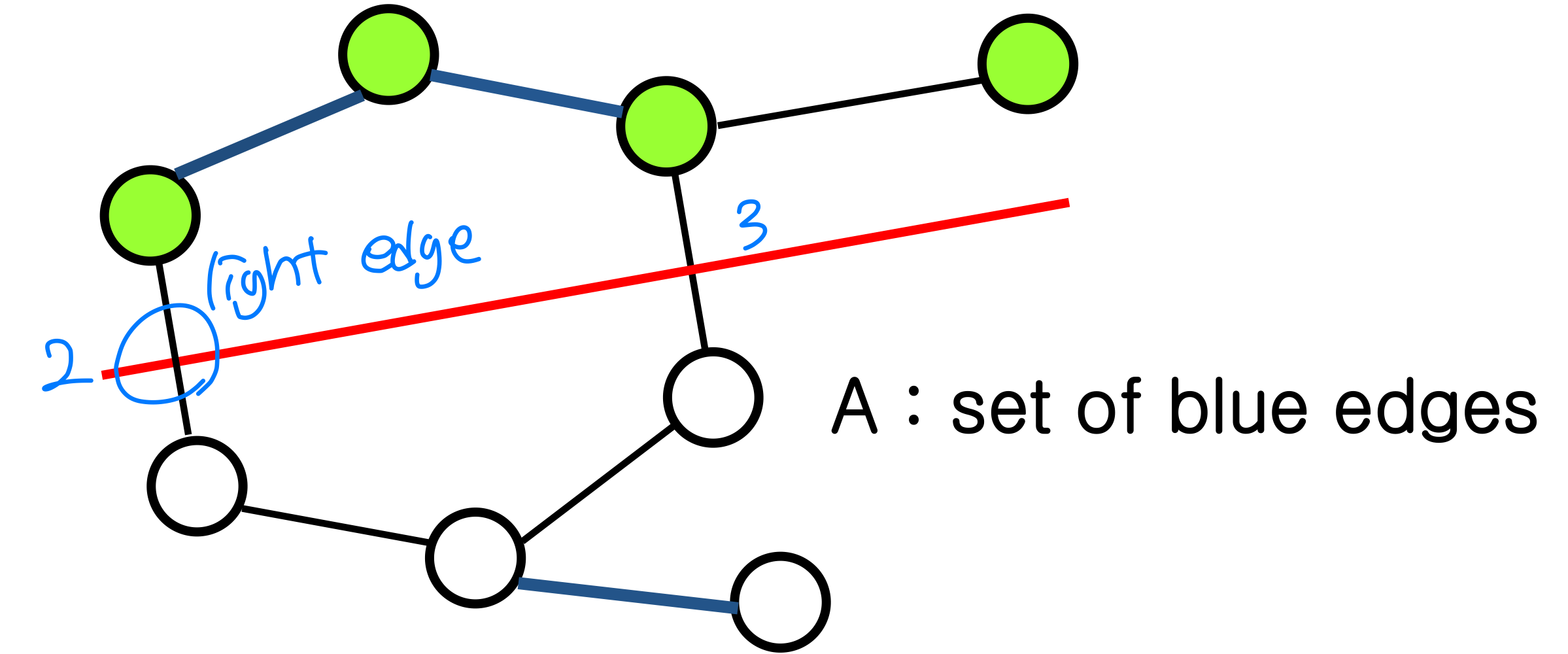
Theorem
Let A be a subset of E in some MST, (S, V – S) be a cut that respects A, and (u, v) be a light edge crossing (S, V – S )
Then, (u, v) is safe for A
Proof)
1. Let T be a MST that includes A, and assume that T does not contain the light edge (u, v)
2. We shall construct another MST T ́ that includes A U { (u,v) } .
3. Edge (u,v) forms a cycle with the edges on the path p from u to v in T
➡️ n -1 edge에서 n개가 되기 떄문
4. Since u and v are on opposite sides of the cut (S, V – S) there is at least one edge in T on the path p that also crosses the cut. Let (x,y) be any such edge.
5. Removing (x,y) breaks T into two components. And adding (u,v) reconnects them to form a new spanning tree T ́
w(T ́) = w(T) – w(x,y) + w(u,v) ≤ w(T)
Thus, T ́ must be a MST
And since A U { (u,v) } T ́, (u,v) is safe for A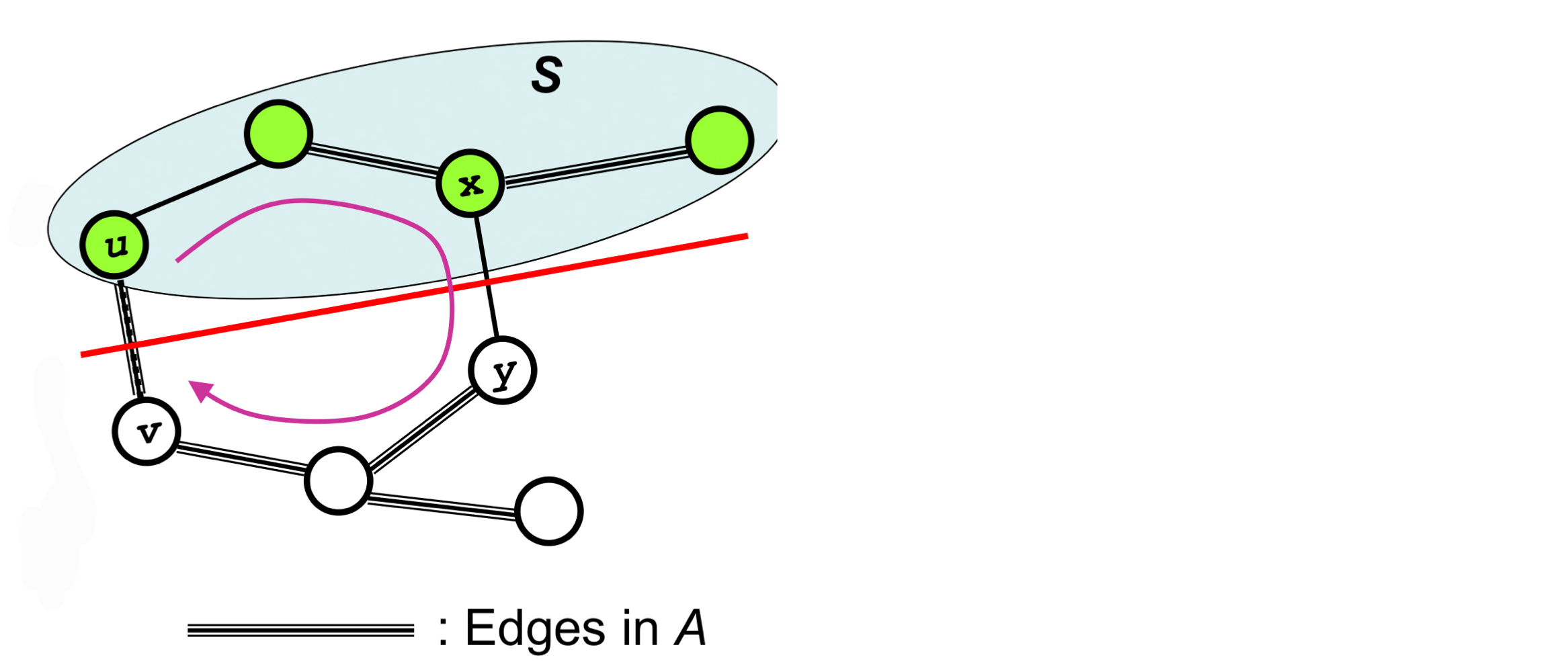
Corollary
Let A be a subset of E that is included in some minimum spanning tree for G, and let C = (V, E) be a connected component (tree) in the forest G = (V, A). If (u,v) is a light edge connecting C to some other component in G, then (u,v) is safe for A
Proof) The cut (Vc, V – Vc) respects A, and (u,v) is a light edge for this cut. Therefore, (u,v) is safe for A.
🖥️ Kruskal’s algorithm
- Sort edges into nondecreasing(increasing) order by w.
- The algorithm maintains A, a forest of trees ➡️ 마지막에 big one tree
- Repeatedly merges two components into one by choosing the light edge that connects them
i.e.,
1. Choose the light edge crossing the cut between them.
2. (If it forms a cycle, the edge is discarded) - What is the design strategy of Kruskal’s algorithm?
- Greedy
pseudo-code
Example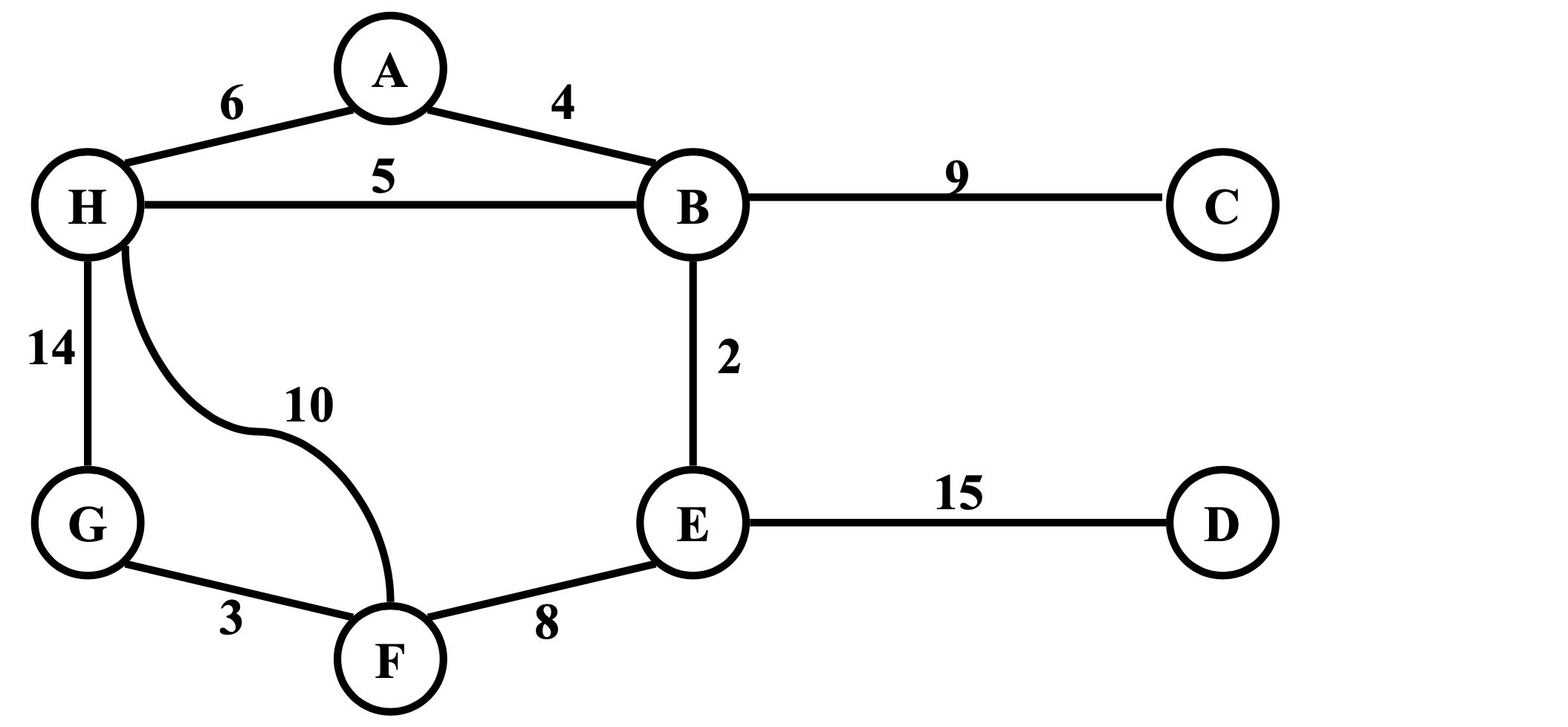
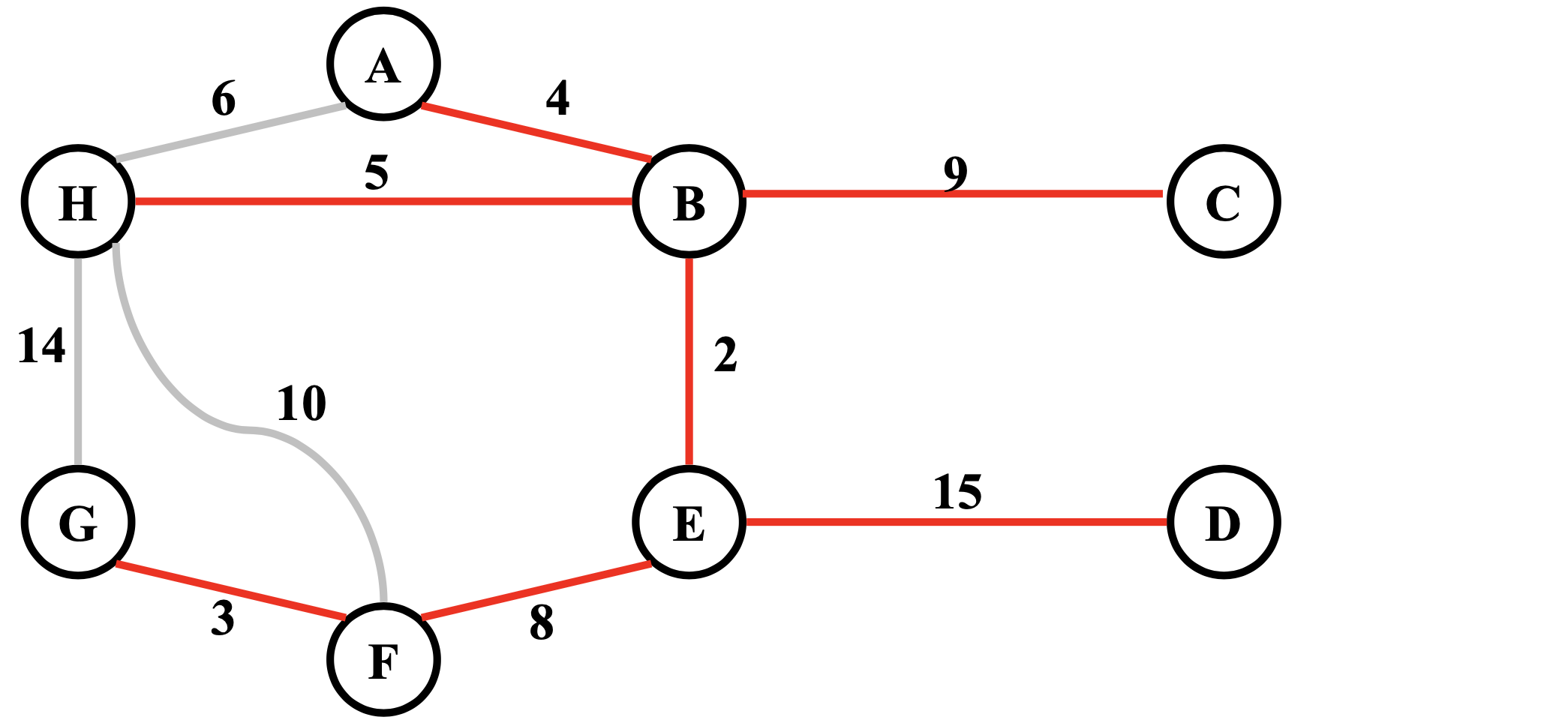
🖥️ Prim's algorithm
- Builds one tree, so A is always a tree (cf. kruskal is forest)
- Start from an arbitrary “root” r
- At each step, find a light edge crossing cut (V, V – V), where V = vertices that A is incident on
- [v] = parent of v, NIL if it has no parent or v = r.
- To find a light edge quickly
- use a priority queue Q
Outline
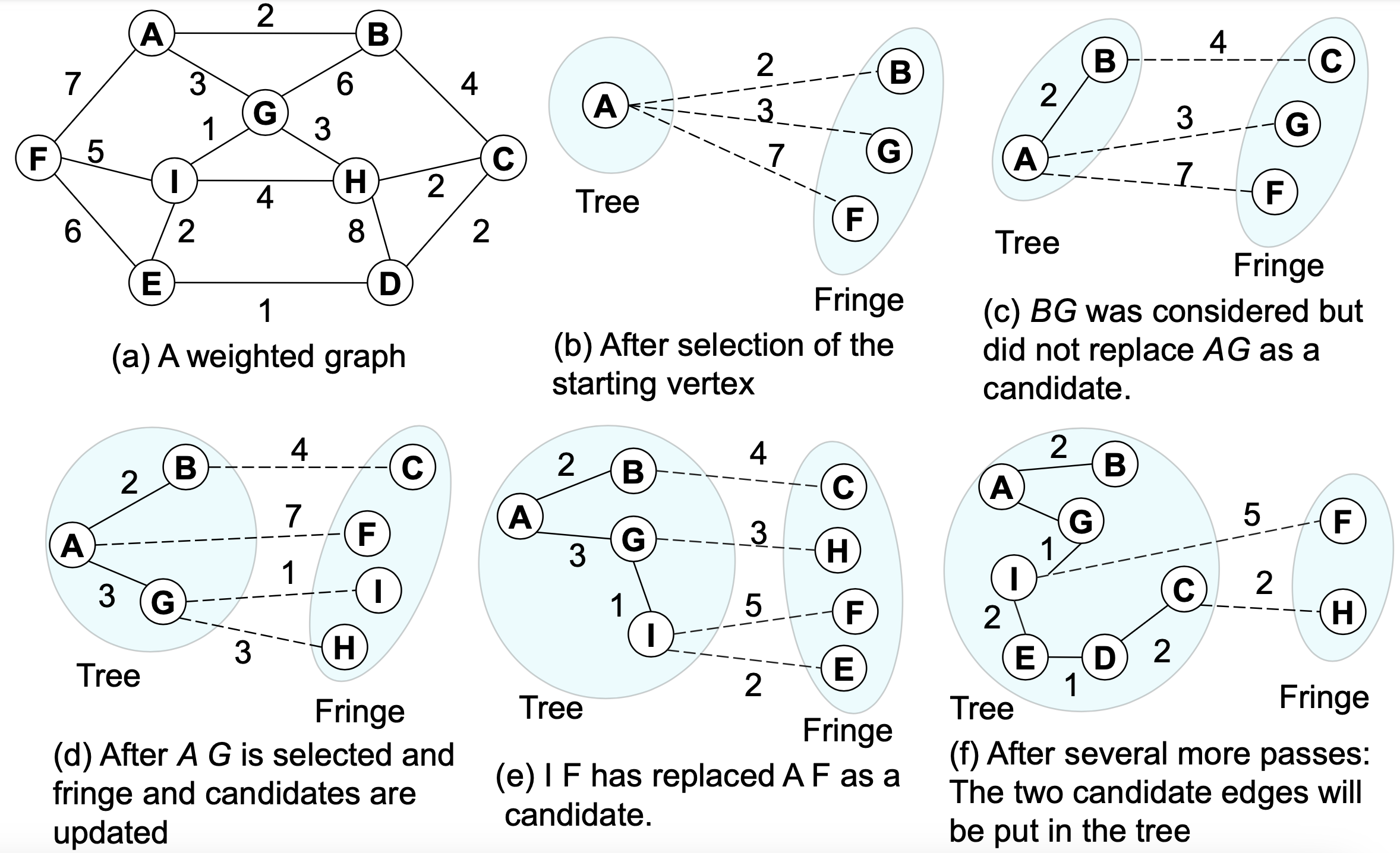
pseudo code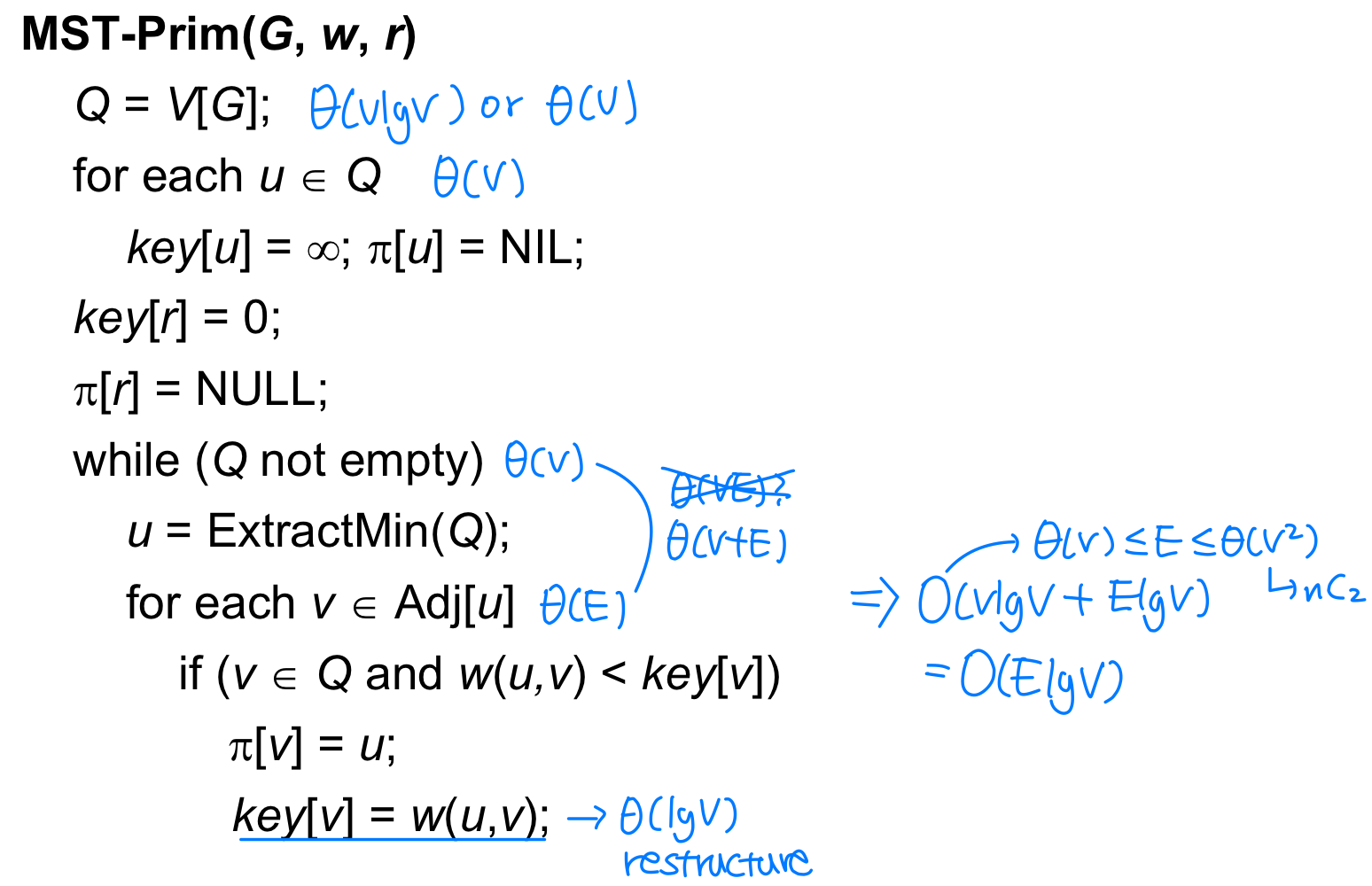
Exercise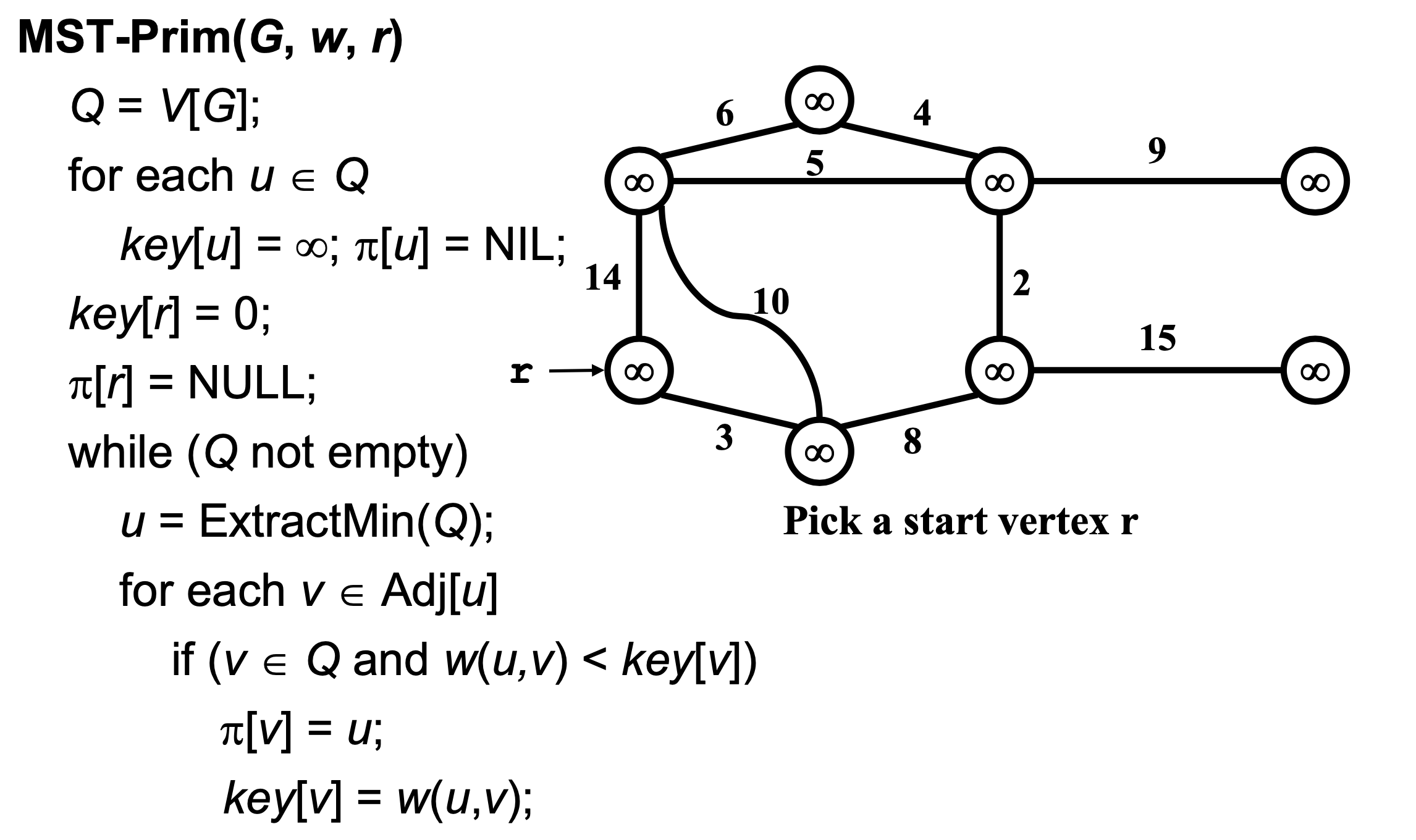
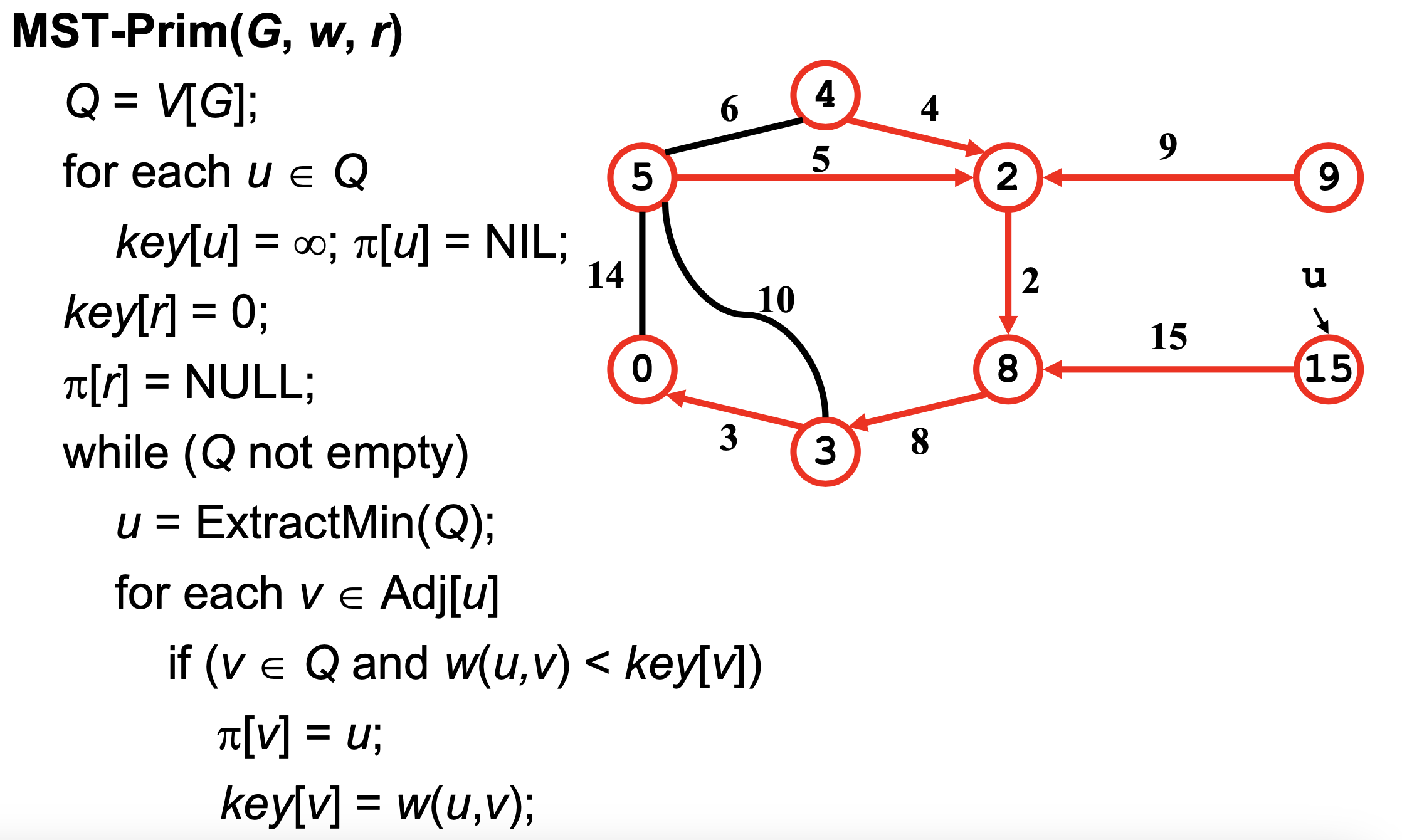
—
🖥️ Exercise in class
Data structure used for Prim's algorithm
A .Priority Queue ➡️ Greedy 유추가능
Greedy는 PQ만 사용? ➡️ No, sorted arr vs. PQ. : key값이 바뀌면 array는 다시 sort(nlgn), but PQ는 lgn
HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.
