[ Algorithm ] 09. Shortest Paths

• Input : directed graph G = (V, E) with weight function w : E → R
• Determine the path p with minimum weight from source to destination
• Weight w(p) of path p : sum of edge weights on path p
• shortest-path weight u to v :
• Variants
  • Single-source shortest path : find shortest paths from a given source vertex s $\in$ V to every vertex v $\in$ V
  • Single-destinations : find shortest paths to a given destination vertex. By reversing the direction of the each edge in the graph, the problem is reduced to single-source problem
  • Single-pair : find shortest path from u to v. No easier(더 빠르게 X) than single-source problem
  • All-pairs shortest-paths : find shortest path from u to v for all u, v $\in$ V
    
    
• Single-source shortest path
  • Bellman-Ford algorithm
  • In DAG
  • Dijkstra’s algorithm
• All-pairs shortest-paths
  • Floyd-Warshall algorithm

Shortest Path Properties

Lemma 24.1
Again, we have optimal substructure: the shortest path consists of shortest subpaths:
➡️ Proof: suppose some subpath is not a shortest path
- There must then exist a shorter subpath
- We could substitute the shorter subpath for a shortest path
- But then overall path is not shortest path. Contradiction

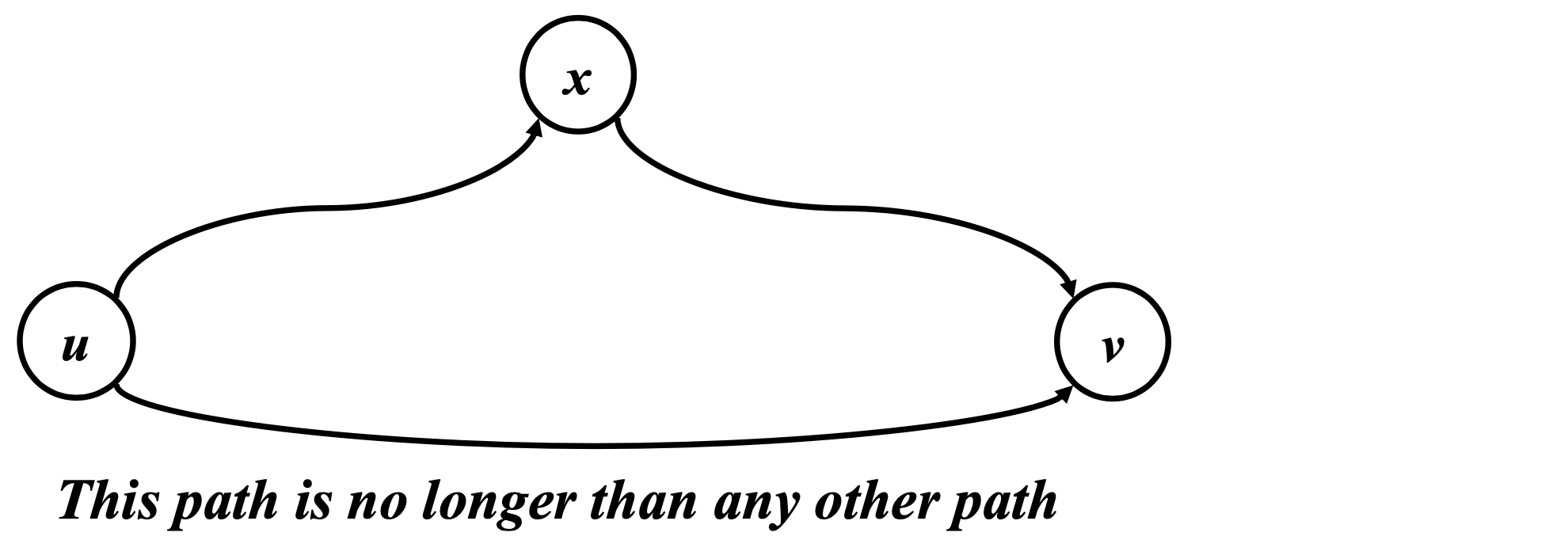
• Define δ(u,v) to be the weight of the shortest path from u to v. Shortest paths satisfy the triangle inequality: δ(u, v) $\le$ δ(u, x) + δ(x, v)

Negative-weight edges

• OK, as long as no negative-weight cycle are reachable from the source
• If we reach a negative-weight cycle, we can just keep going around it and get w(s, v) = -$\infin$ for all v in the cycle
• Some algorithms work only if there are no negative-weight edges

Cycles

• Shortest paths can’t contain cycles
  • We assumed that there is no negative-weight cycles
  • Positive-weight cycle : Just omit(생략) it to get a shorter path
  • Zero-weight cycle : There is no reason to use them. Assume that our solutions won’t use them.

🖥️ Single Source Shortest Path

• Find shortest paths from a given source vertex s $\in$ V to every vertex v $\in$ V
• Output for each vertex v $\in$ V :
  • d[v] = δ(s, v)
    • Initially, d[v] = $\infin$
    • Reduces d[v] as algorithm progress.
      But always maintain d[v] $\ge$ δ(s, v)
    • d[v] : shortest-path estimate(추정)
  • $\pi$[v] = predecessor(전임자) of v on a shorteat path from s.
    • If no predecessor, $\pi$[v] = NIL
    • $\pi$ induces a tree – shortest-path tree

Initialization

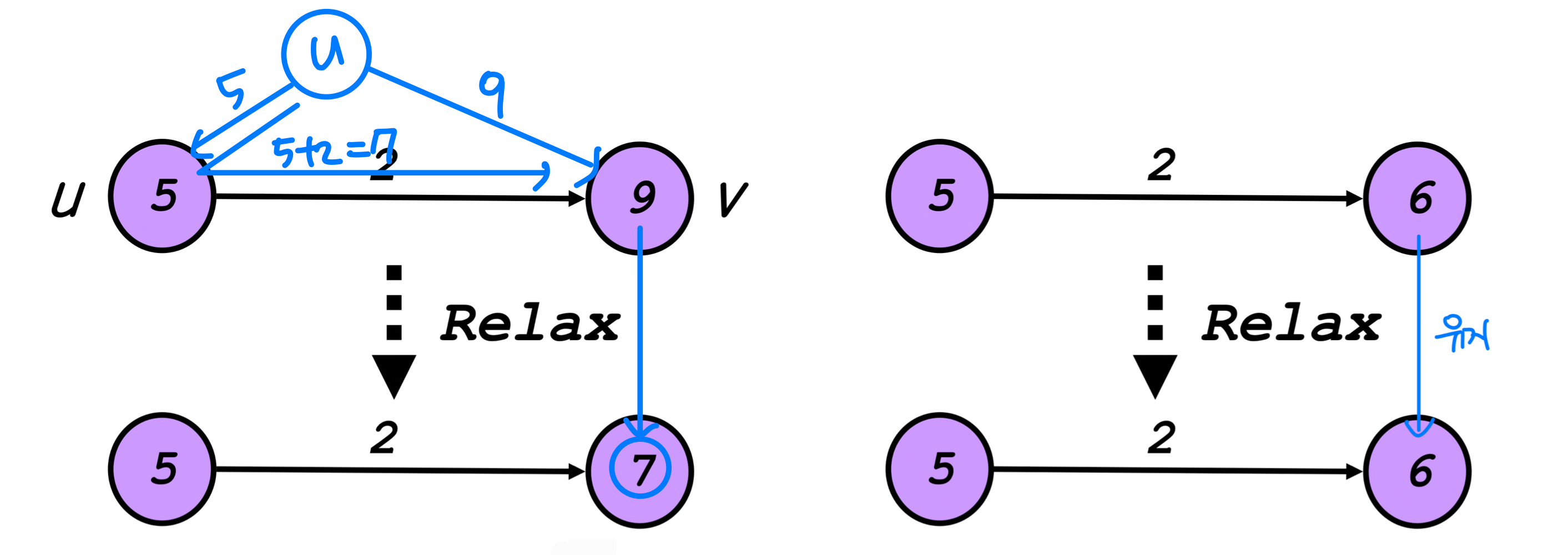
Relaxation

• A key technique in shortest path algorithms is relaxation
  • Idea: for all v, maintain upper bound d[v] on δ(s,v)!
• 

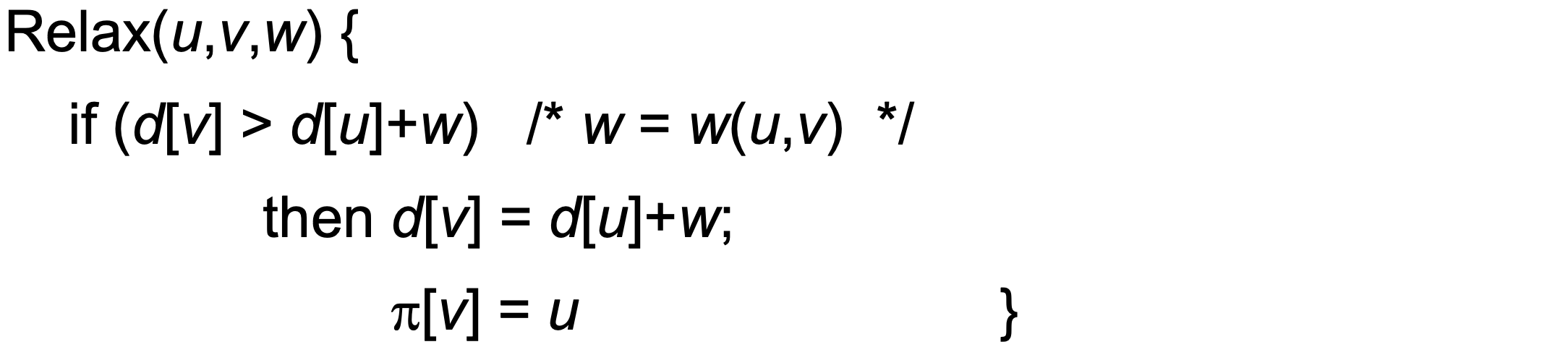
[1] Bellman-Ford algorithm

• Solves the single-source shortest-paths problem in general case in which edge weights may be negative
• Allow negative-weight edges and produce a correct answer as long as no negative-weight cycles are reachable from the source
• Returns a boolean value
  • negative-weight cycle – FALSE
  • No such cycle – TRUE

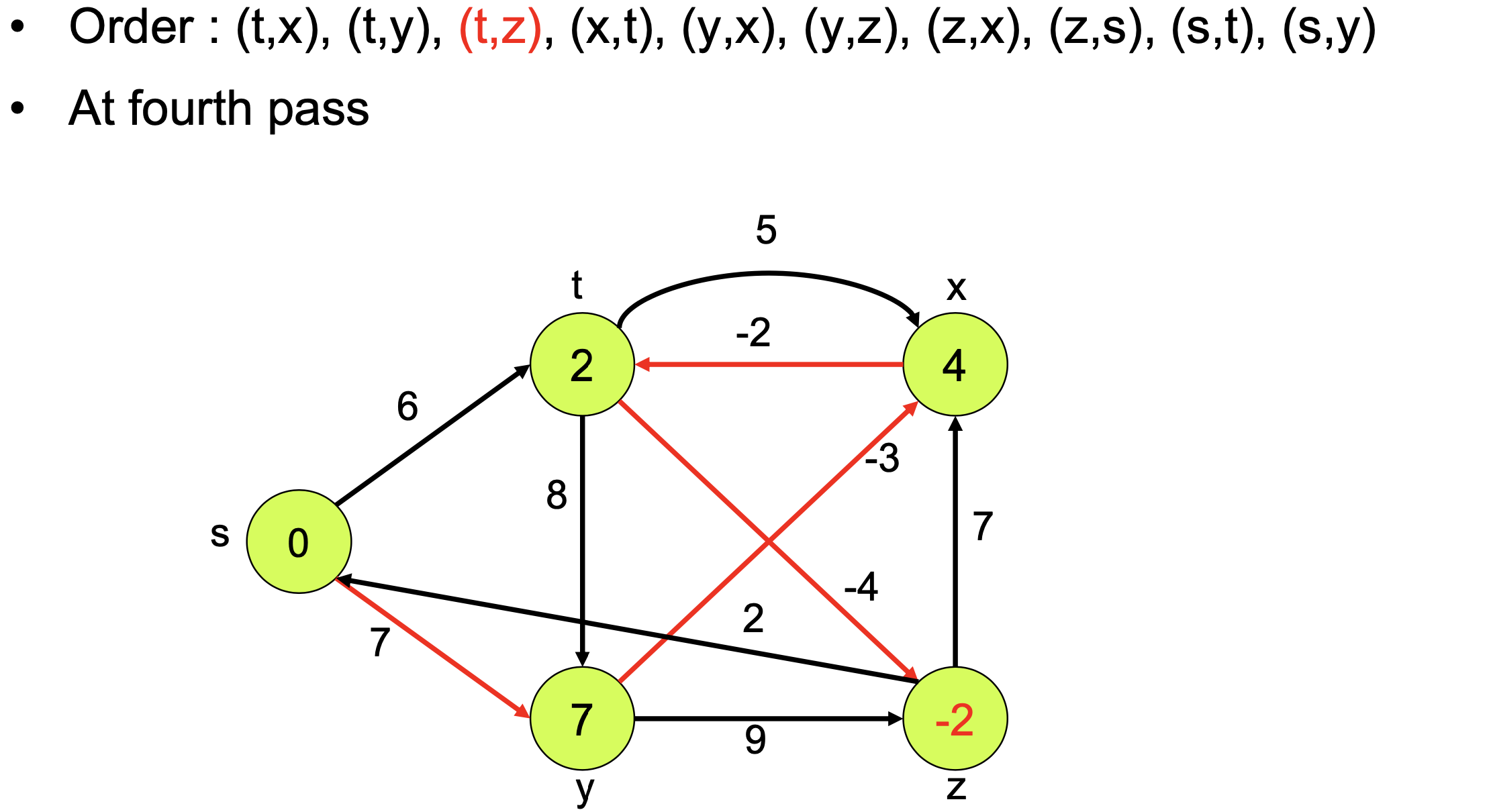
Pseudo-codeThe first loop relaxes all edges |V| - 1 times

Time : Θ(VE)

Example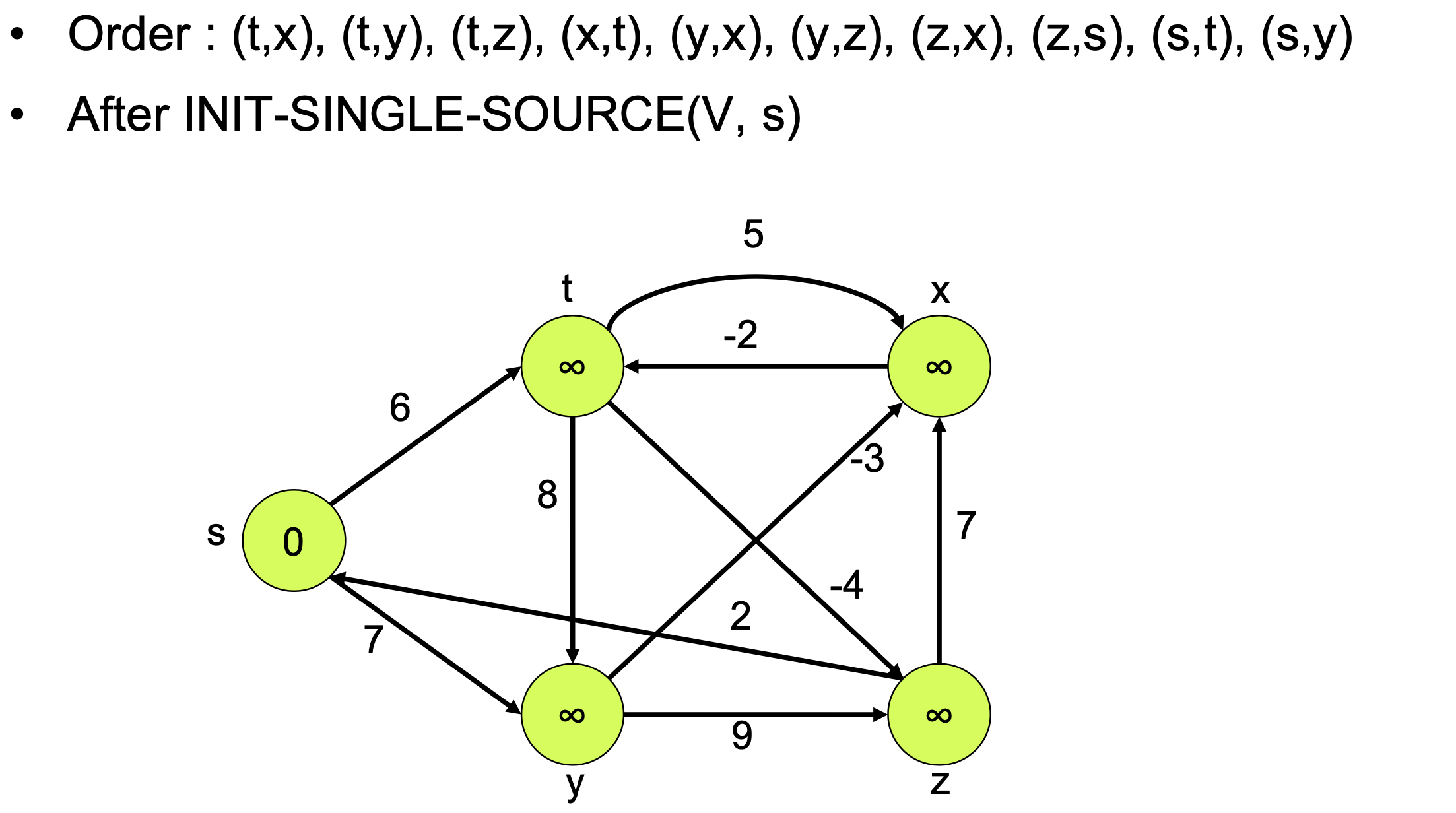

Neg. Weight Cycle Example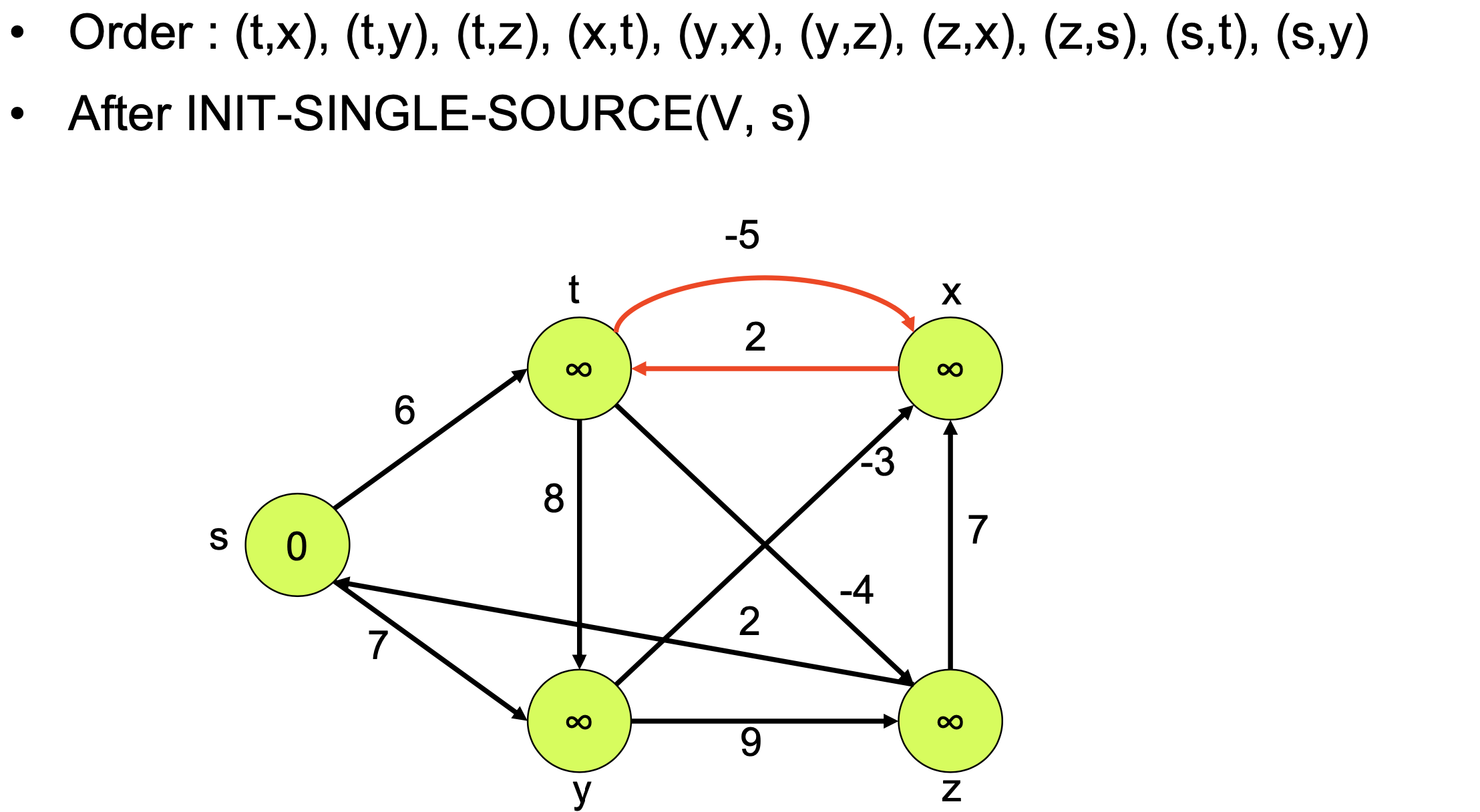➡️ d가 계속 작아지고 풀리지 path가 안나옴

[2] SSP in DAG

• Problem: finding shortest paths in DAG
  • Bellman-Ford takes Θ(VE) time ➡️ How can we do better?
  • Idea: use topological sort
    • Since it is a DAG, there are no cycles
    • Every path in a DAG is subsequence of topologically sorted, so processes vertices on each shortest path from left to right, then it would be done in one pass

Example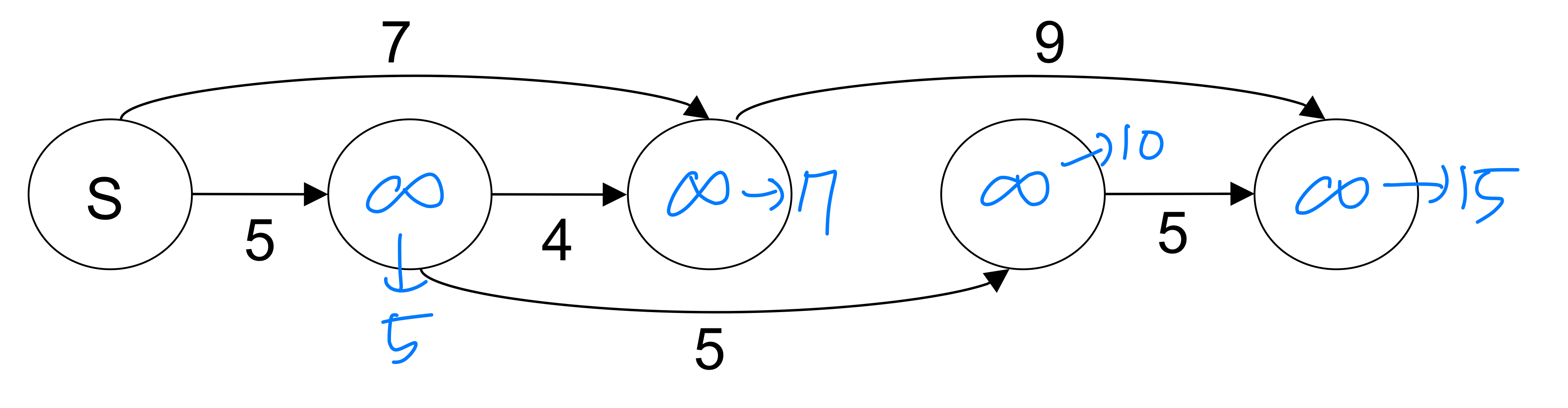

PseudocodeTime : Θ(V+E)

[3] Dijkstra’s Algorithm

• If there are no negative weight edge, we can beat(faster than) Bellman-Ford
• Similar to breadth-first search : weighted version of breadth-first search
  • Grow a tree gradually(서서히), advancing from vertices taken from a queue.
  • Instead of a FIFO queue, uses a priority queue
  • Keys are shortest-path weights (d[v])
    
    
• Have two sets of vertices :
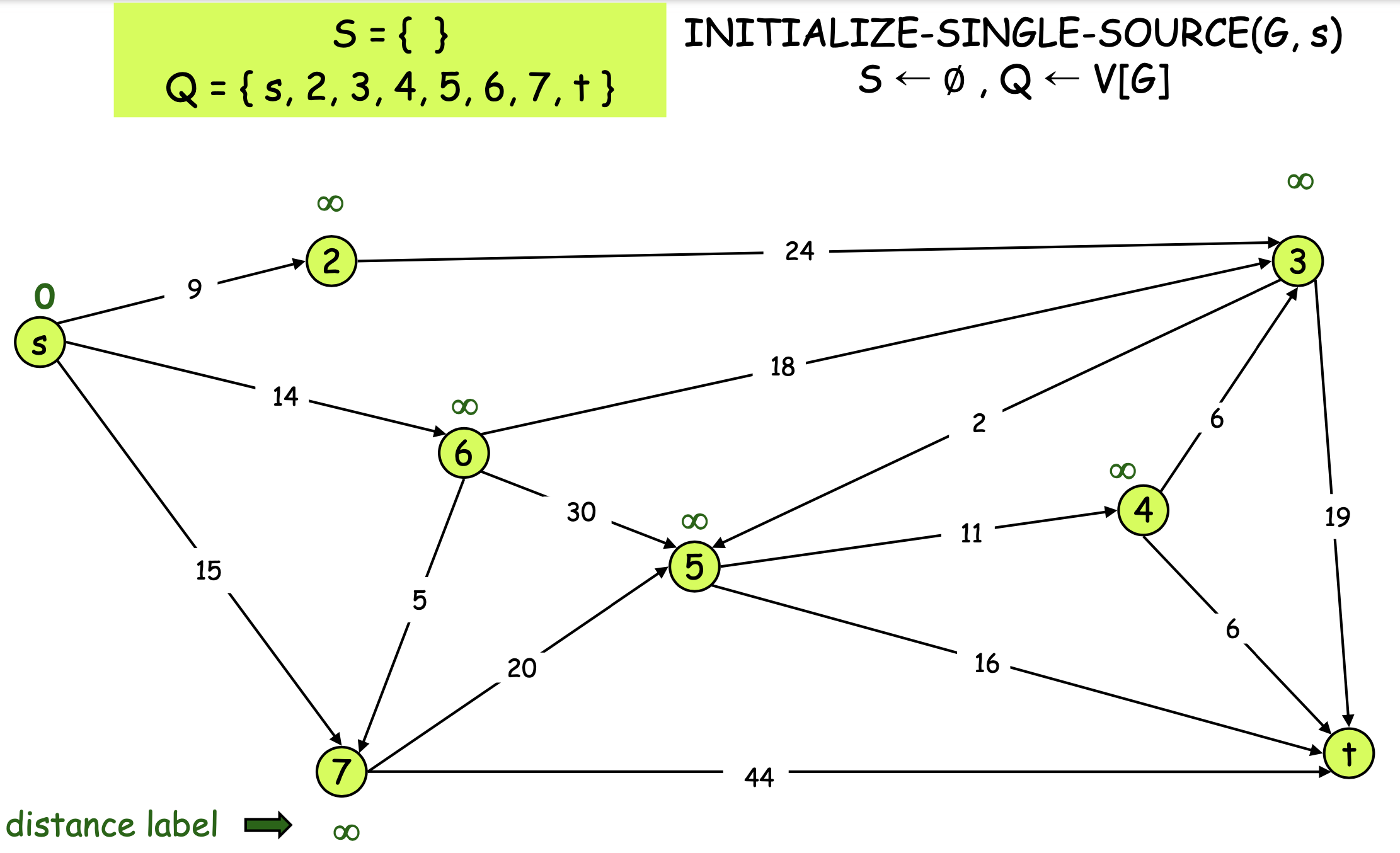
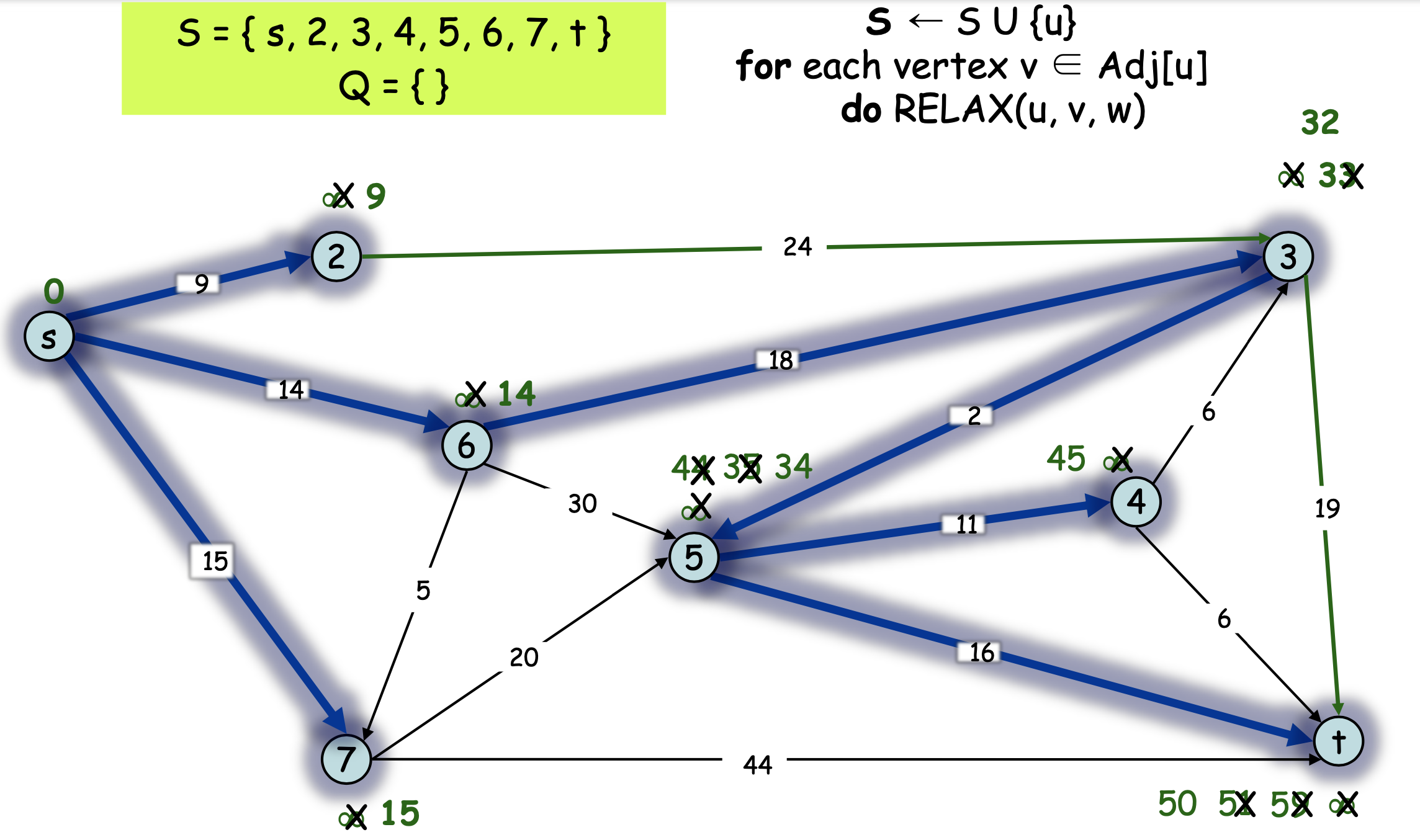
  • S = vertices whose final shortest-path weights are determined
  • Q = priority queue = V – S.
• For the graph G=(V,E), maintains a set S of vertices for which the shortest paths are known
• Repeatedly selects the vertex u (u ∈ V-S), with the minimum shortest-path estimated, adds u to S, and relaxes all edges leaving u
• What is the design strategy? ➡️ Greedy

---

Pseudo-code

---

Example - Find shortest path from s to t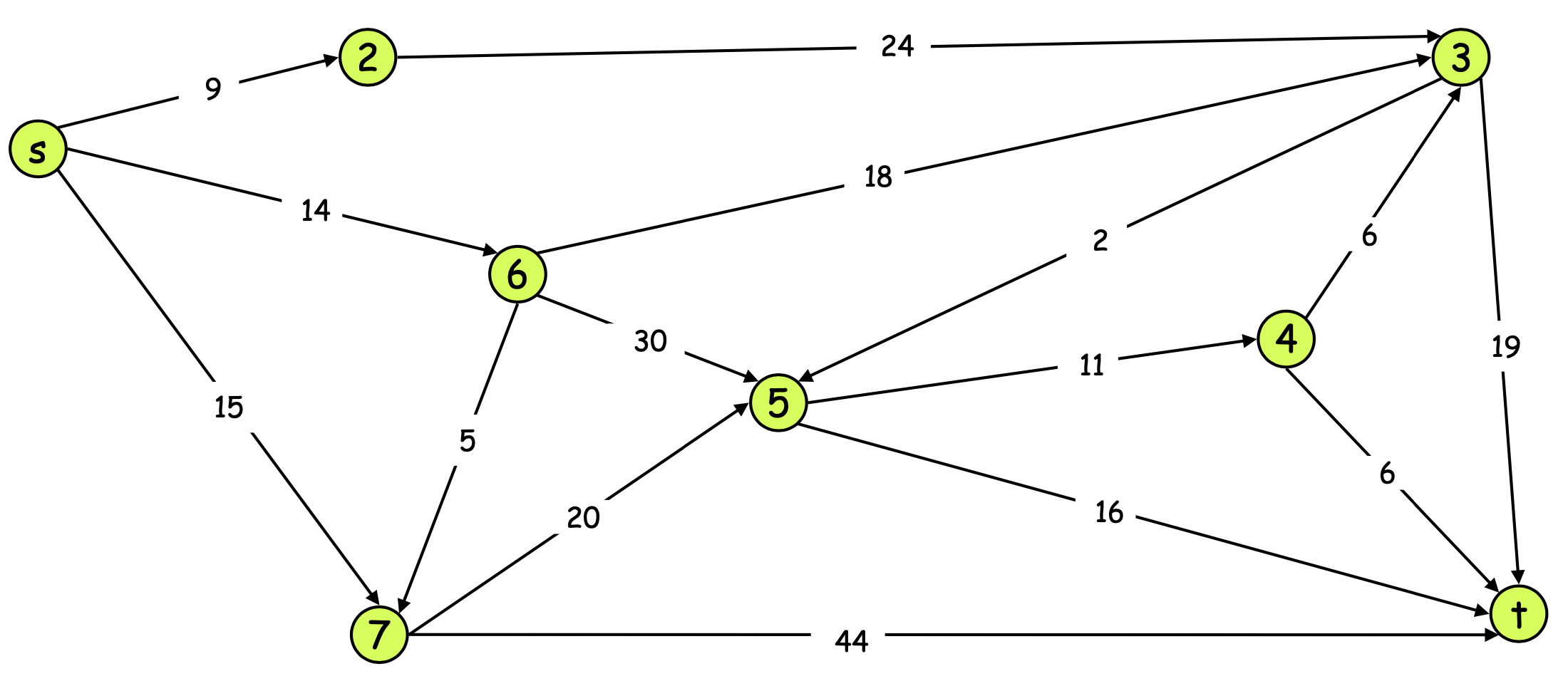

---

Correctness

• Theorem 24.6
  • loop invariant : At the start of each iteration of the while loop of lines 4-8, d[v] = $\delta$(s,v) for each vertex v ∈ S

---

Negative weight edge, Does not work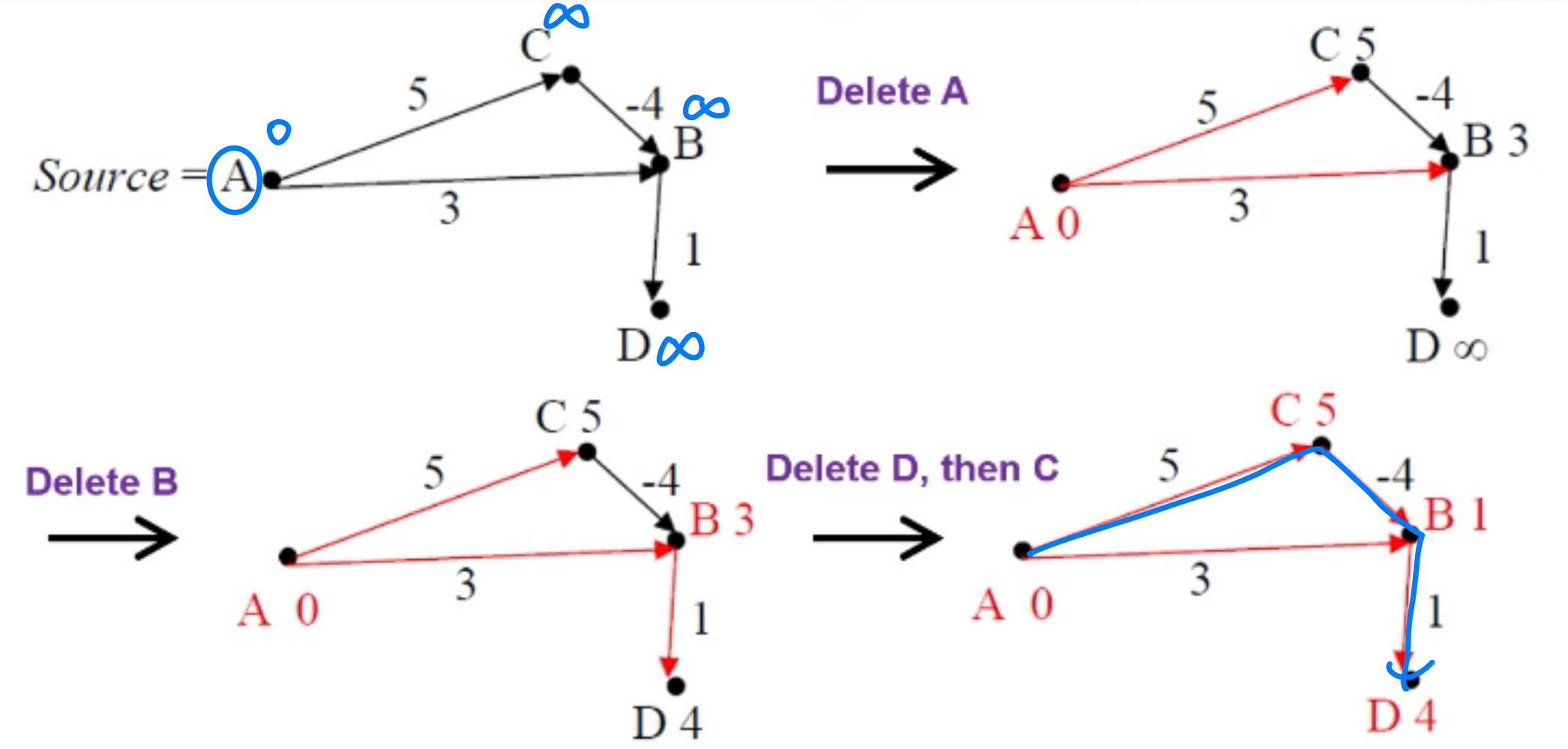

The glgorithm now terminates because the queue is empty. However, the path A→C→B→D has total length 5 + (-4) + 1 = 2 < 4; thus the length of the shortest path from the source A to D was not correctly evaluated

---

Time Analysis

• Like Prim’s algorithm, performance depends on implementation of priority queue
  • Binary heap :
    • Each operation takes O(lg V) time → O(E lg V)
  • Fibonacci heap :
    • O(V lg V + E) time

🖥️ All Pairs Shortest Path

Floyd - Warshall Algorithm

• The easiest way!
  • Iterate Dijkstra’s and Bellman-Ford |V| times(V번 반복)!

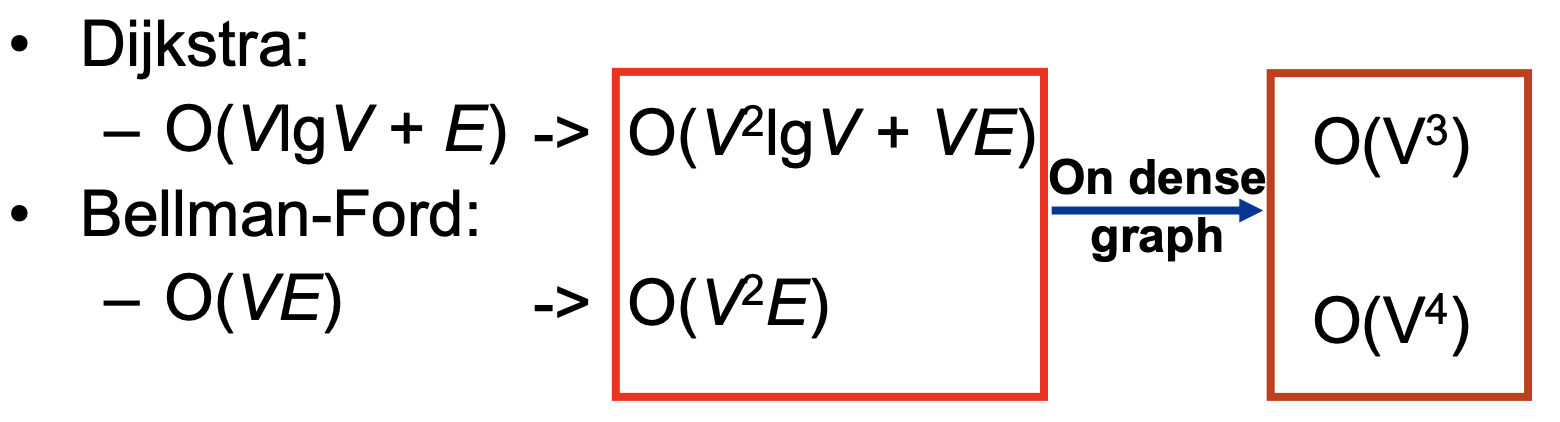→ Dense graph : E = O(V$^2$)

• Any other faster algorithms?
  • Floyd-Warshall Algorithm
    
    
• Negative edges are allowed
• Assume that no negative-weight cycle
• Dynamic Programming Solution
  • Optimal substructure

The structure of a shortest path

• Intermediate vertex
  • In simple path p = <v$_1$,...,v$_L$>, any vertex of p other than v$_1$ and v$_L$(제외), i.e., any vertex in the set {v$_2$,...,v$_{L-1}$}
• Key Observation
  • For any pair of vertices i, j in V.
  • Let p be a minimum-weight path of all paths from i to j whose intermediate vertices are all from {1,2,...,k}(중에 있다. 모두 path에 포함되는건 x) → Prob
  • Assume that we have all shortest paths from i to j whose intermediate vertices are from {1,2,...,k-1} → Subprob
  • Observe relationship between path p and above shortest paths(subprob)

Key Observation

• A shortest path does not contain the same vertex twice.
  • Proof: A path containing the same vertex twice contains a cycle(No simple path). Removing cycle give a shorter path.
    
    
• p is determined by the shortest paths whose intermediate vertices from {1,...,k-1}
• Case1: If k is not an intermediate vertex of p
  • Path p is the shortest path from i to j with intermediates from {1,...k-1} (without k)
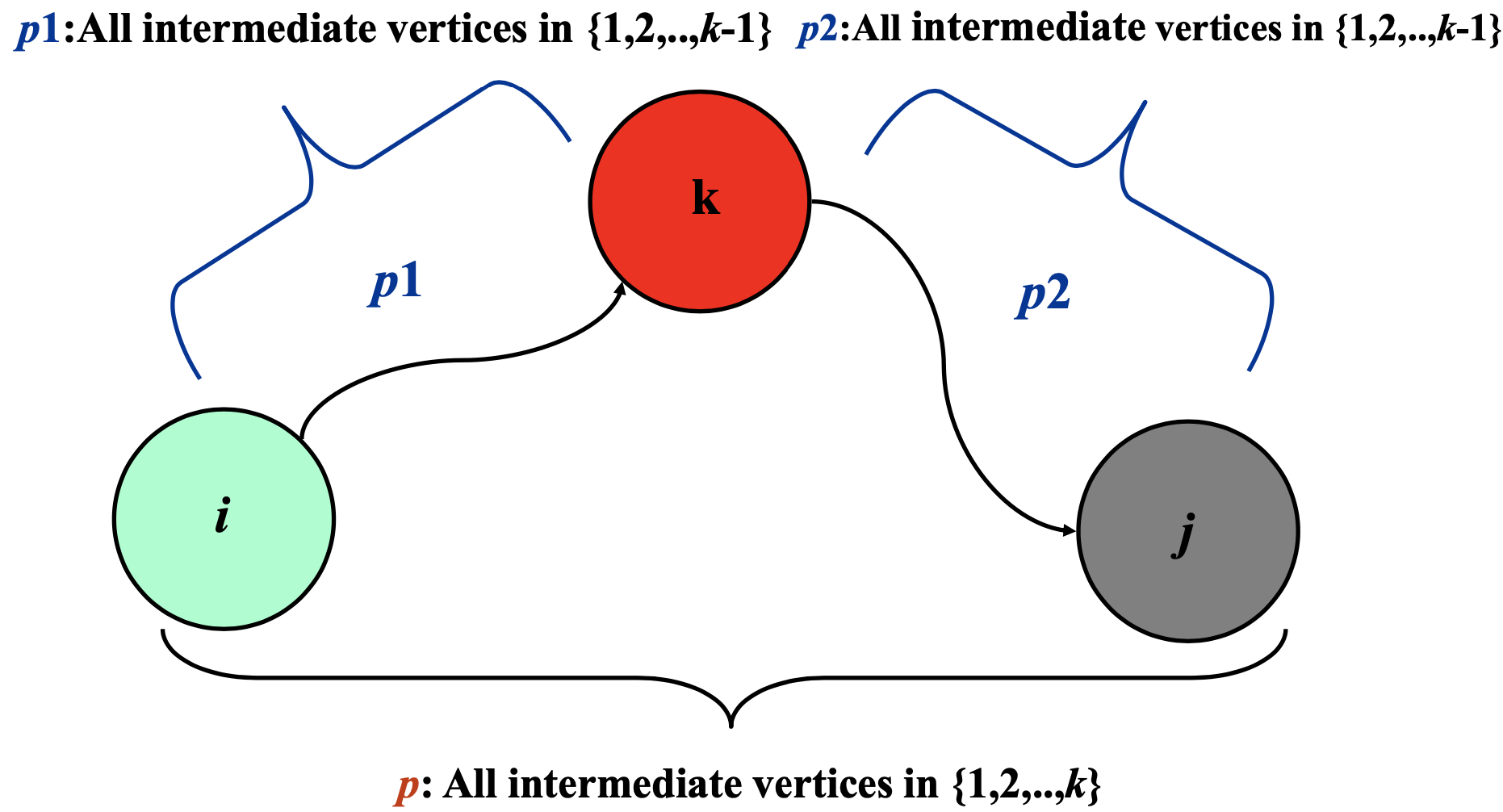
• Case2: If k is an intermediate vertex of path p
  • Path p can be broken down into i -- p1 → k - p2 → j
  • p1 is the shortest path from i to k with all intermediate vertices in the set {1,2,...,k-1}
  • p2 is the shortest path from k to j with {1,2,...,k-1}

A recursive solution

• Let d$_{ij}^{(k)}$ be the length of the shortest path from i to j such that all intermediate vertices on the path are in set {1,2,...,k}
  Ex_d$_{13}^{(4)}$ → 1, 2, 4, 3
• Let D(k) be the n Χ n matrix [d$_{ij}^{(k)}$]
• d$_{ij}^{(0)}$ is set to be w$_{ij}$ (no intermediate vertex).
• d$_{ij}^{(k)}$ = min(d$_{ij}^{(k-1)}$ , d$_{ik}^{(k-1)}$ + d$_{kj}^{(k-1)}$ ) (k≥1)
  → min(k가 intermediate vertex인 경우, 아닌경우)
• D(n) = (d$_{ij}^{(n)}$) gives the final answer, for all intermediate vertices are in the set {1,2,...,n} : d$_{ij}^{(n)}$ = δ(i,j) for all i,j ∈ V
  

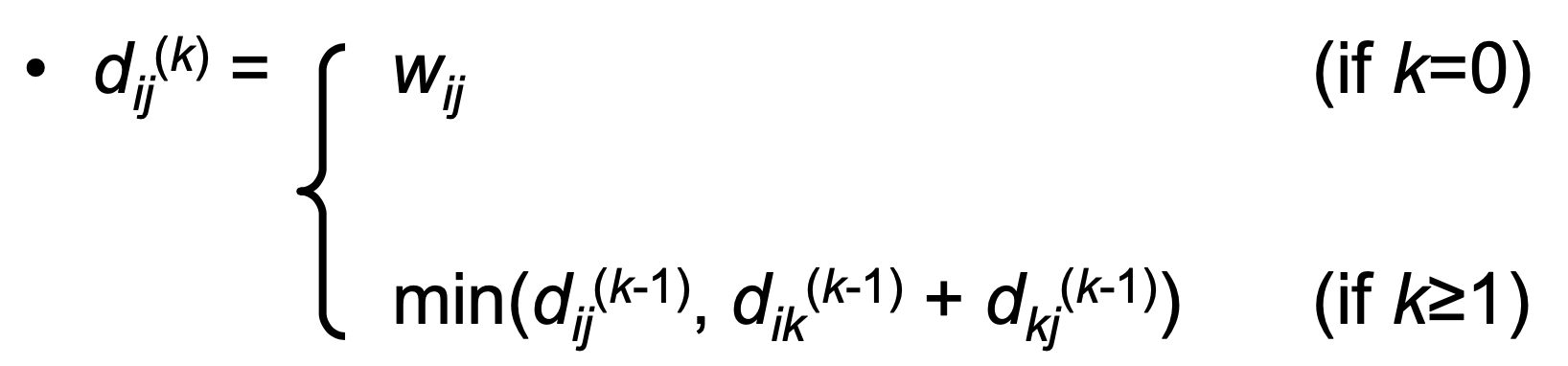
Extracting the Shortest Paths

• The predecessor pointers pred[i,j] can be used.
• Initially,
  • pred[i,j] = NIL (if i = j or w$_{ij}$ = $\infin$)
  • pred[i,j] = i (if i ≠ j or w$_{ij}$ < $\infin$)
• Whenever the shortest path from i to j passing through an intermediate vertex k is discovered, we set pred[i,j] = k
  
  
• Observation:
  • If pred[i,j] = NIL, shortest path does not exist
  • If there exists shortest path and the shortest path does not pass through any intermediate vertex, then pred[i,j] = i
  • If pred[i,j] = k, vertex k is an intermediate vertex on shortest path form i to j
    
    
• How to find?
  • If pred[i,j] = i, the shortest path is edge (i,j)
  • Otherwise, recursively compute
    (i , pred[i,j]) and (pred[i,j] , j)

Computing the weights bottom up

Example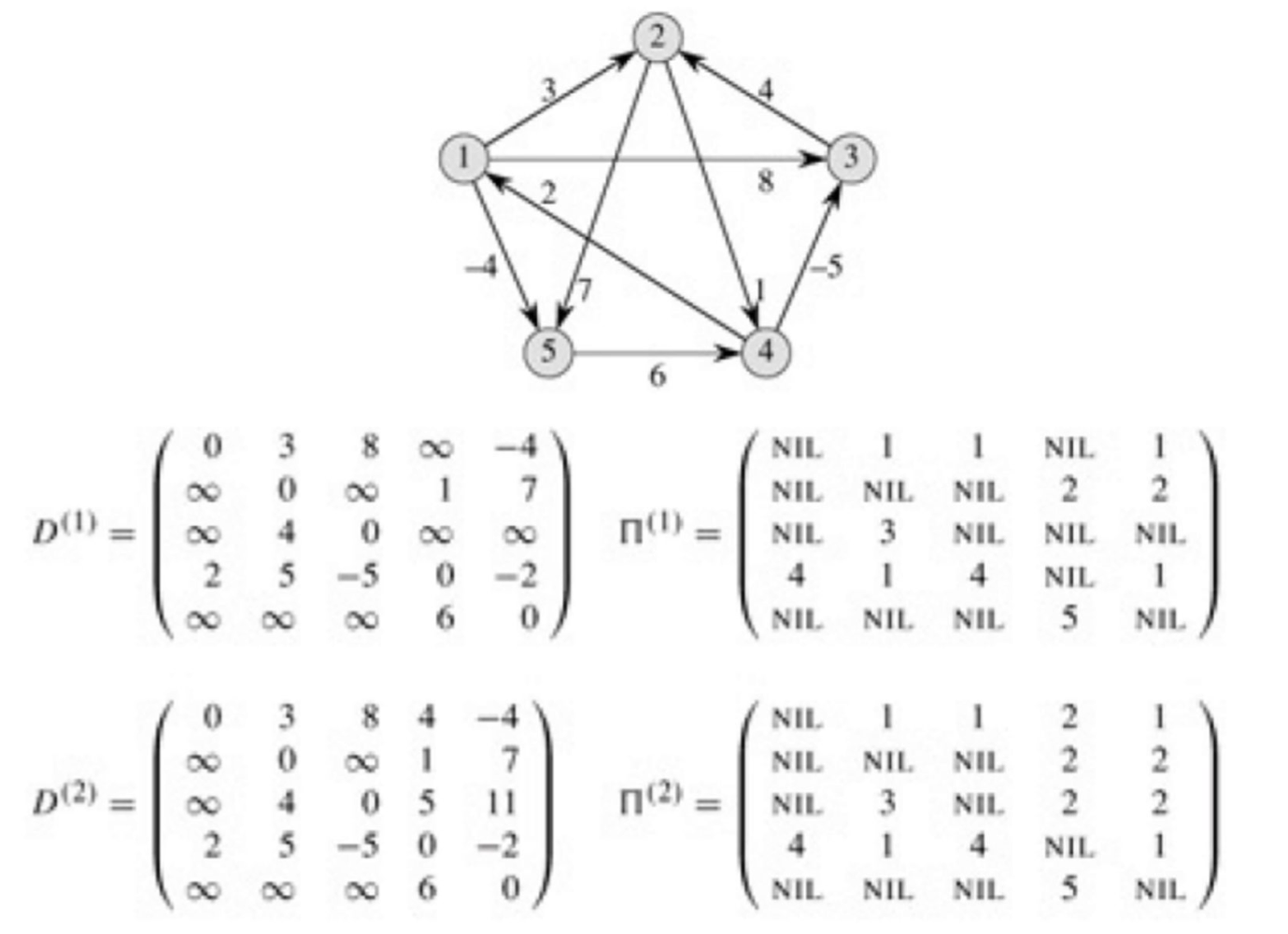

Exercise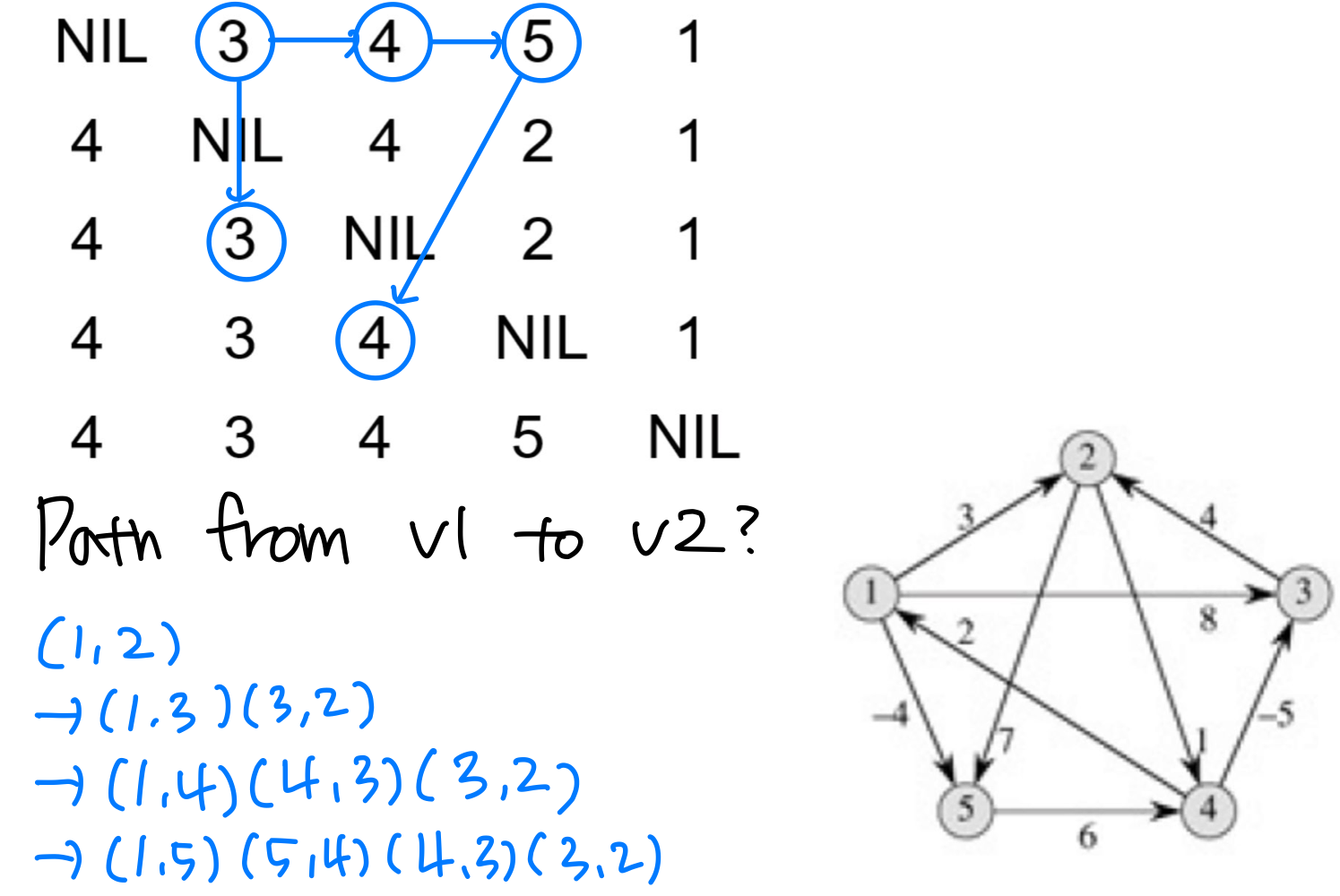

Analysis

• Θ(n$^3$) → Θ(|V|$^3$)
• Faster than previous algorithms
  O(|V|$^4$), O(|V|$^3$lg|V|)
• Problem: ⭐️ Space Complexity Θ(|V|$^3$)
• It is possible to reduce this down to Θ(|V|$^2$) by keeping only one matrix instead of n

Modified Version

Transitive Closure

• Given directed graph G = (V, E)
• Compute G$^*$ = (V, E$^*$)
• E$^*$ = {(i, j) : there is path from i to j in G}
• Could assign weight of 1 to each edge, then run FLOYD-WARSHALL
• If d$_{ij}$ < n, then there is a path from i to j
• Otherwise, d$_{ij}$ = $\infin$ and there is no path
  
  
• Using logical operations OR, AND
• Assign weight of 1 to each edge, then run FLOYD-WARSHALL with this weights.
  
  

---

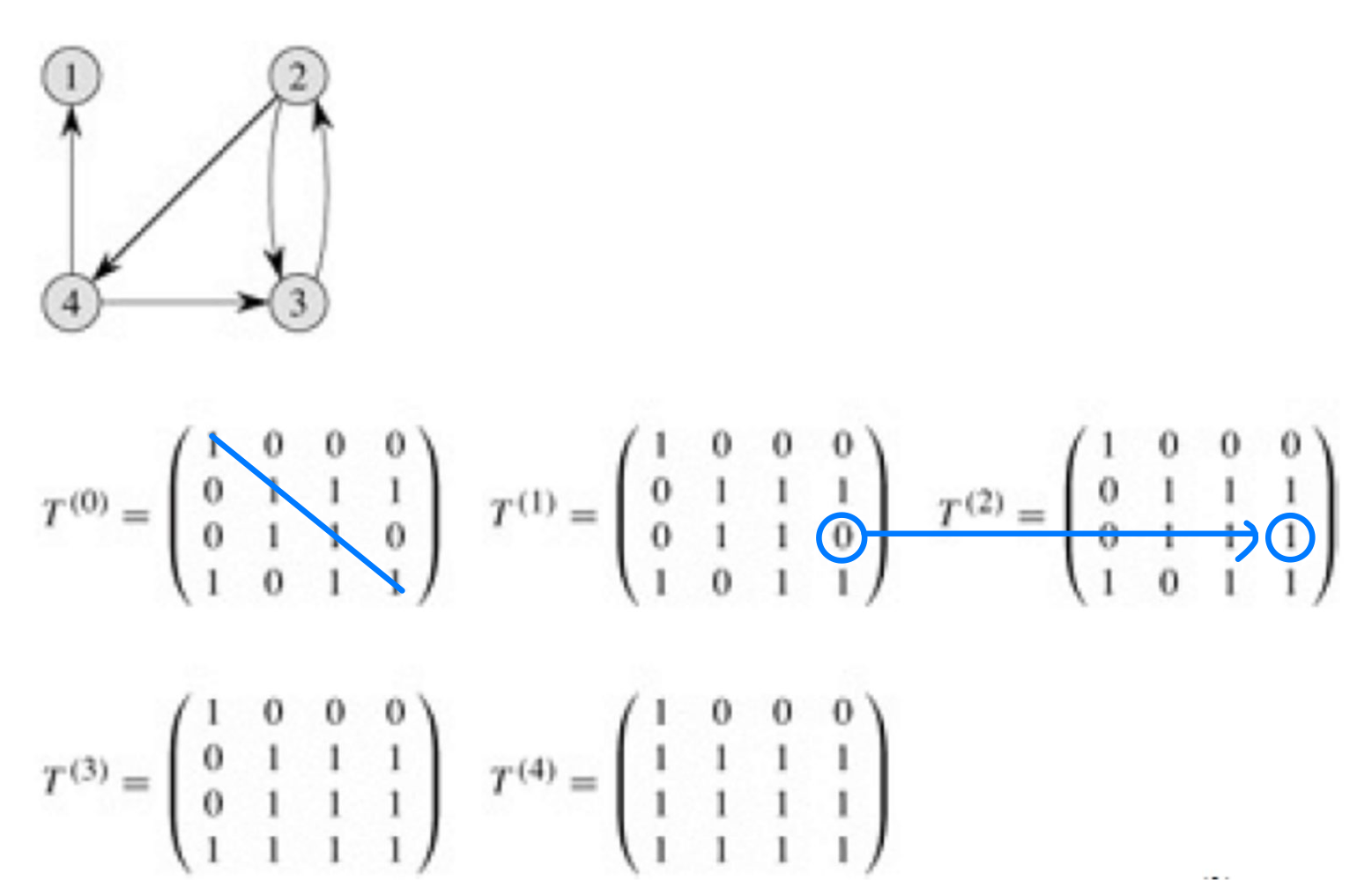
🖥️ Exercise in class

1. Dijkstra's algorithm

After vertex D is extracted from PQ and all edges incident from vertex D are relaxed, what is distance of B, C, E?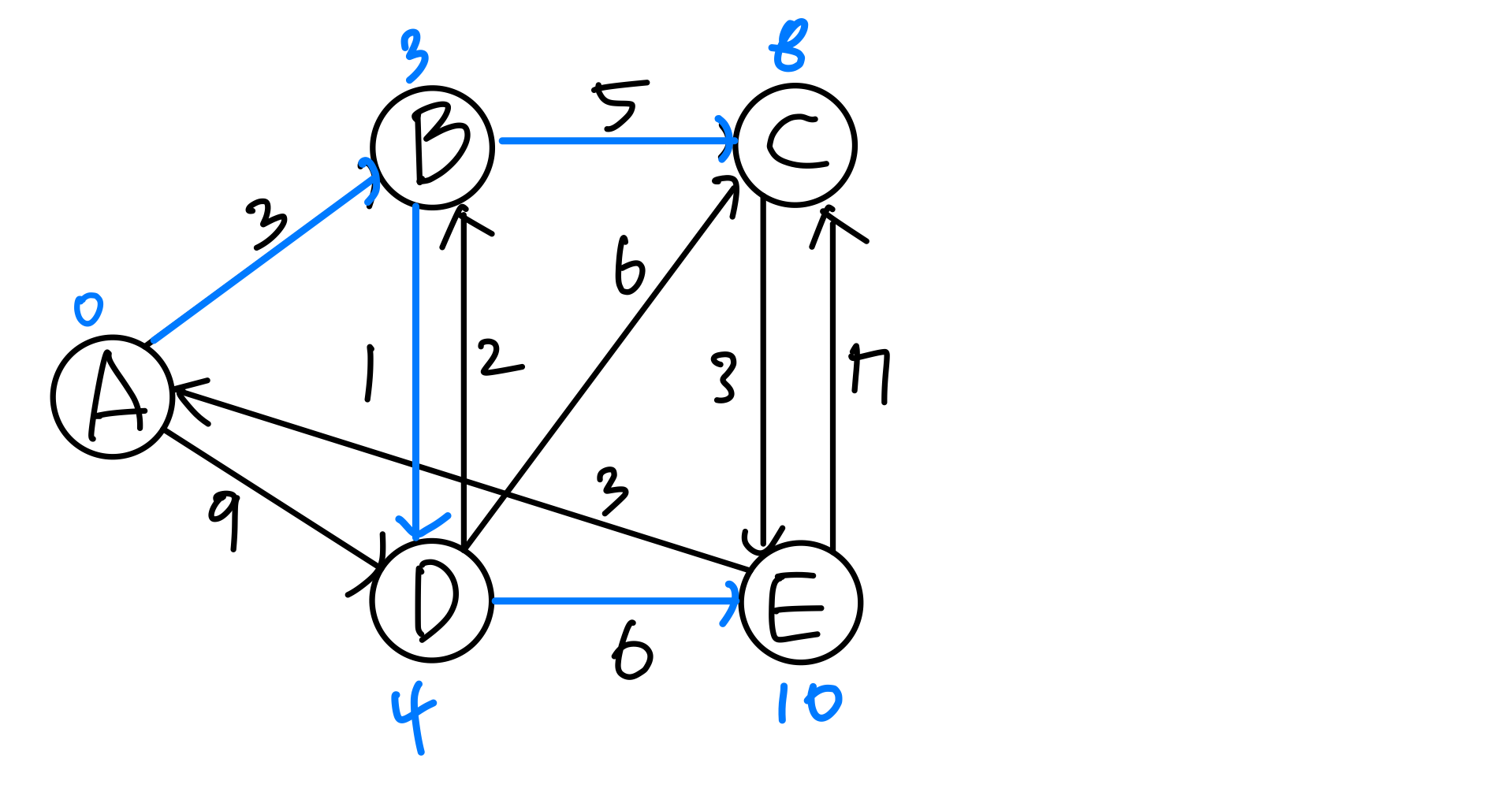➡️ B = 3(A), C = 8(B), E = 10(D)

2. Floyd's algorithm

→ DP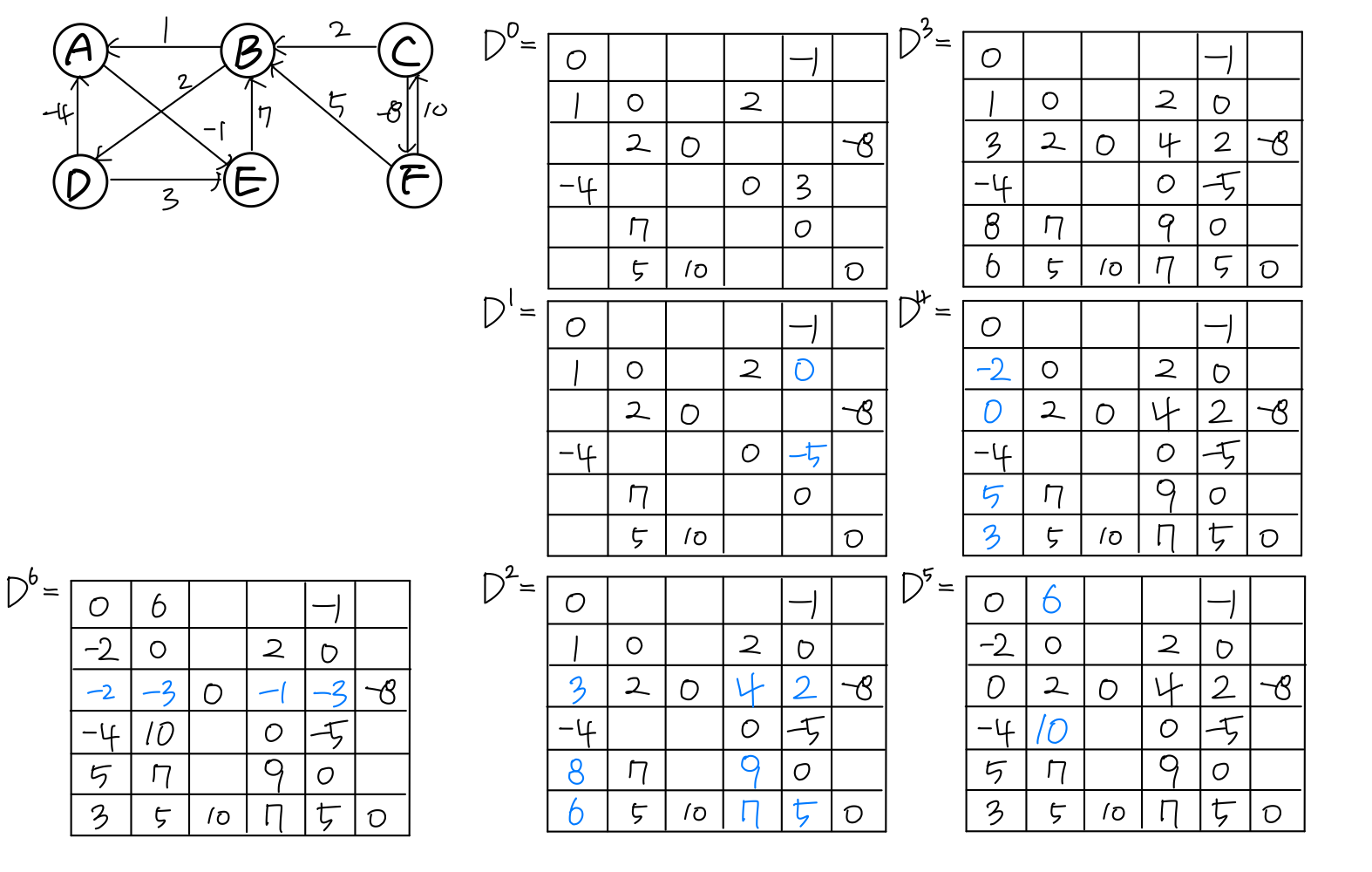

3. All pair shortest path

• SSP → All-pair
  • Dijkstra : $\Theta$(V$^3$)
  • Bellman-Ford : $\Theta$(V$^4$)
• Floyd : $\Theta$(V$^3$)
  ➡️ Time complexity 비슷, Why use Floyd?
  A. It can deal with negative edge
  

HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.