[ Algorithm ] 10. String Matching

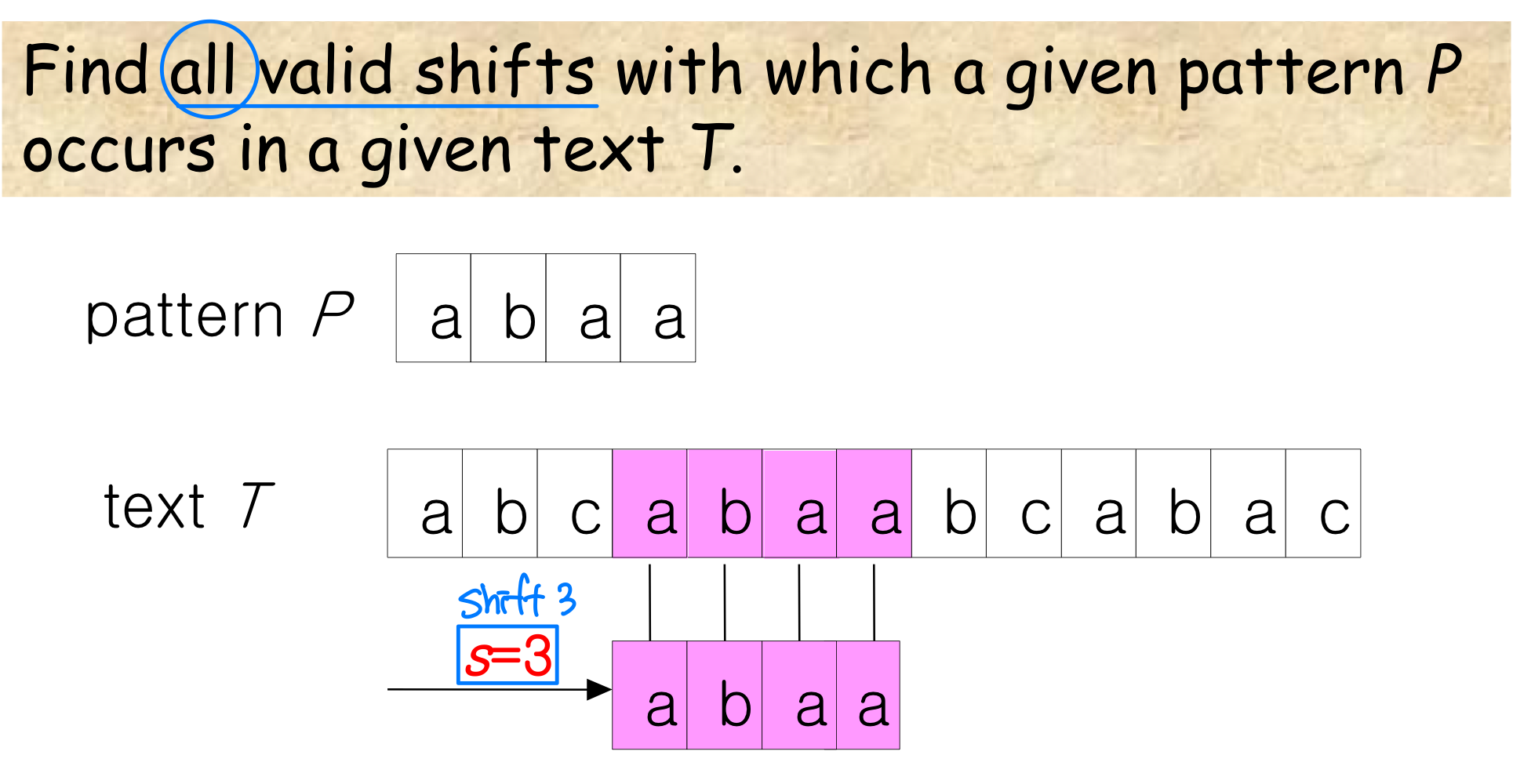
Notation and terminology

• T[1..n]: the text
• P[1..m]: the pattern
• P occurs with shift s in T if T[s+j] = p[j] for 1≤j≤m.
• If P occurs with shift s in T, then we call s a valid shift; otherwise, an invalid shift

[1] The naïve string-matching algorithm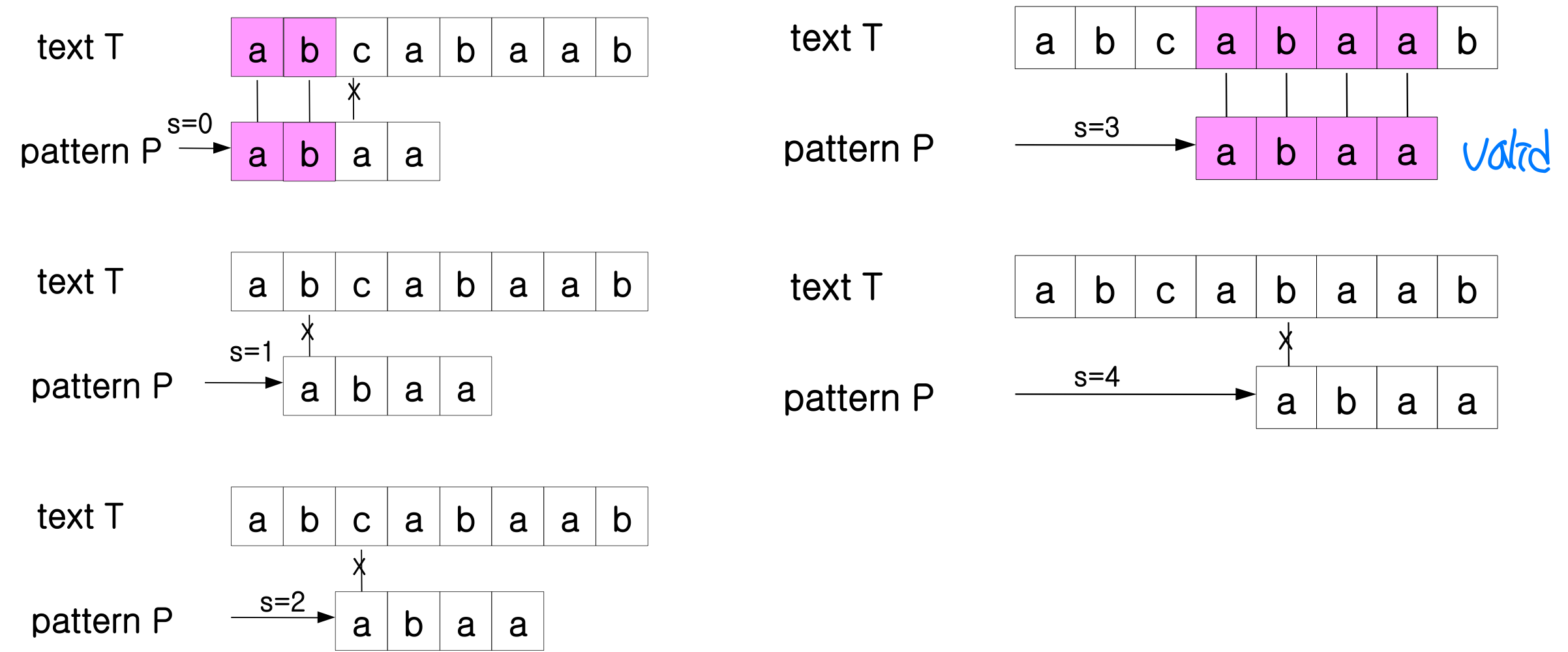

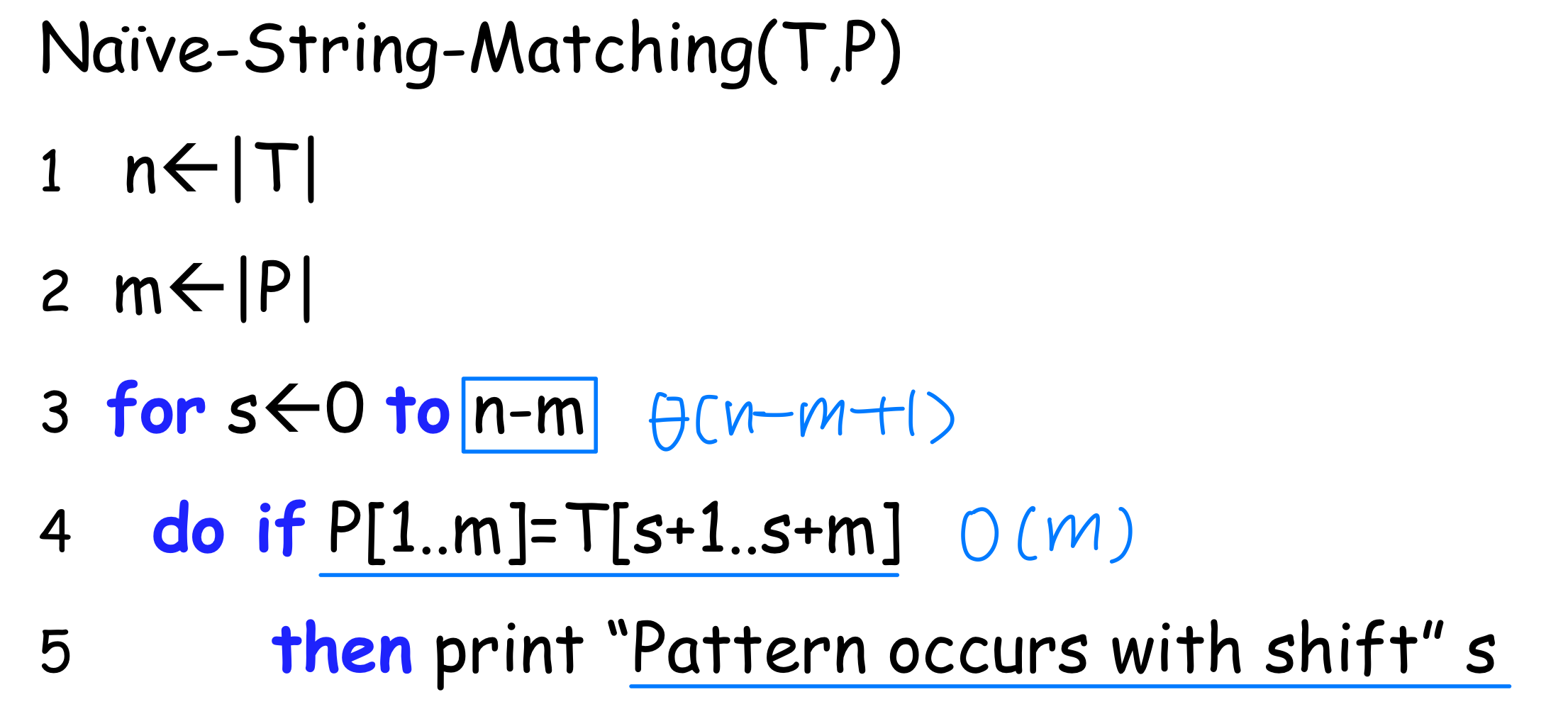
Problem in the naïve algorithm

• O((n-m+1)m) time → if m = n / 2, O(n$^2$)
• The naïve string matching is inefficient because information gained about the text for one value of s is entirely ignored in considering other values of s.
  • If P = aaab and we find s = 0 is valid, then none of the shifts 1, 2, or 3 are valid → 1, 2, 3 are invalid

[2] Rabin-Karp algorithm

• Main Idea
  : length m string is regarded as m digits radix-d number.
• P[1..m] : Convert it into m-digit number p
• Substring T[s+1..s+m] : Convert it into m-digit number ts
  Ex) ∑={0,1,2,...,9}, P[1..m] = 31425,
  ➔ p = 31,425
• If p = t$_s$, then string matching!
• String matching problem
  ➔ is converted into number comparison problem

Example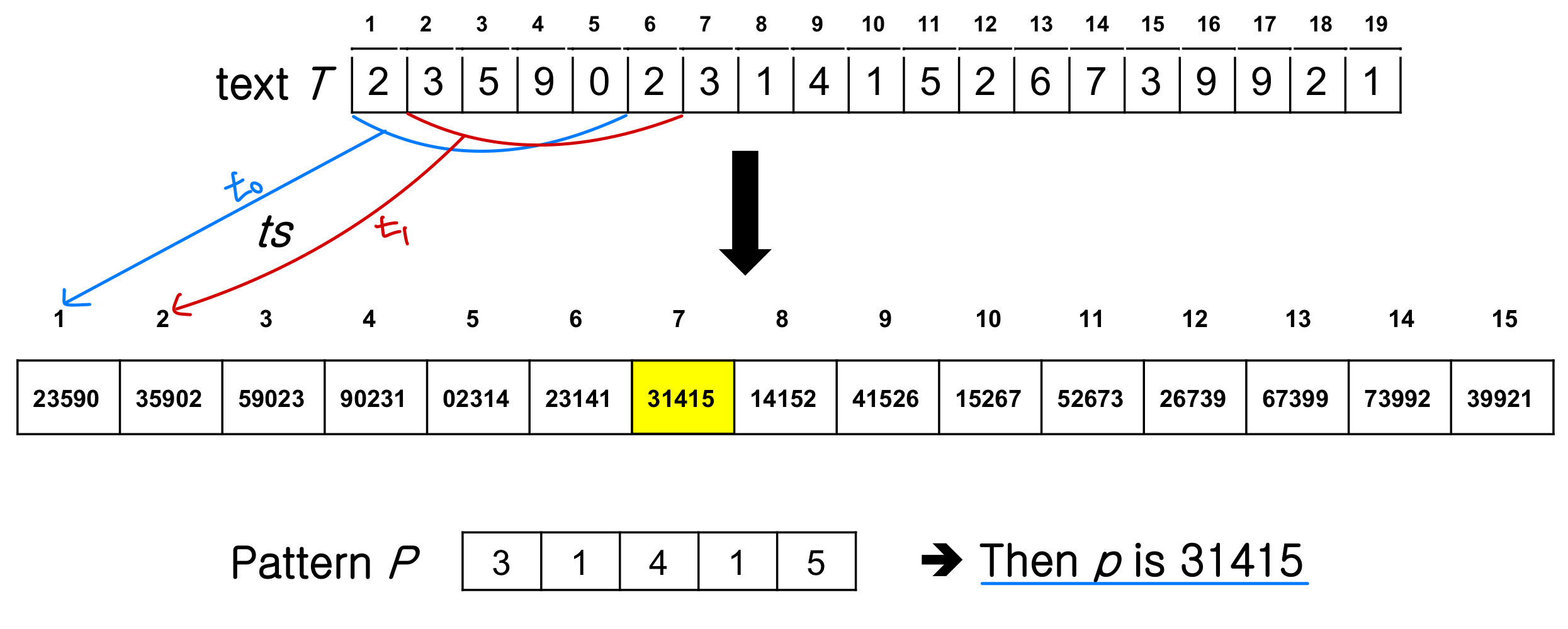

Convert string into number

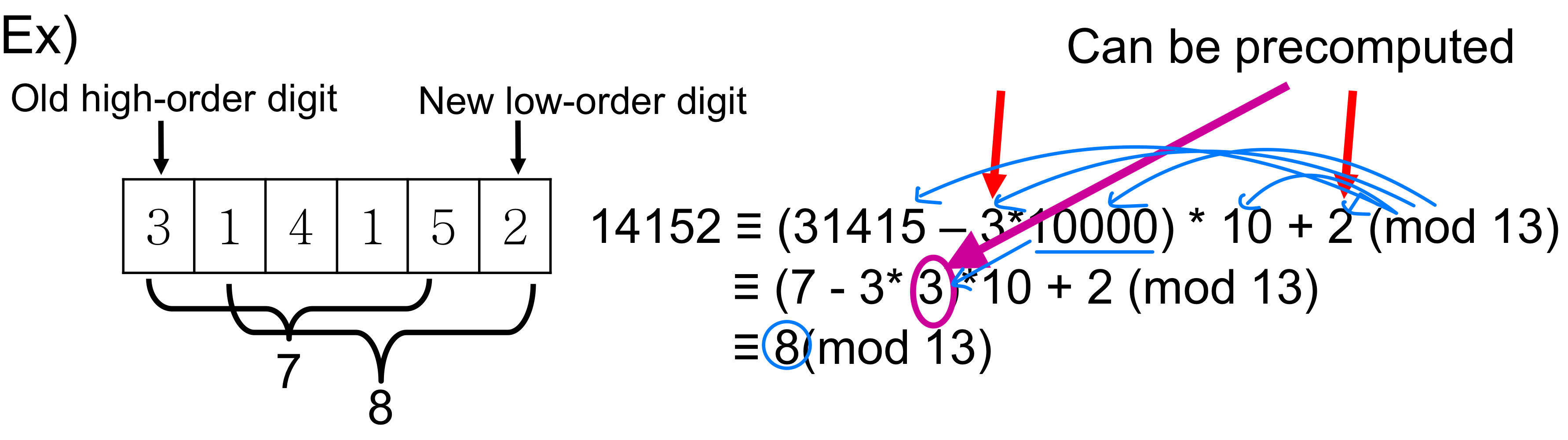
• Use Horner’s rule
  p = P[m] + 10(P[m-1]+10(P[m-2]+....+10(P[2]+10P[1])...))
• Ex) When P[1..m] = 31425, → Ө(m)
  p= 5+10(2+10(4+10*(1+10*3))) = 31,425
  → What if $\Sigma$ = {a, b ... z} : *10 → *26
• Is there faster way to calculate t$_s$?
  
  
• Calculate t$_0$ similarly.
  Then, we can calculate t$_{s+1}$ from ts
  • t$_{s+1}$ = 10(t$_s$-10m-1T[s+1])+T[s+m+1]
  • i.e., remove high order digit T[s+1] and bring low order
    digit.
• Ex) When t$_s$ = 31415 and T[s+5+1]= 2, → Text = ... 314152 ...
  t$_{s+1}$ = 10(31415 – 10000*3) +2 = 14152 → Ө(1)
  Computing p & t$_0$ : Θ(m)
  Computing t$_1$, ...t$_{n-m}$ : Θ(n-m) or Θ(n)
  → Ө(1) n-m개 ( n - m + 1(t$_0$) )

Comparing p with t$_s$

• How long will it take to compare p with t$_s$?
  • Constant time if m is very small
  • Otherwise ... → constant time이라고 할 수 없다
• Cure for the problem : Use ‘modulo’ operation.
  When comparing two numbers, we do not compare the numbers directly. Instead, take ‘modulo q’ operation and compare.
• However,the solution of working ‘modulo q’ is not perfect, since t$_s$ ≡ p (mod q) does not imply t$_s$ = p.
  • Valid : t$_s$ ≡ p (mod q) and t$_s$ = p
  • Spurious hit : t$_s$ ≡ p (mod q) but t$_s$ ≠ p
  • However, if t$_s$ ≠ p (mod q) , there is no chance that t$_s$ = p.
• Ex) 67399 != 31415 but, 67399 ≡ 31415 (mod 13)

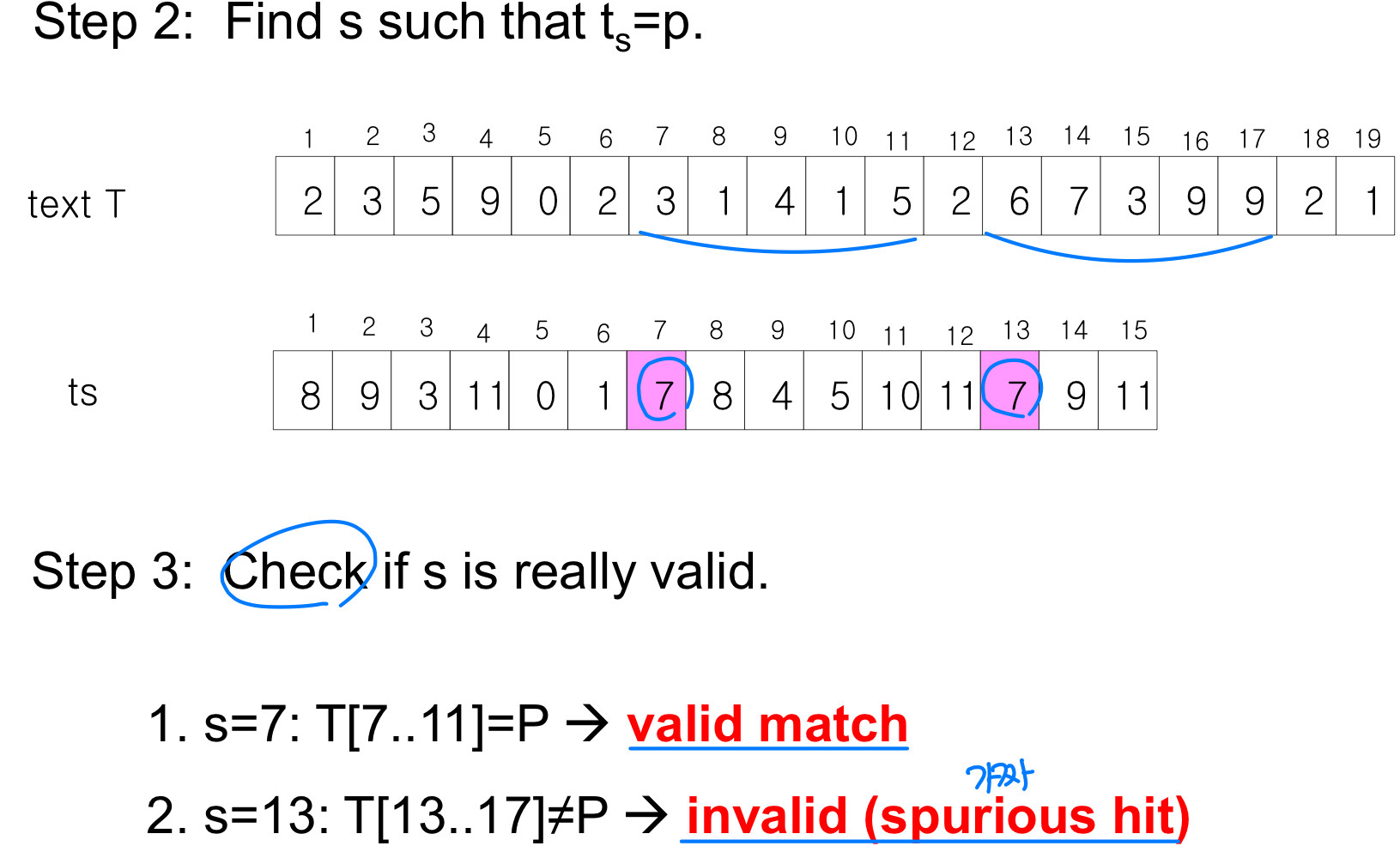
Algorithm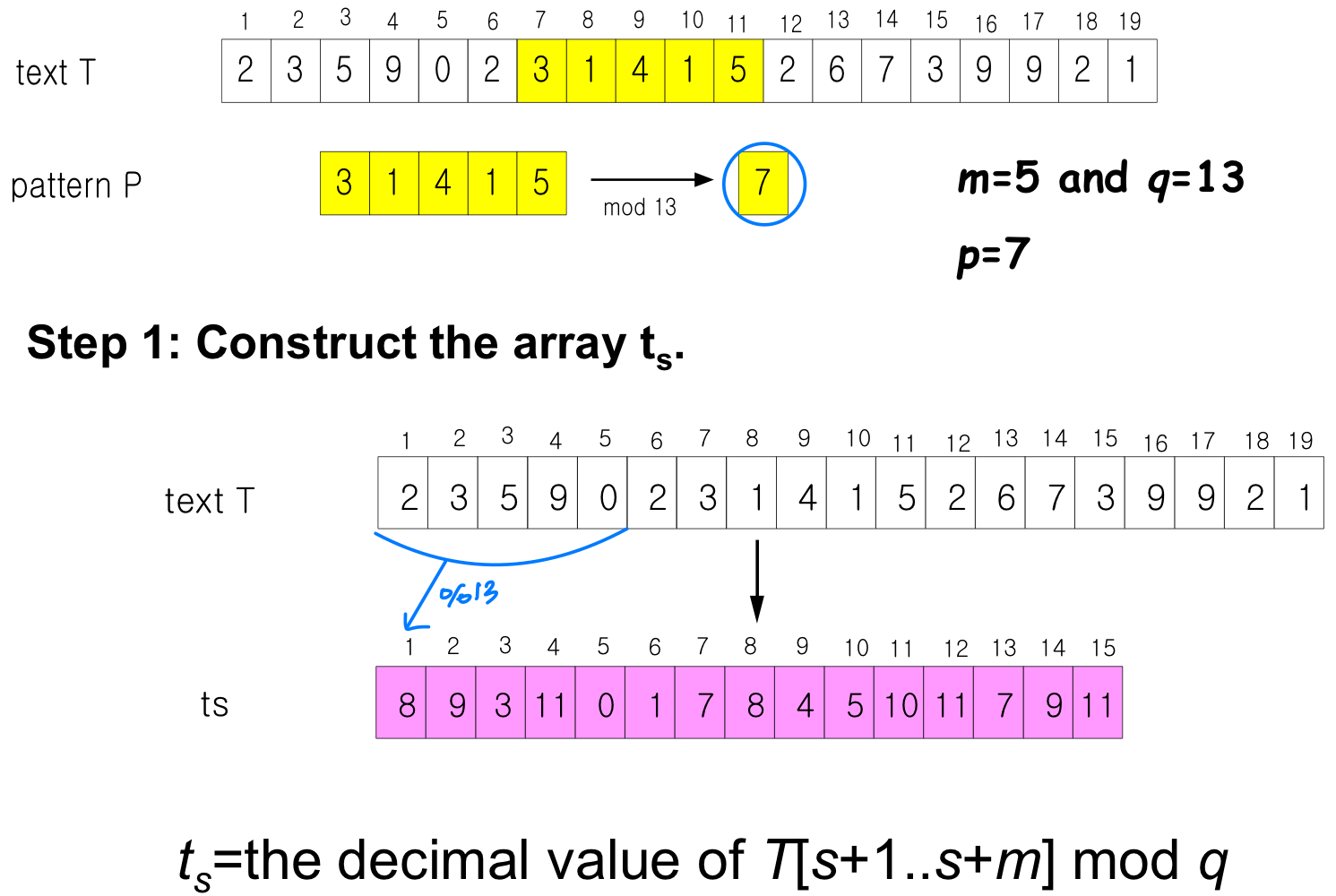

Modulo operation

• q : The modulus q is typically chosen as a prime number such that d*q just fits within one computer word in d-ary alphabet.
• Recalculation of p and t
  • p = original p (mod q)
  • t$_{s+1}$=(d(t$_s$ - T[s+1]h) + T[s+m+1]) (mod q) → Ө(1)

→ Constant time

Analysis

• Θ(m) preprocessing time --- calculation of p and t$_0$
• Θ((n-m+1)m) worst-case running time → 모두 mod q 값이 동일
  • Θ(n-m+1) times to find all s such that p = t$_s$
  • Θ(m) time to check if each s is really valid
  • However we expect few valid shifts
    → 그러나 유효한 변화가 거의 없을 것으로 예상, 실제로는 worst보다 빠를 것이다

[3] String matching with finite automata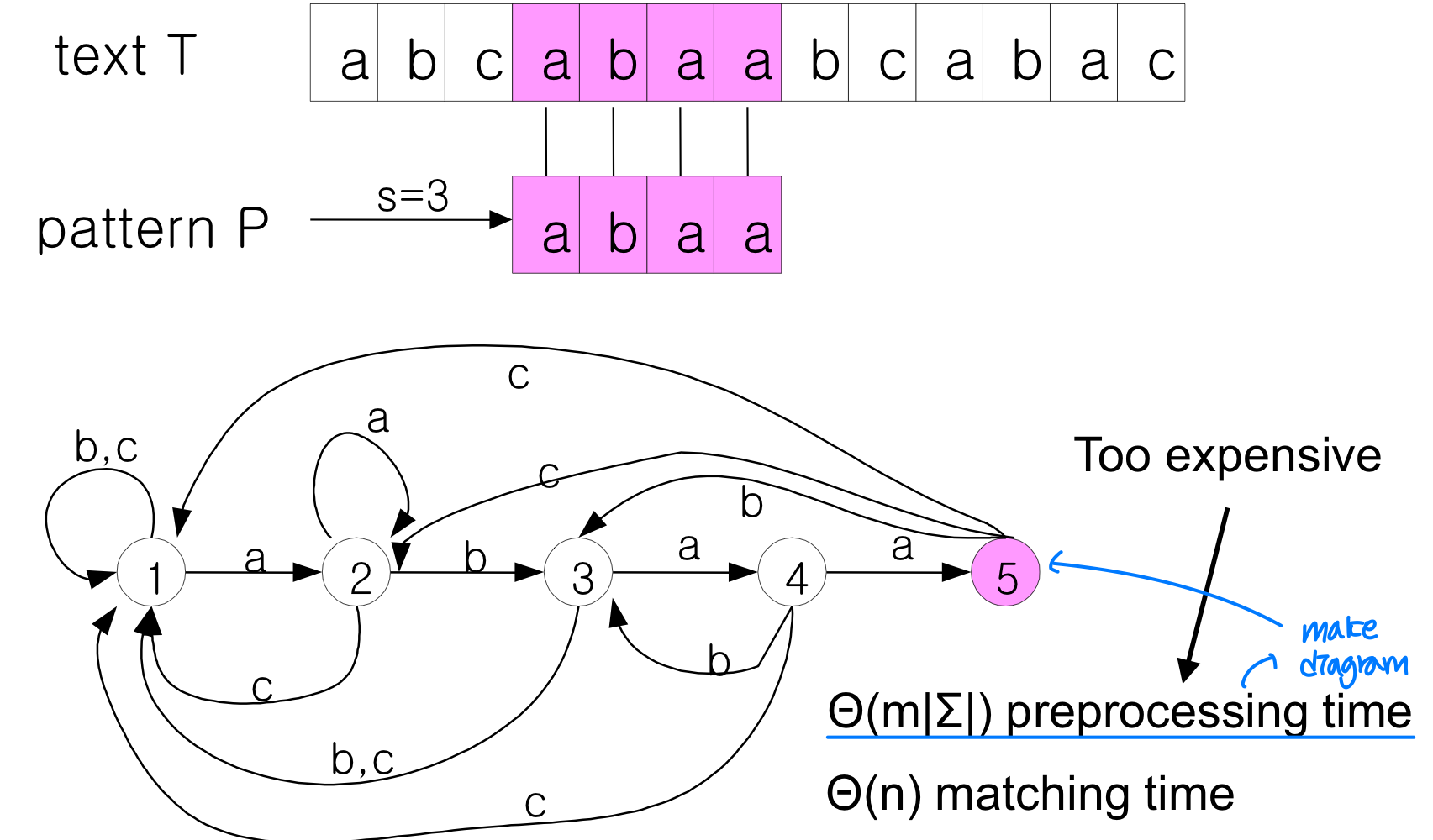

[4] Knuth-Morris-Pratt Algorithm

• Consider the operation of the naïve string matcher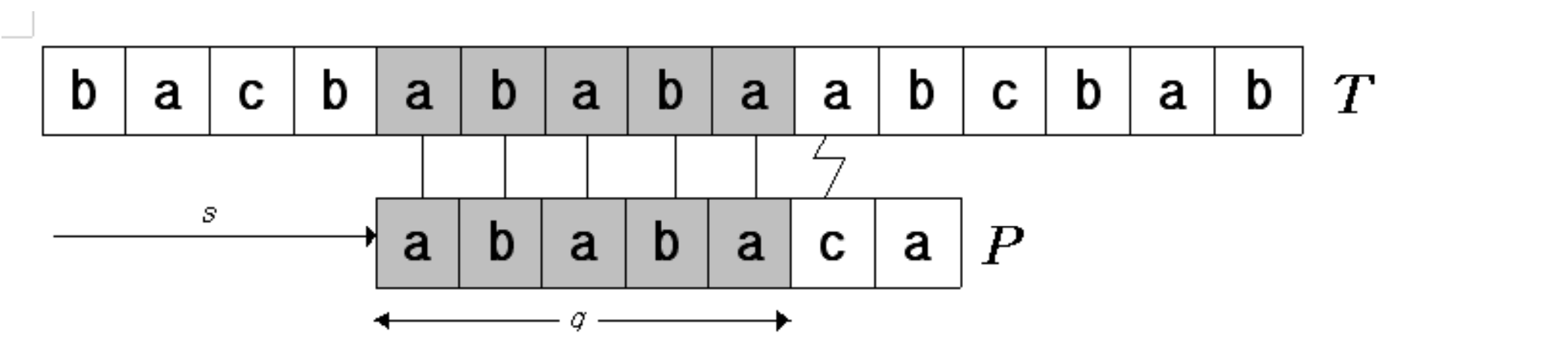When 6th pattern character fails to match the corresponding text character, where can we resume the match again?
  
  
• We don’t have to resume the match from the character right next to it!
  
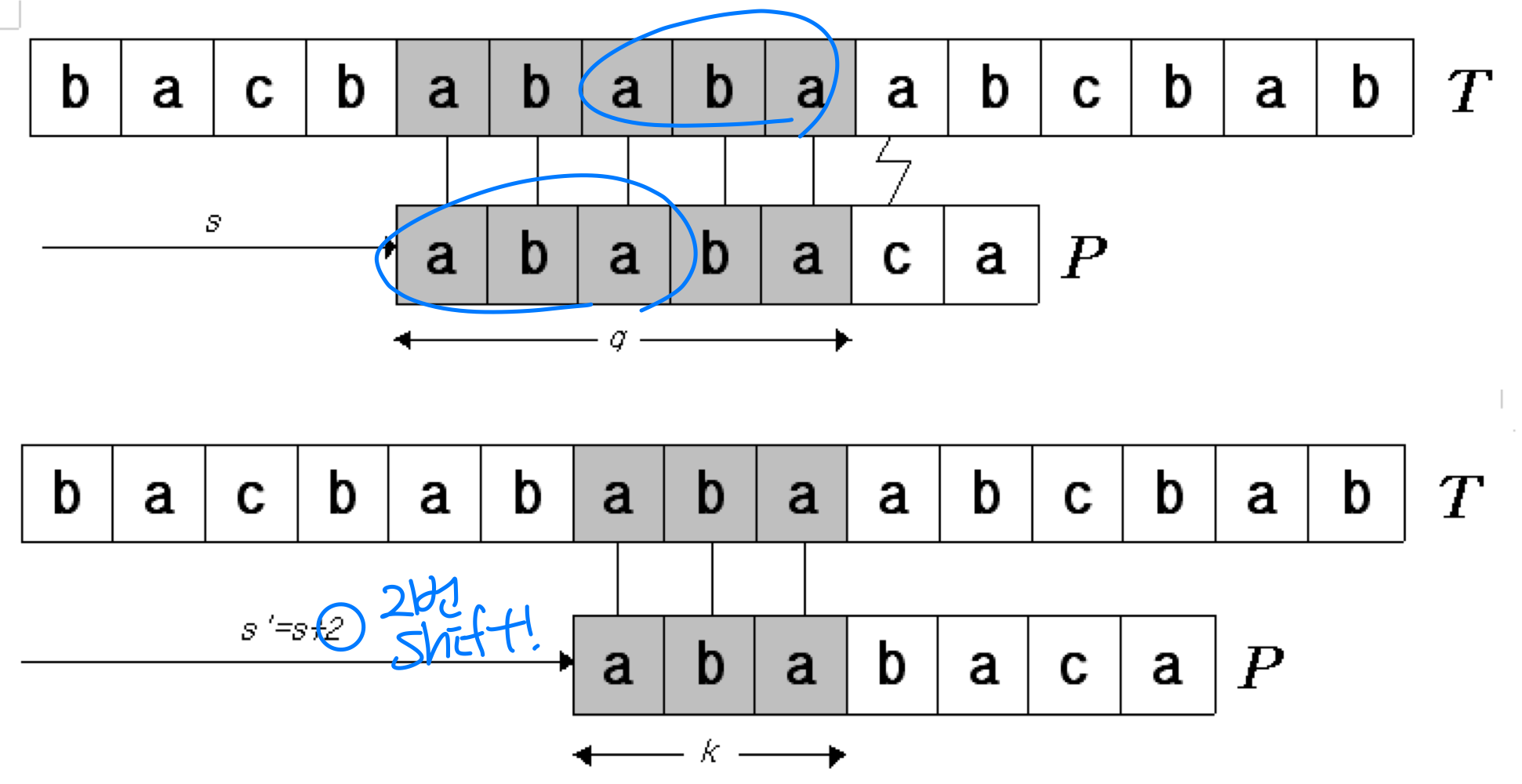
• In general, it is useful to know the answer to the following question :
  Given that pattern characters P[1..q] match text characters T[s+1..s+q], what is the least shift s’ > s such that
  P[1..k] = T[s’+1..s’+k], where s’ + k = s + q?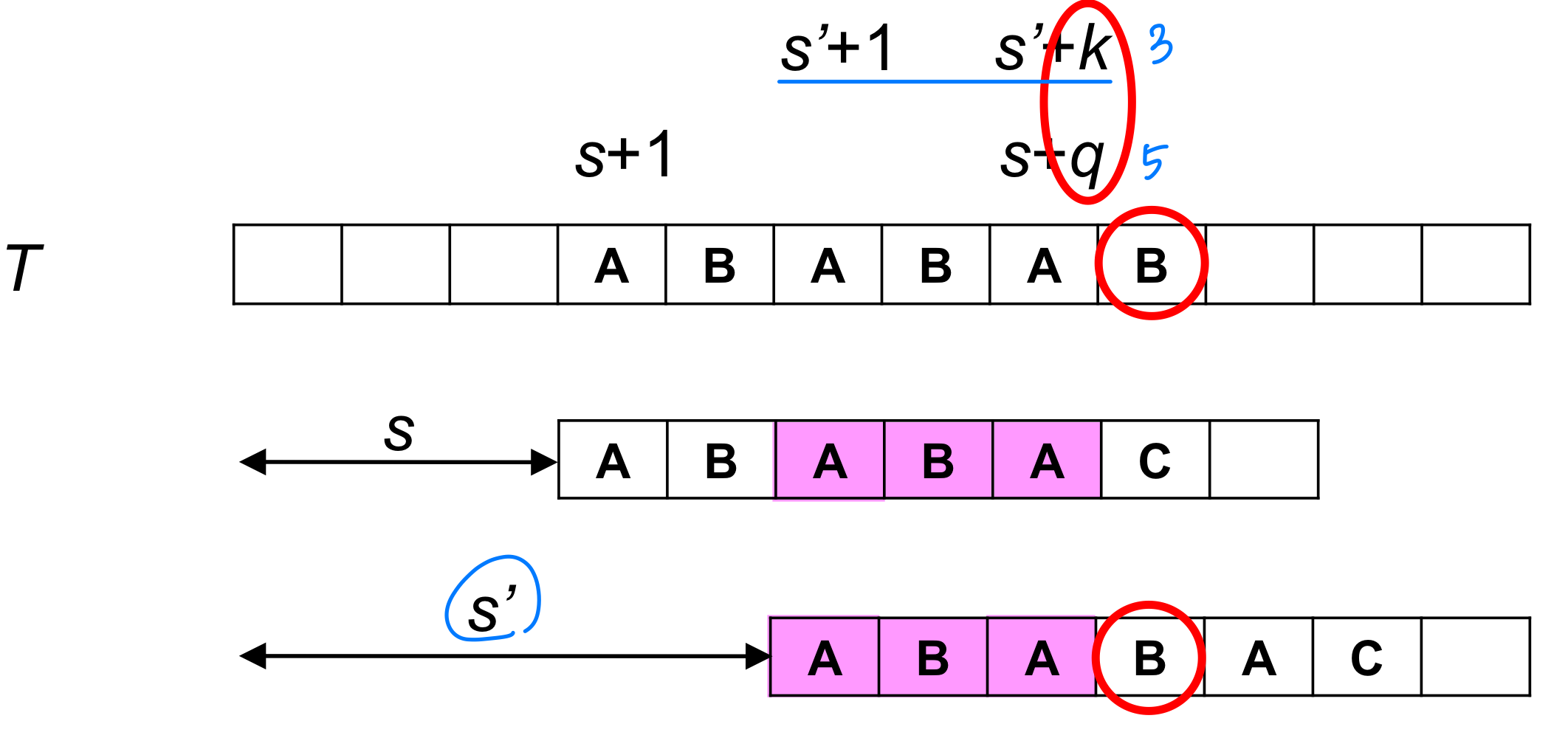
  
• The necessary information can be precomputed by comparing the pattern against itself
  → Text 필요 x, Pattern으로 비교 가능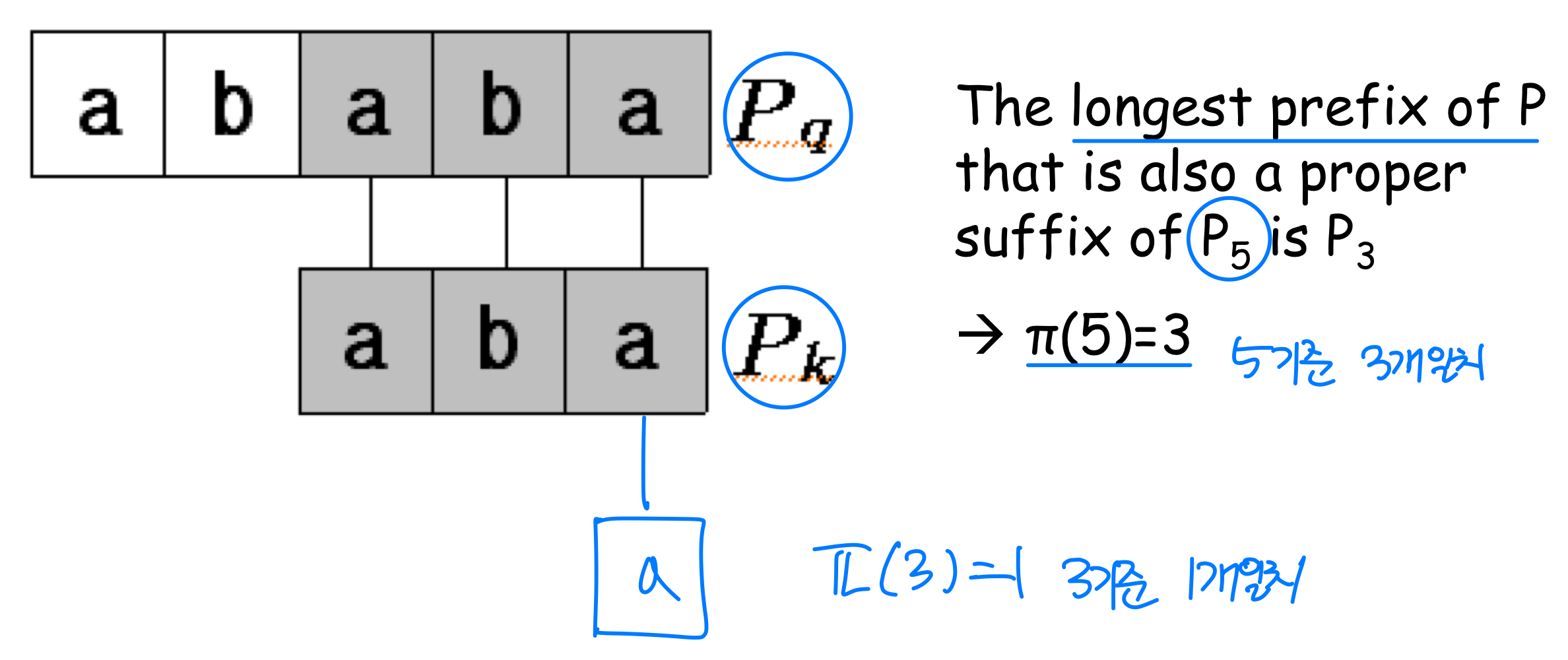

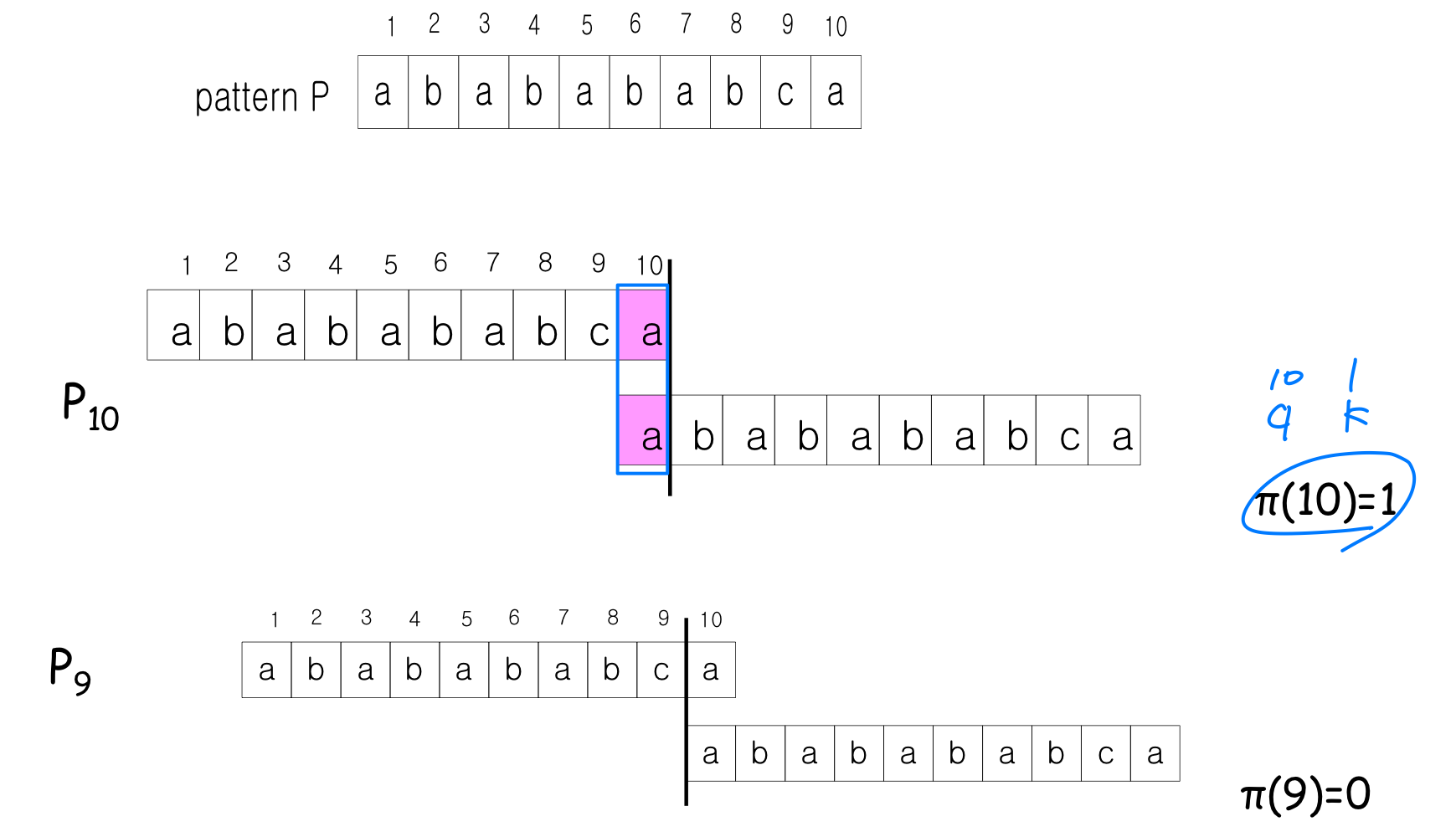
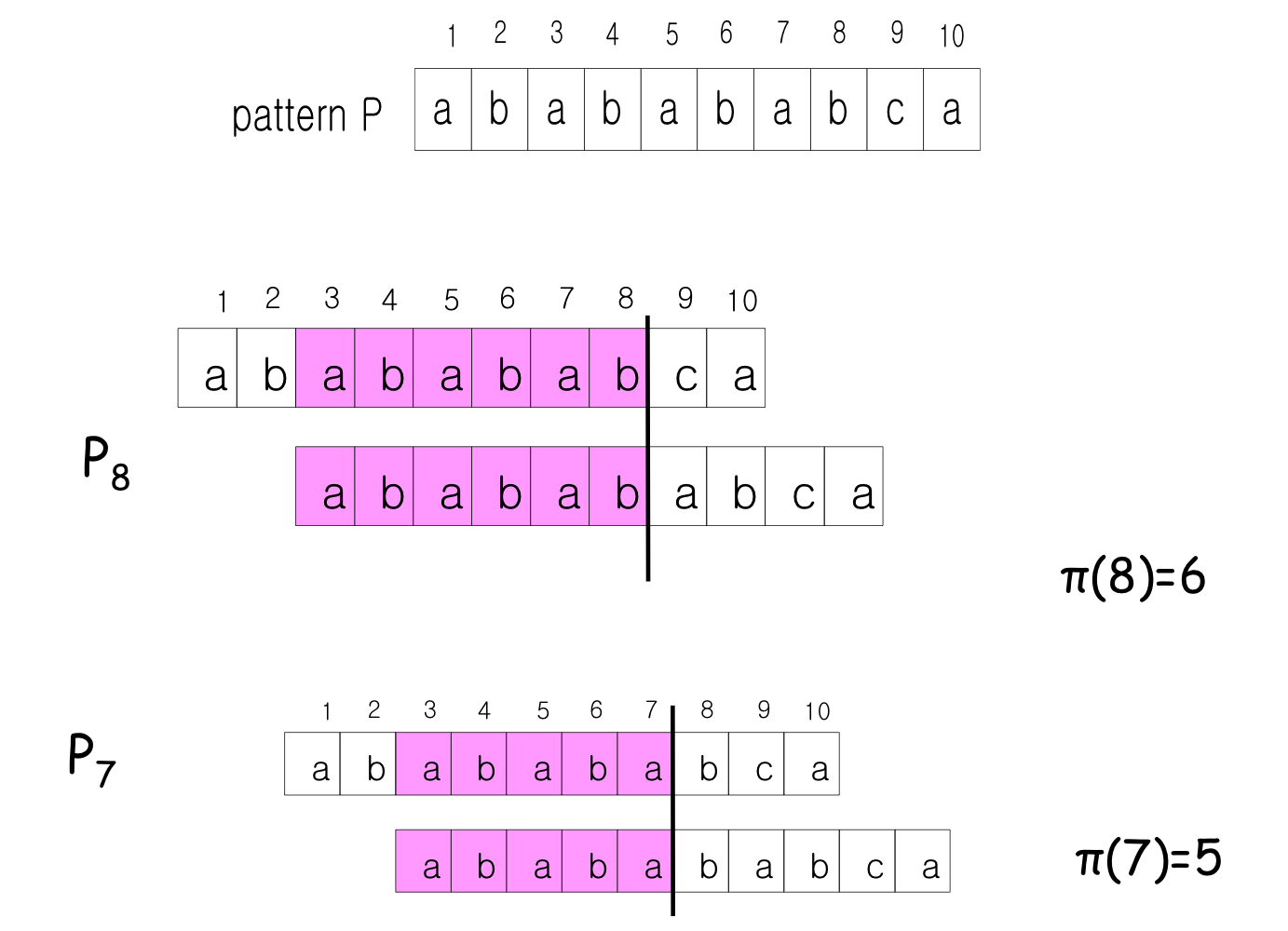
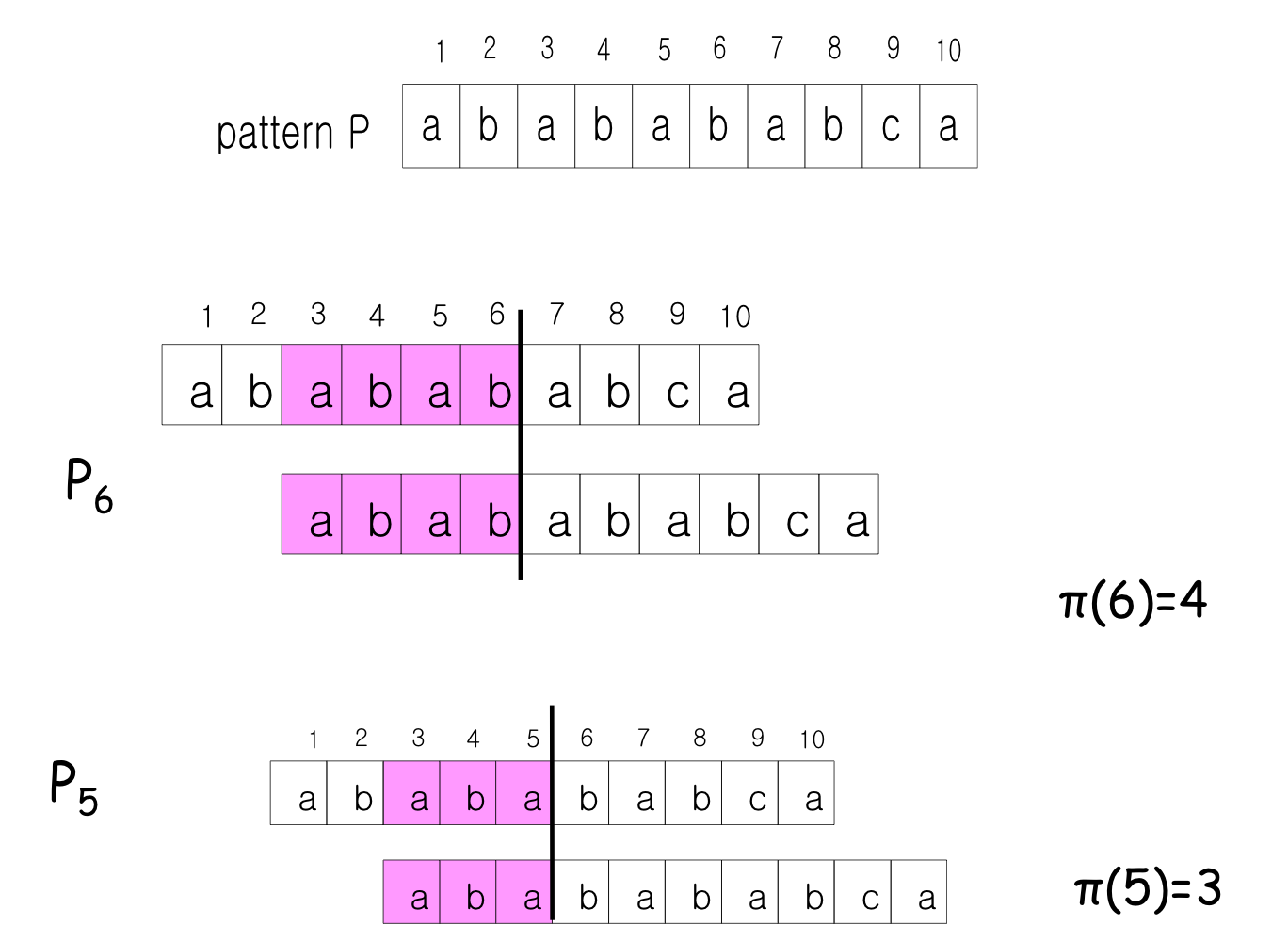
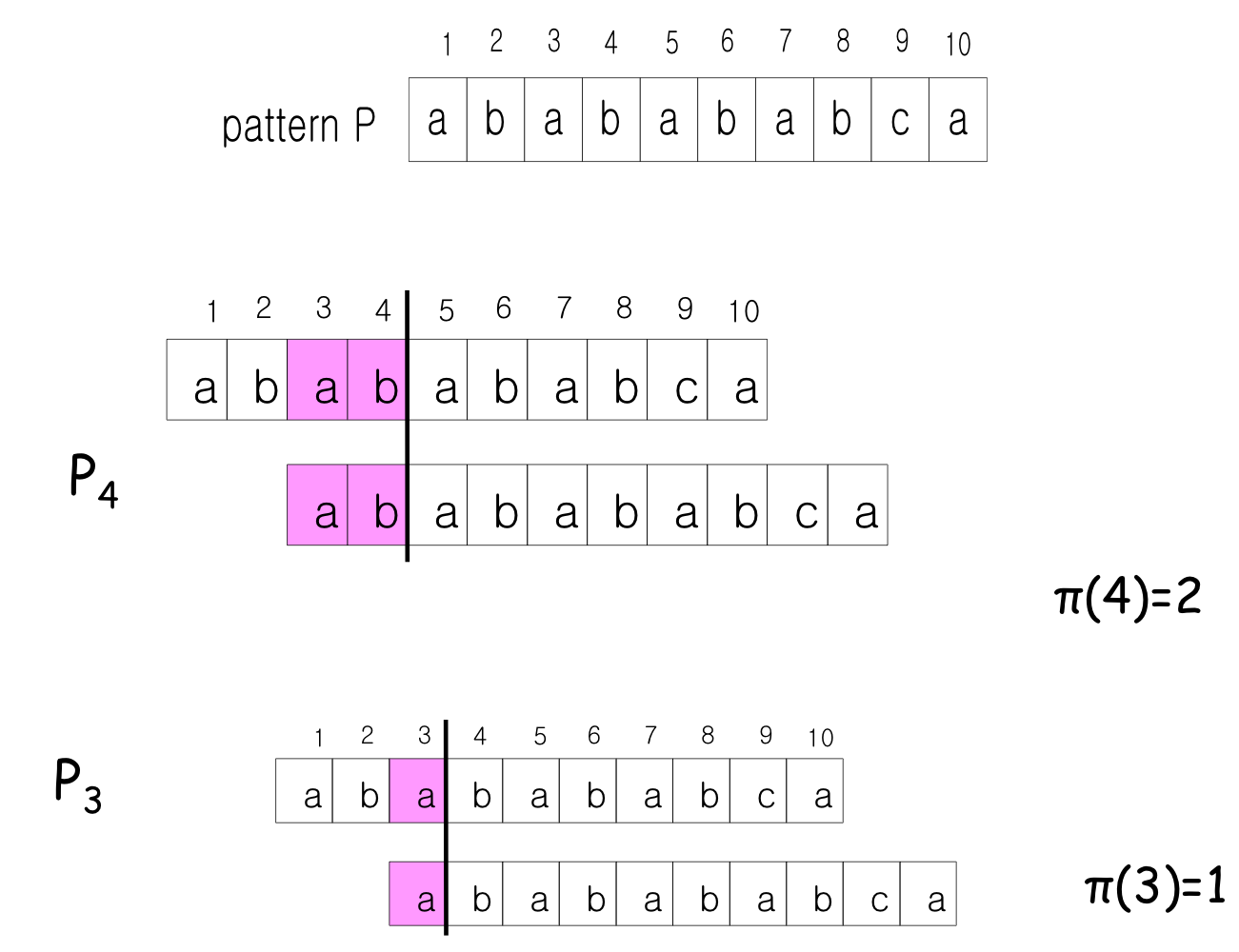
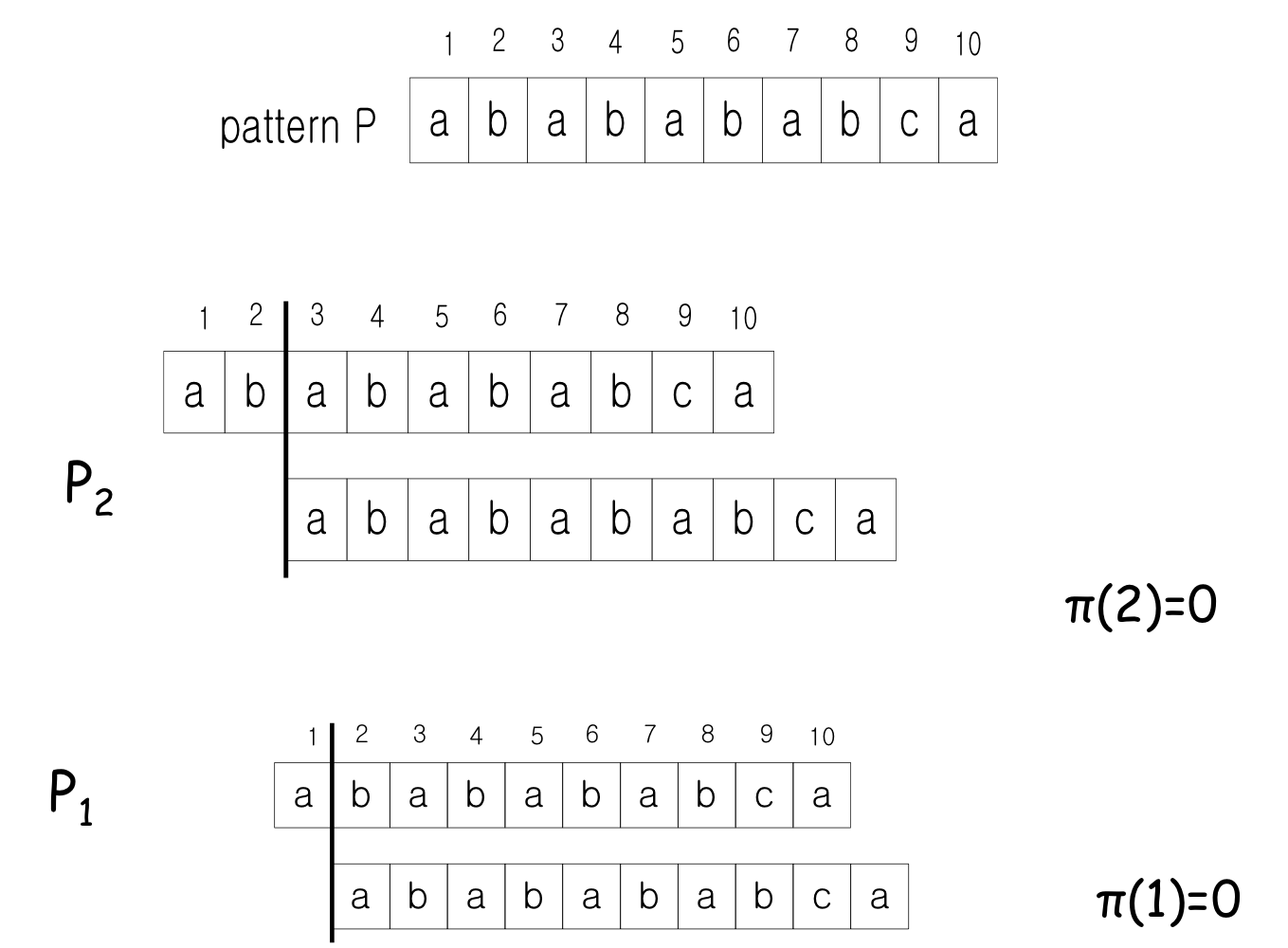
Prefix function $\Pi$

Example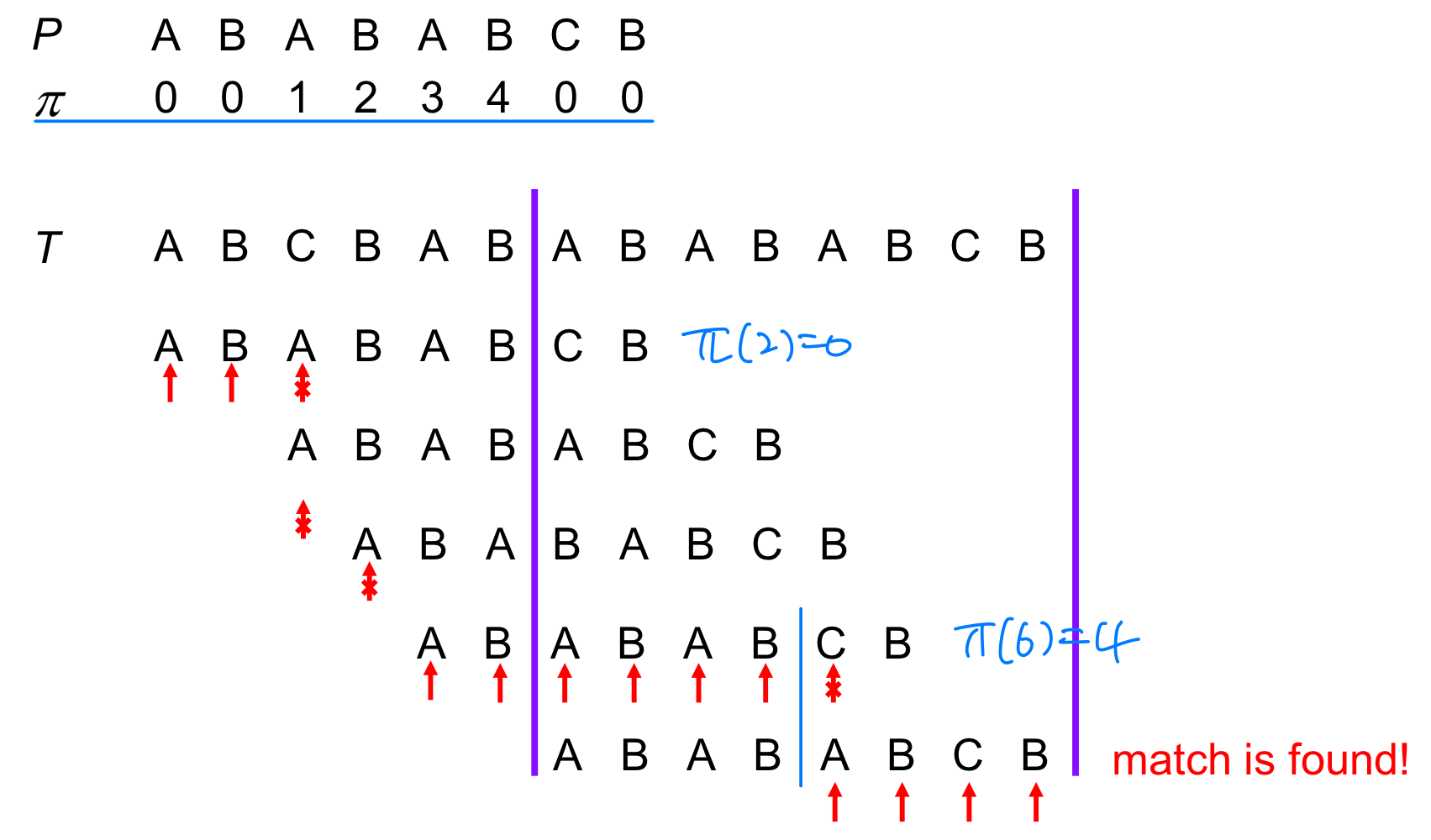

Case1

First character of the pattern does not match character of the text. (P[1] ≠ T[i])
➔ Shift pattern by 1
     == increment text index by 1
           (no change of pattern index)

Case2

Character (other than first) of the pattern does not match character of the text. (P[q+1] ≠ T[i])
➔ Shift pattern by value $\Pi$ value
(Prefix of P has already been compared)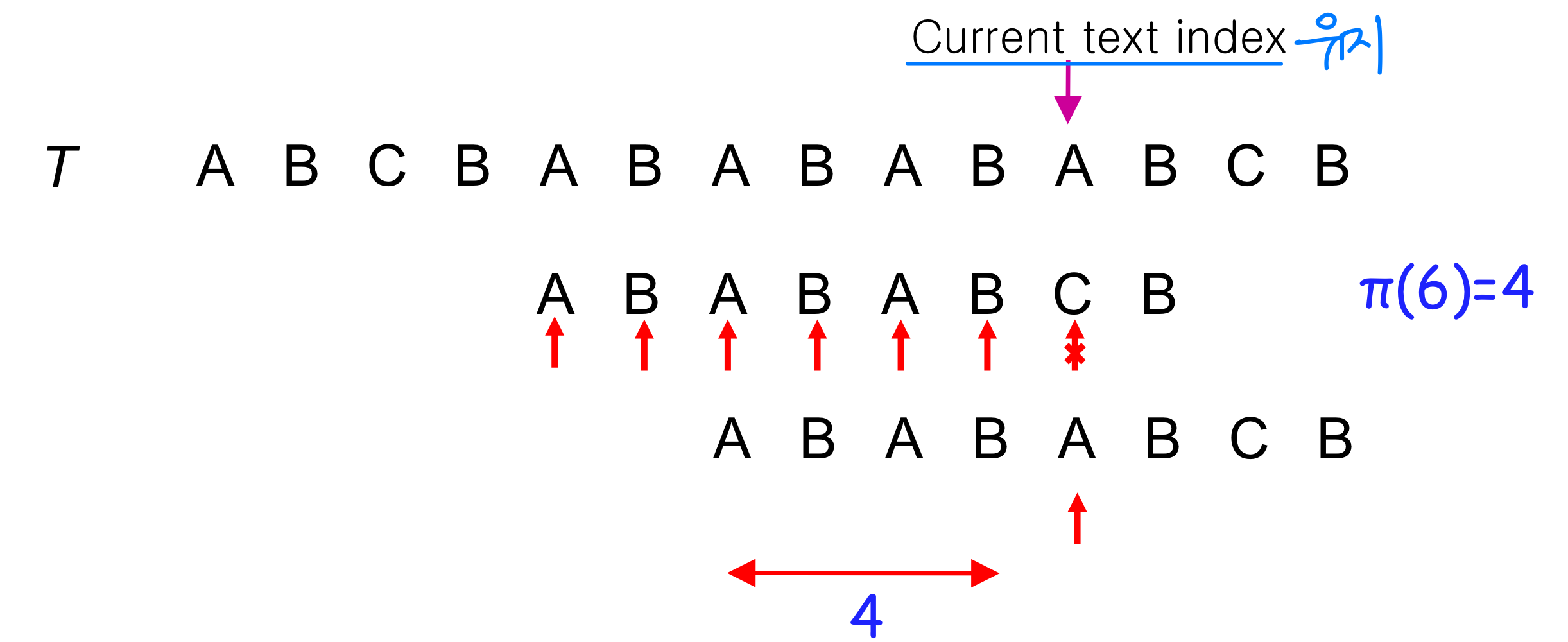

Case3

Character of the pattern matches character of the text. (P[q+1] = T[i])
➔ Increment text index and pattern index by 1And if all patterns are matched
➔ match is found

Algorithm

Example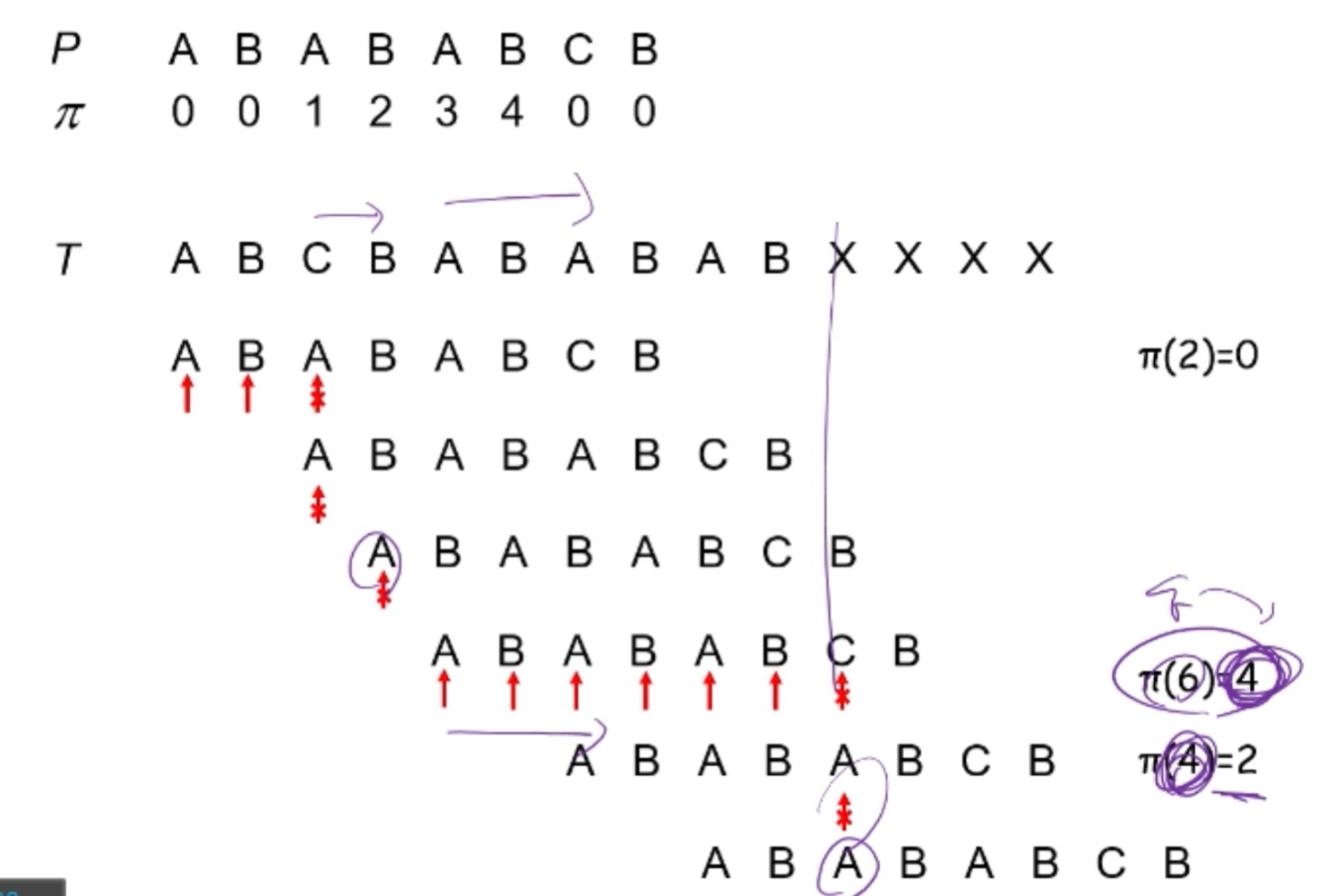

Running-time

• Using the amortized analysis (Sec 17.3)
  COMPUTE-PREFIX-FUNCTION : Θ(m)
  KMP-MATCHER : Θ(n)

Exercise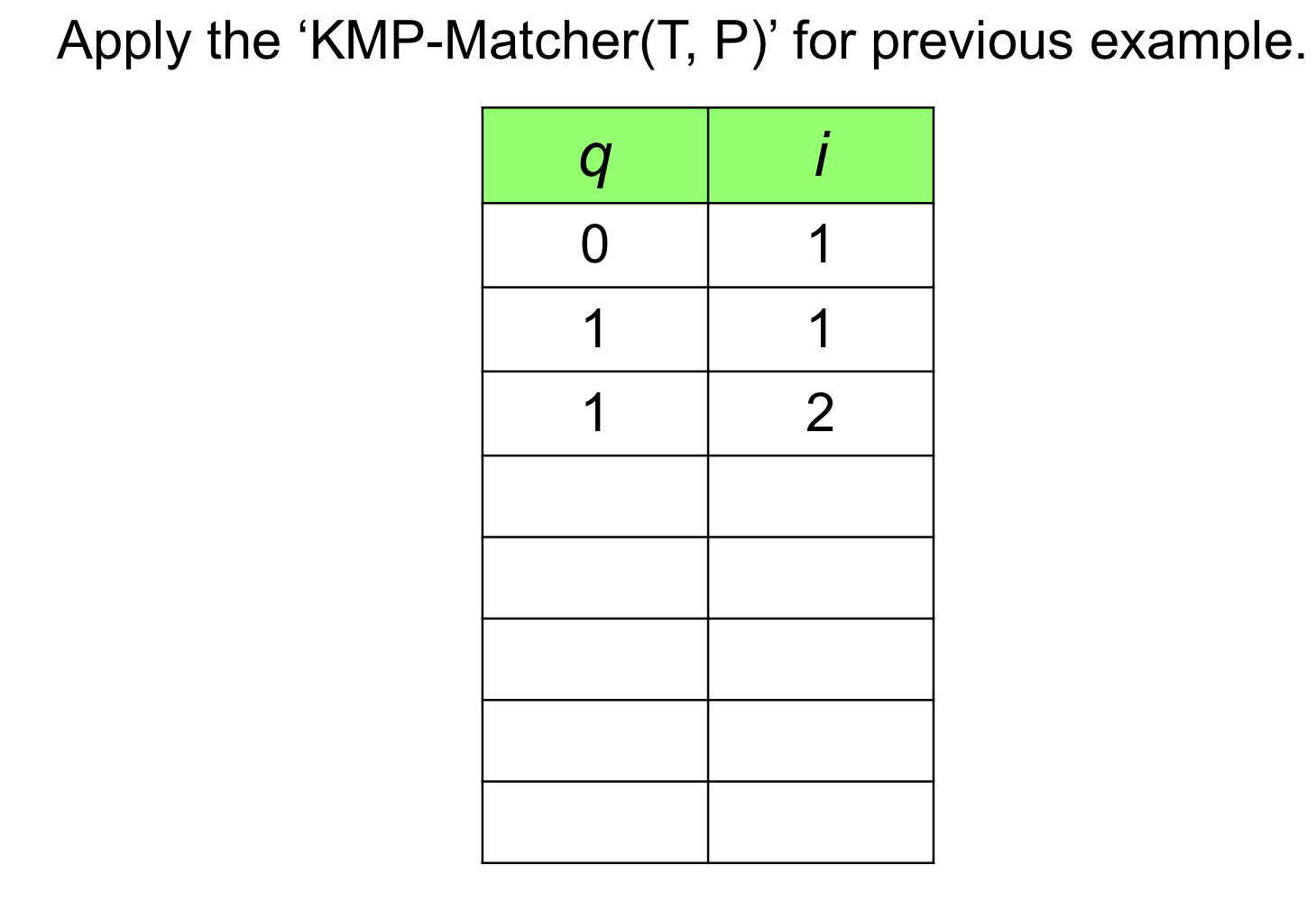

---

Exercise in Class

1. How many spurious hits does the Rabin-karp matcher (modulo q = 11)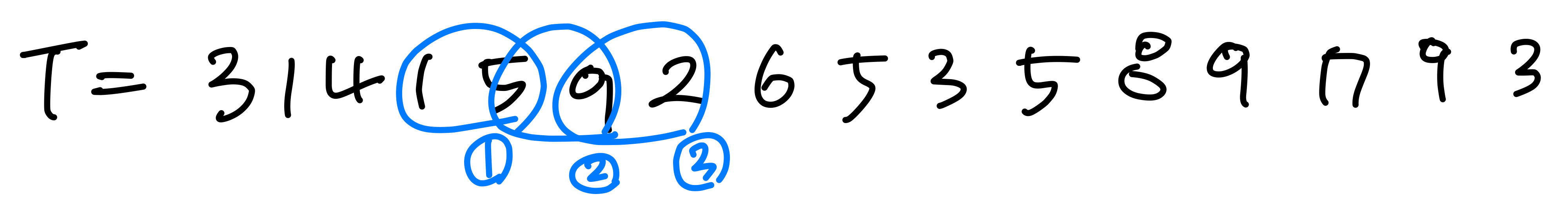When looking for the pattern p = 26?

→ 26 % 11 = 4, %11 = 4인 결과는 4개 그 중 3개가 spurious hits

2. Compute the prefix function $\Pi$ for the pattern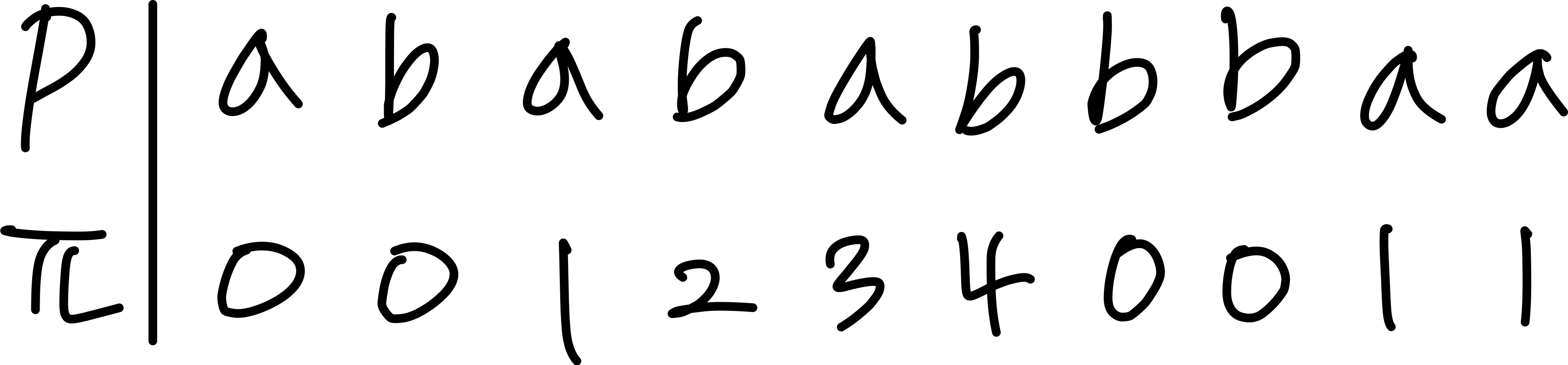

3. Run the KMP

HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.