- merge sort ➔ faster
- insertion sort ➔ sort in place
- Only constant # of array elements out side input array
- Heap sort ➔ both
Heap
: nearly complete binary tree implement as array
max tree : no smaller than its child
min tree : no larter than its child
max-heap : nearly complete BT + max tree
min-heap : nearly complete BT + min tree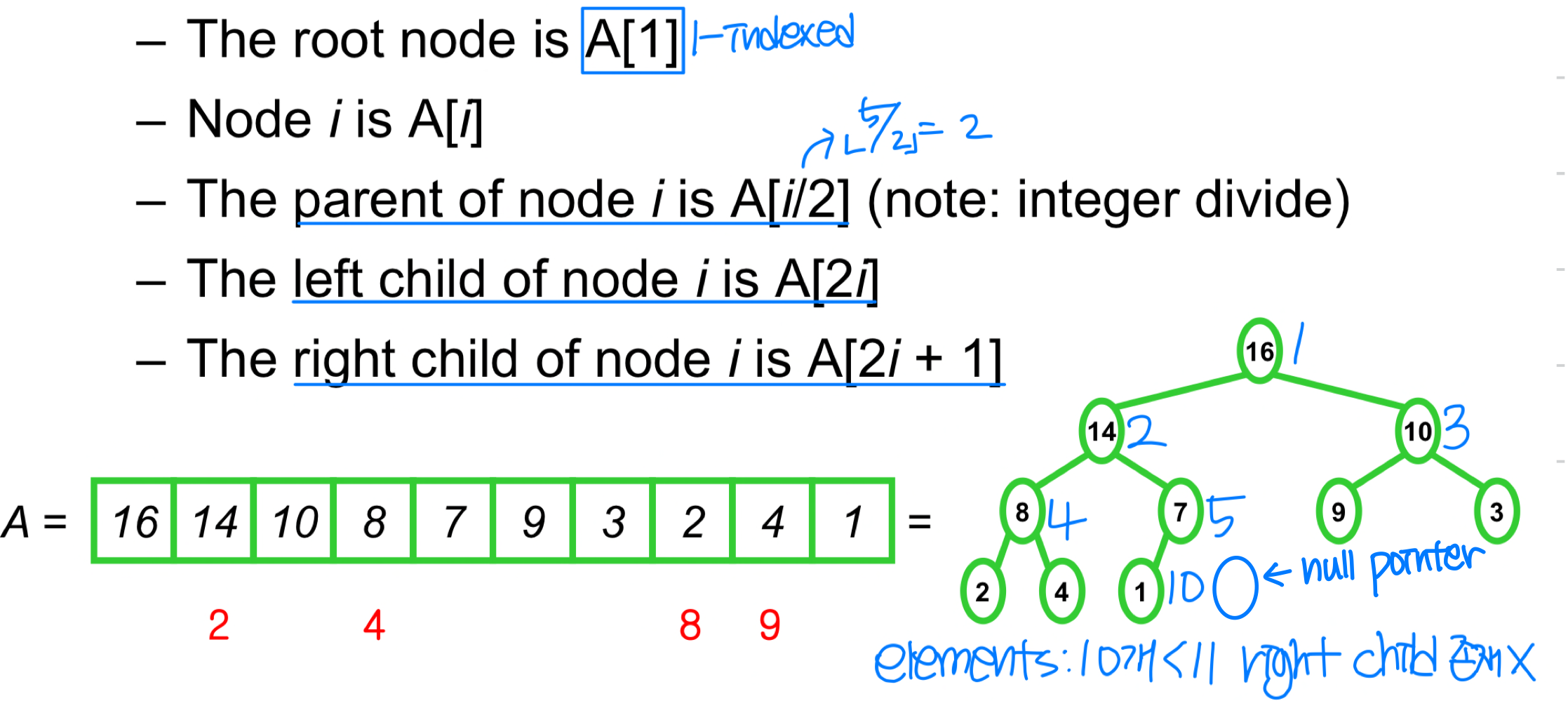
Heap Property
A[Parent(i)] >= A[i] for all nodes i > 1
- In other words, the value of a node is at most the value of its parent
- Where is the largest element in a heap stored? root
- The height of a node in the tree = the number ofedges on the longest downward path to a leaf
- The height of a tree = the height of its root = Θ(lg n) ➡️ n : element #
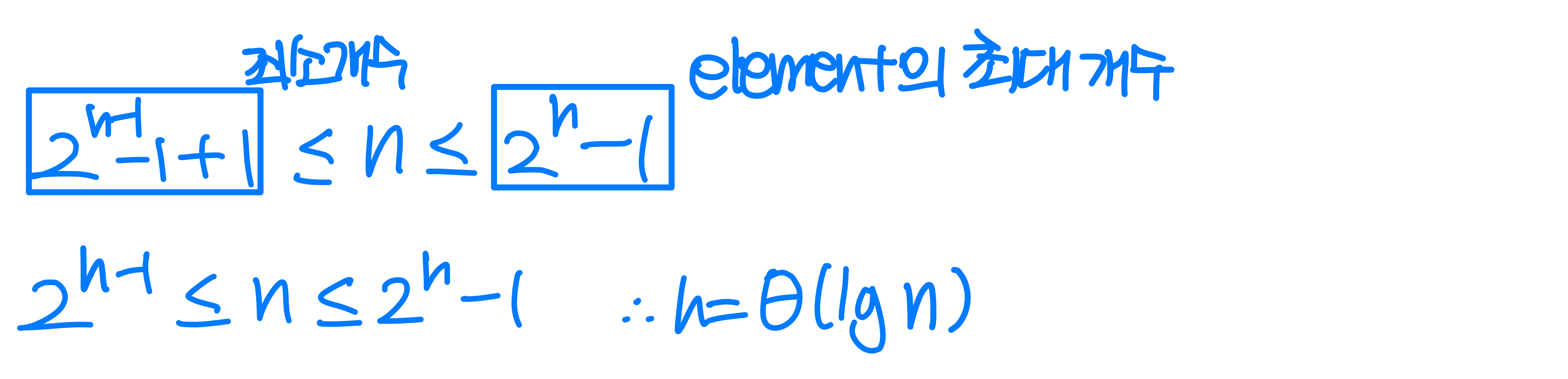
Max-heapify
: maintains the max-heap property
- Before MAX-HEAPIFY, A[i] may be smaller than its children.
- Assume left and right subtrees of i are max-heaps
- After MAX-HEAPIFY, subtree rooted at i is a max- heap
➡️ A[i] “float down", so subtree rooted at i becomes max-heap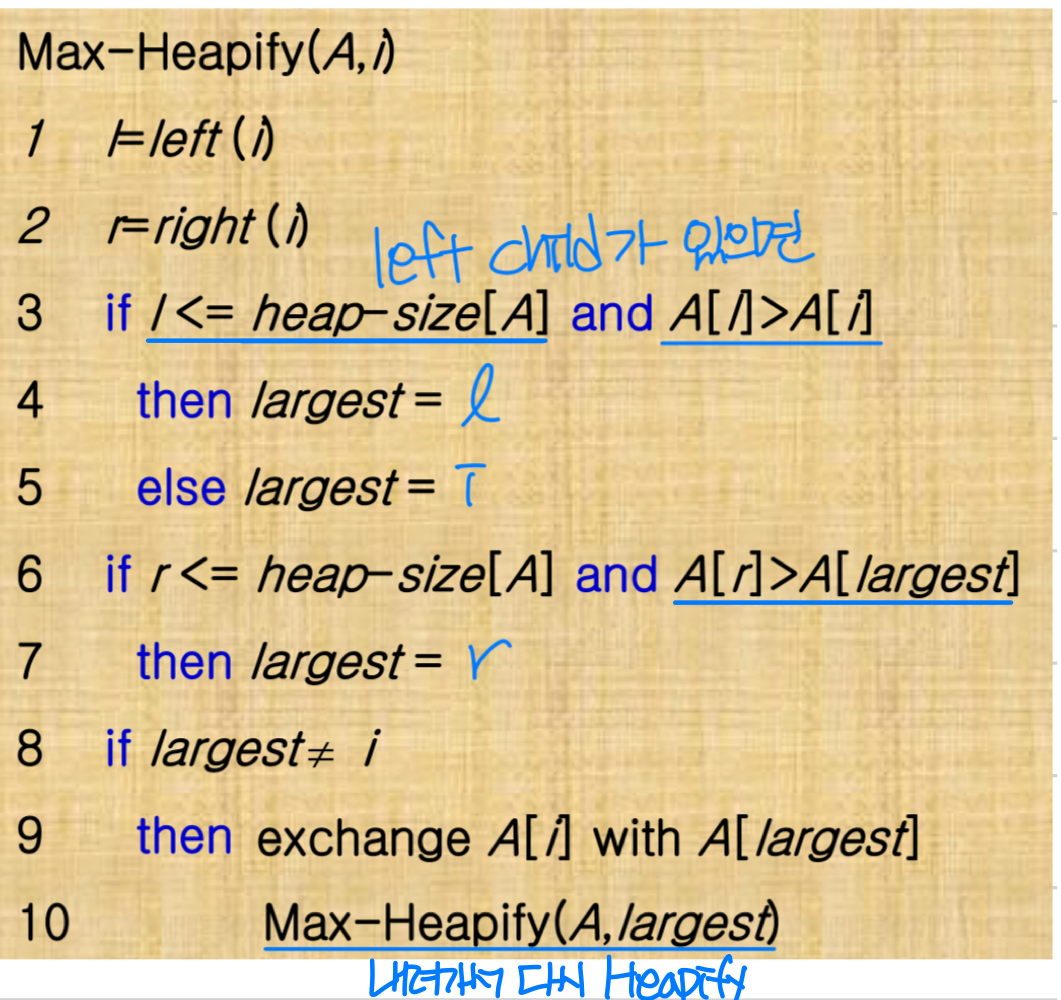
Analyzing Heapify
- Fixing up relationships(비교, assign) between i, l, and r takes Θ(1) time
- Worst case = Most unbalanced case ( 왼쪽만 full )
- 2n/3 on left subtree and n/3 on right subtree (bottom row 1/2 full) - So time taken by Max-Heapify() is given by T(n) <= T(2n/3) + Θ(1)
By case 2 of the Master Theorem, T(n) = O(lg n)
Build-max-heap
: in bottom-up manner by running MAX-HEAPIFY on succesive(연속하는) subarrays
➡️ length nA[n/2 + 1] ~ A[n] are heaps, why? child가 없는 노드
So, from n/2 to 1, calling Max-Heapify() on each node
Analyzing Build-max-heap
- Each call to Max-Heapify() takes O(lg n) time
- There are O(n) such calls (specifically, n/2)
- Thus the running time is O(n lg n)
➡️ Tighter bound : O(n)
Heapsort
- phase1 : Arb.arr ➡️ Heap
- phase2 : Sorting

Priority Queues
- Maintains a dynamic set S of elements
- Dynamic Set : The set that can grow(증가), shrink(감소), or otherwise change over time
- Each set element has a key
- Example of max-priority queue : schedule jobs on shared computers
- Example of min-priority queue : Utilizing the service machine time. Job with smallest is selected
Example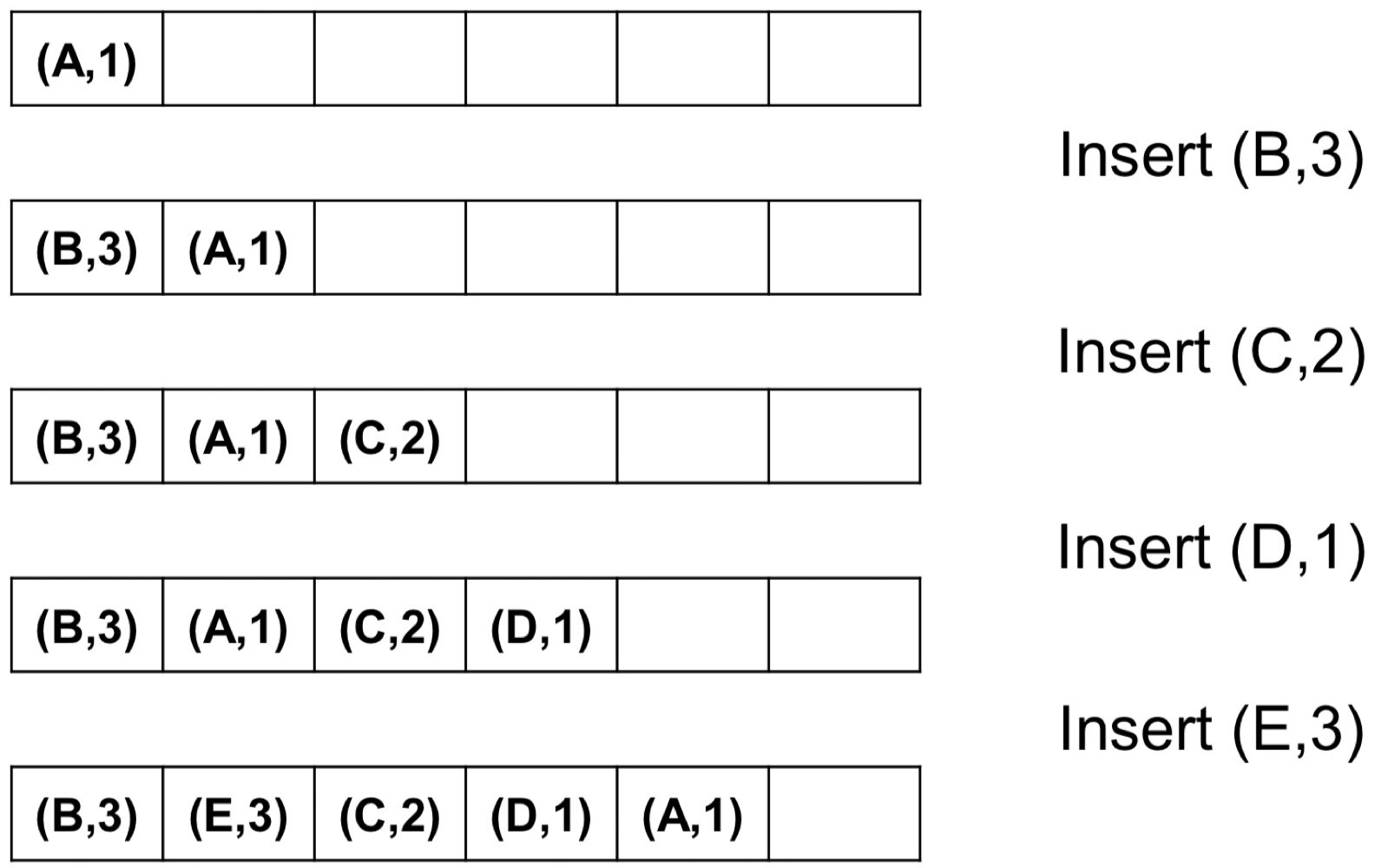
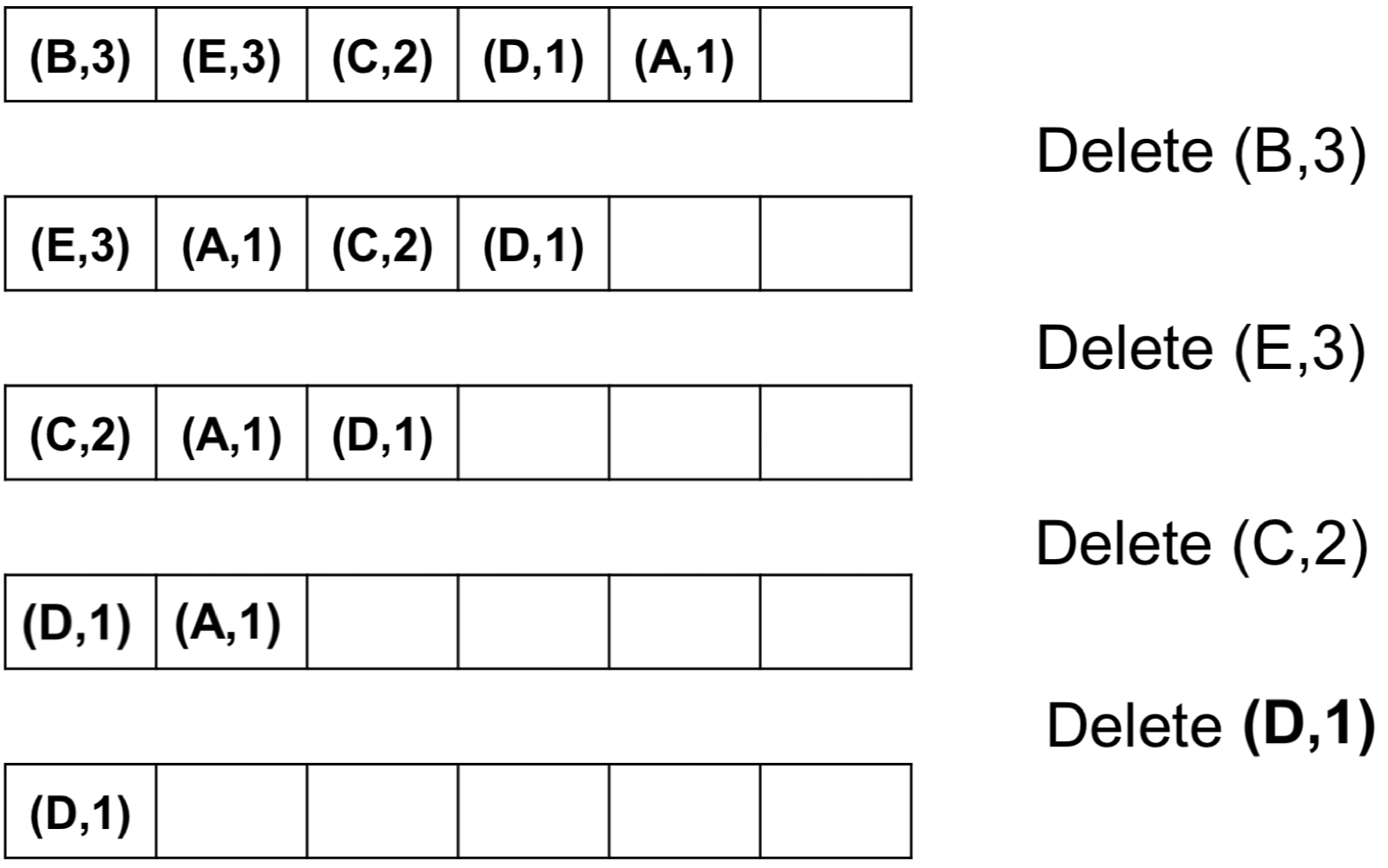
Operations
Insert(S, x) ; inserts element x into set S
MAXIMUM(S) : returns element of S with largest key
EXTRACT-MAX(S) : removes and returns element of S with largest key
INCREASE-KEY(S, x, k) : increases value of element x’s key to k
Exercise in class
1. Priority queue using heap은 들어오는 순서와 상관없이 only 우선순위?
➡️ No, 순서에 따라 바뀌기 때문에 순서도 의미가 있다.
2. Max-heap or not?
(1) | 100 | --- | 89 | 67 | 25 | 80 | --- | --- | ➡️ No
(2) | 100 | 90 | 52 | 89 | 67 | 25 | 55 | 80 | ➡️ No
(3) | 100 | 40 | 82 | 35 | 25 | 1 | --- | --- | ➡️ Yes
3. T / F
(1) An array that is sorted in ascending order is a min-heap ➡️ T
(2) The smallest element in max-heap is the last element in array ➡️ F
4. Build-max-heap(A)
| 20 | 1 | 16 | 9 | 10 | 6 | 8 | 9 | 3 | 2 |
➡️ | 20 | 10 | 16 | 9 | 2 | 6 | 8 | 9 | 3 | 1 |
➡️ Tie breaking ( equal sign의 여부 )
5. Max-priority queue, what is final result?
- Insert(A, 4)
- Insert(B, 3)
- Insert(C, 5)
- Insert(D, 4)
- Delete
- Delete
- Insert(E, 4)
- Insert(F, 5)
- Delete
➡️ | A, 4 | B, 3 | E, 4 |
HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.

