- Proposed by C. A. R. Hoare in 1962
- Divide-and-conquer algorithm
- Sorts in place
- Very practical(실용적) ( with tuning(selecting pivot) )
Divide-and-Conquer
- Quicksort an n - element array:
1. Divide: Partition the array into two subarrays around a pivot x such that elements in lower subarray ≤ x ≤ elements in upper subarray → 가장 중요 2. Conquer: Recursively sort the two subarrays
2. Conquer: Recursively sort the two subarrays
3. Combine: Trivial
Key: Linear- time partitioning(divide) subroutine
Partitioning subroutine
Exercise
Illustrate the operation of “PARTITION()” on the array of A = {2, 8, 7, 1, 3, 5, 6, 4}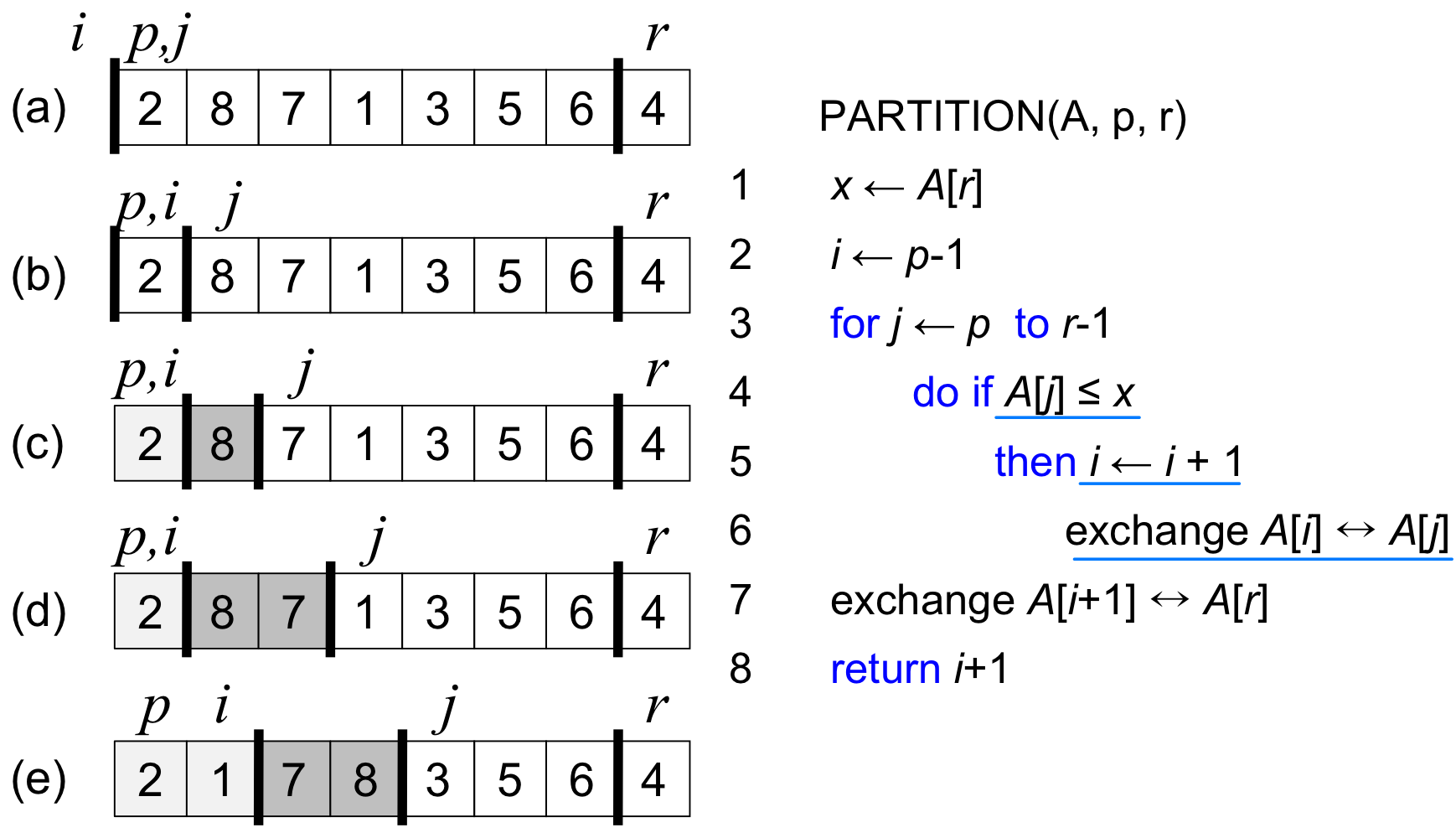

Algorithm
Correctness
- Loop invariant :
- All entries in A[p..i] are ≤ pivot
- All entries in A[i+1 .. j-1] are > pivot
- A[r] = pivot
- Initialization : True, because A[p..i], A[i+1..j-1] are empty. (Prior to the first iteration of the loop, i=p-1, and j=p)
- Maintenance : While the loop is running, if A[j] ≤ pivot, then A[j] and A[i+1] are swapped and then i and j are incremented. If A[j] > pivot, then increment only j.
- Termination : When the loop terminates, j = r, so elements in A are partitioned into one of the three cases.
- Running time : Ө(n)
Worst-case
- When the partitioning routine produces one subproblem with n-1 elements and one with 0 element.
- input is sorted in ascending or descending case of quicksort order → pivot is largest or smallest case
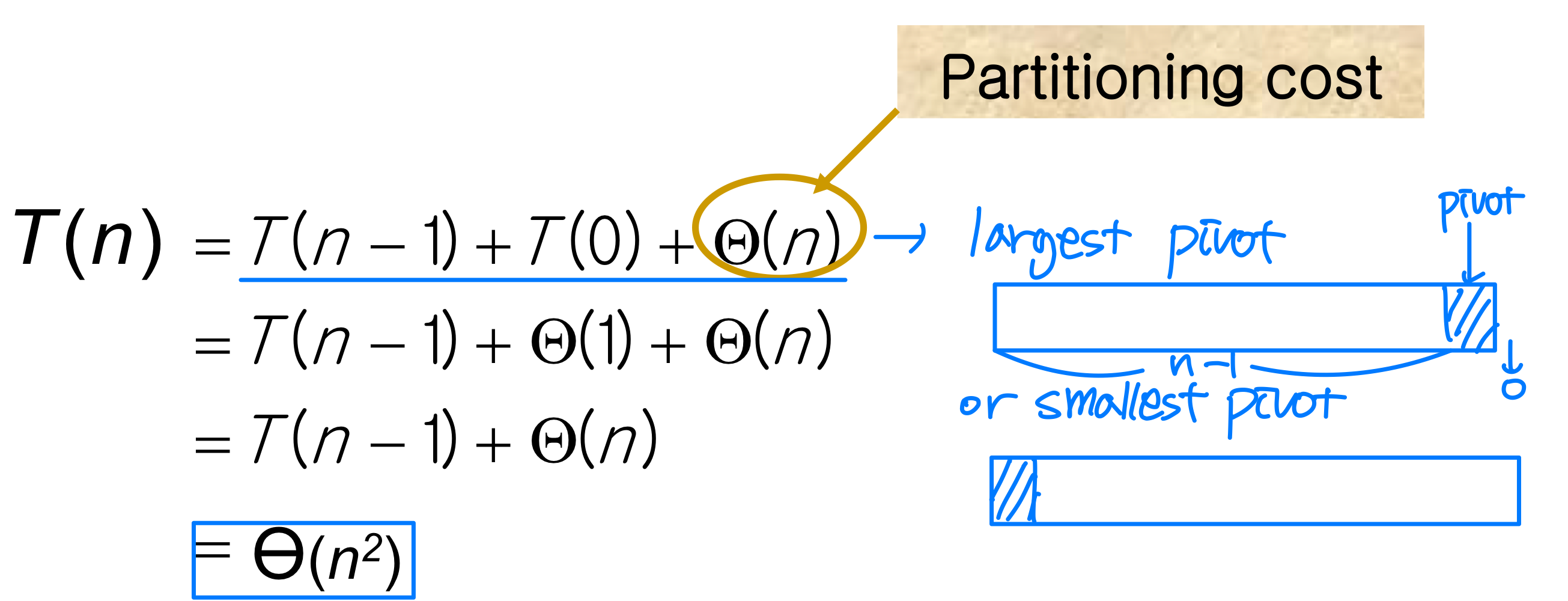
- input is sorted in ascending or descending case of quicksort order → pivot is largest or smallest case
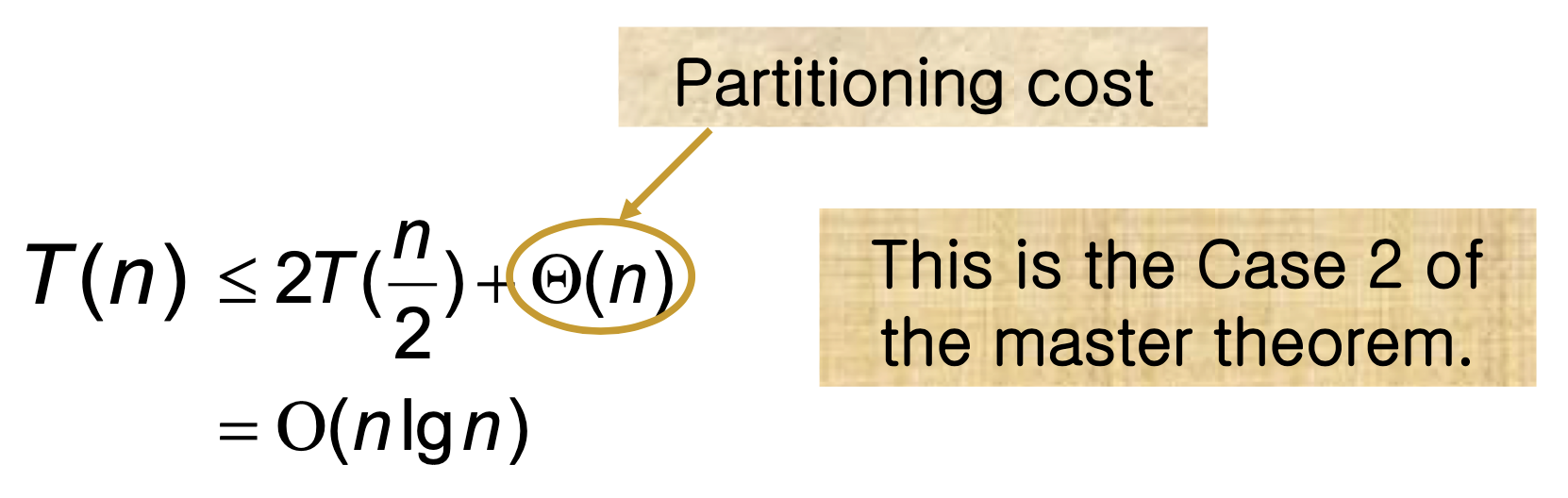
Best-case
- When the partitioning routine produces two subproblems, each of size no more than n/2.
Average-case
- Average-case running time of quicksort is much closer to best case than to the worst case.
- Book discusses two solutions for average-case analysis:
- Randomize the input array – Intuitive(직관적) analysis
- Randomized version of quicksort (Pick a random pivot element) – formal analysis
Intuition : Balanced(?) partitioning
- First, a more intuitive explanation/example:
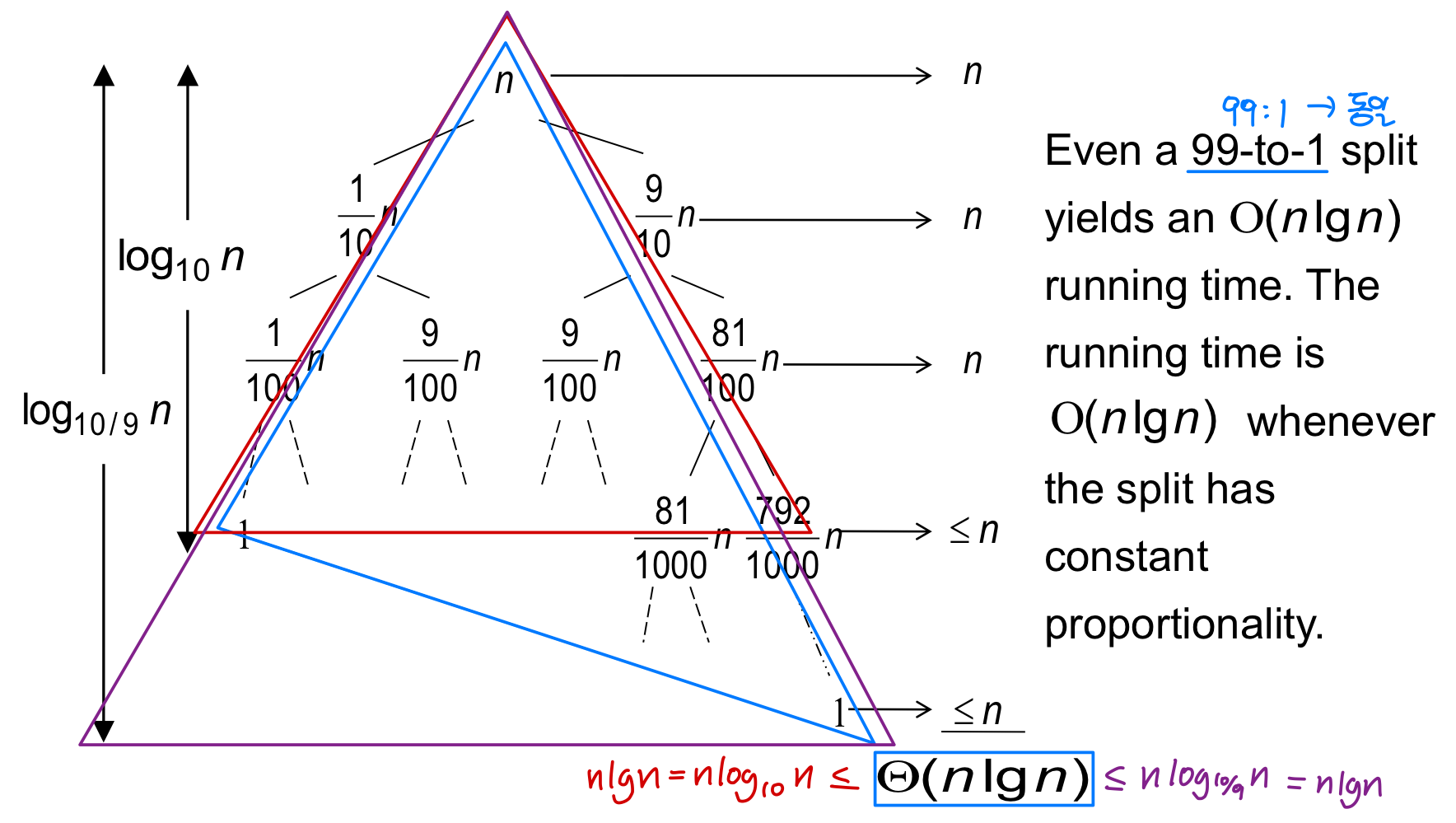
- Suppose that partition() always produces a 9-to-1( 9 : 1 ) split. This looks quite unbalanced!
- The recurrence is thus:
T(n) = T(9n/10) + T(n/10) + cn - How deep will the recursion go? (draw it)
Intuition for the average case
- Intuitively, a real-life run of quicksort will produce a mix of “bad” and “good” splits
- Randomly distributed among the recursion tree
- Pretend for intuition that they alternate between best-case [(n-1)/2 : (n-1)/2] and worst-case [n-1 : 0]
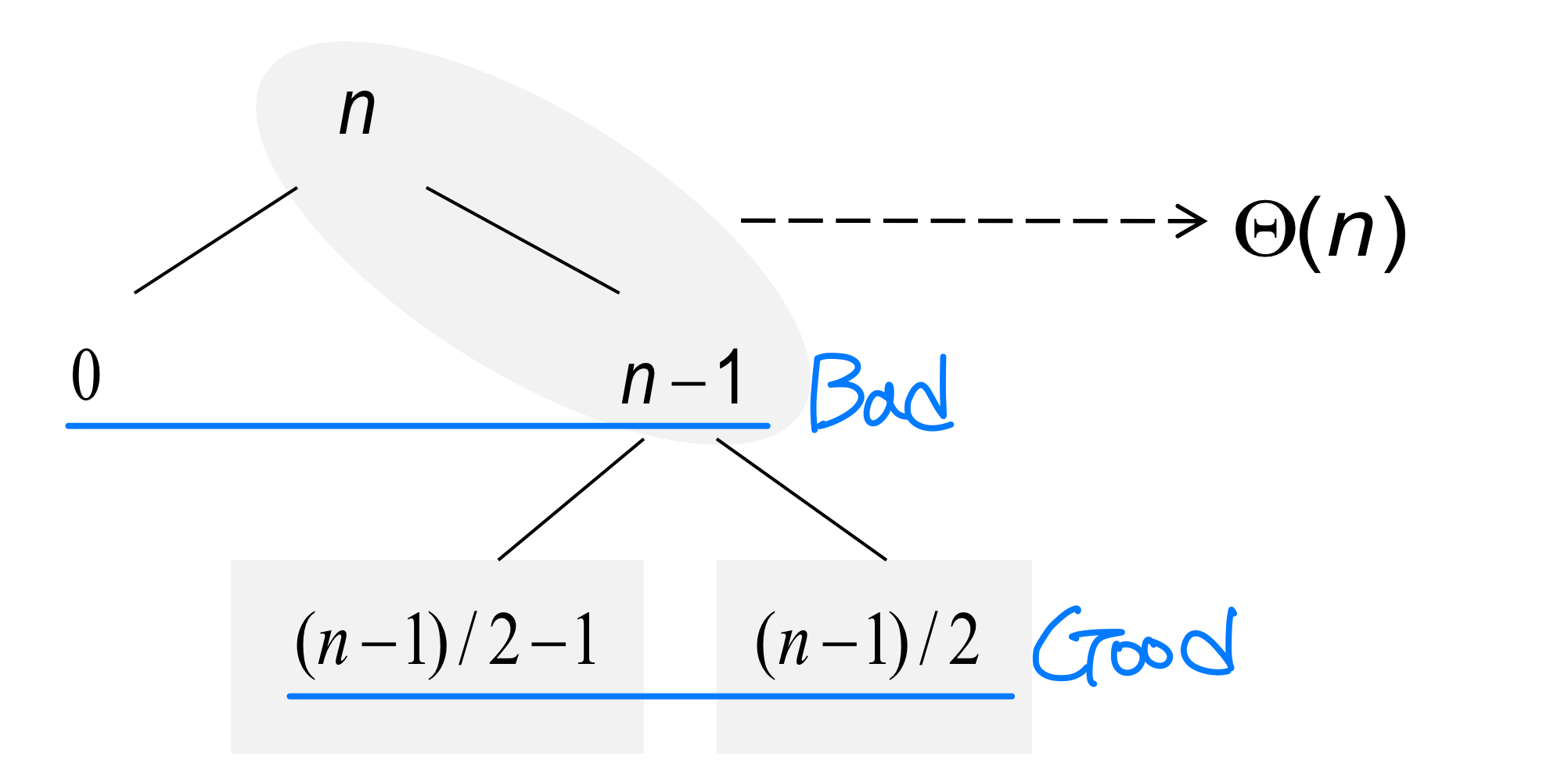
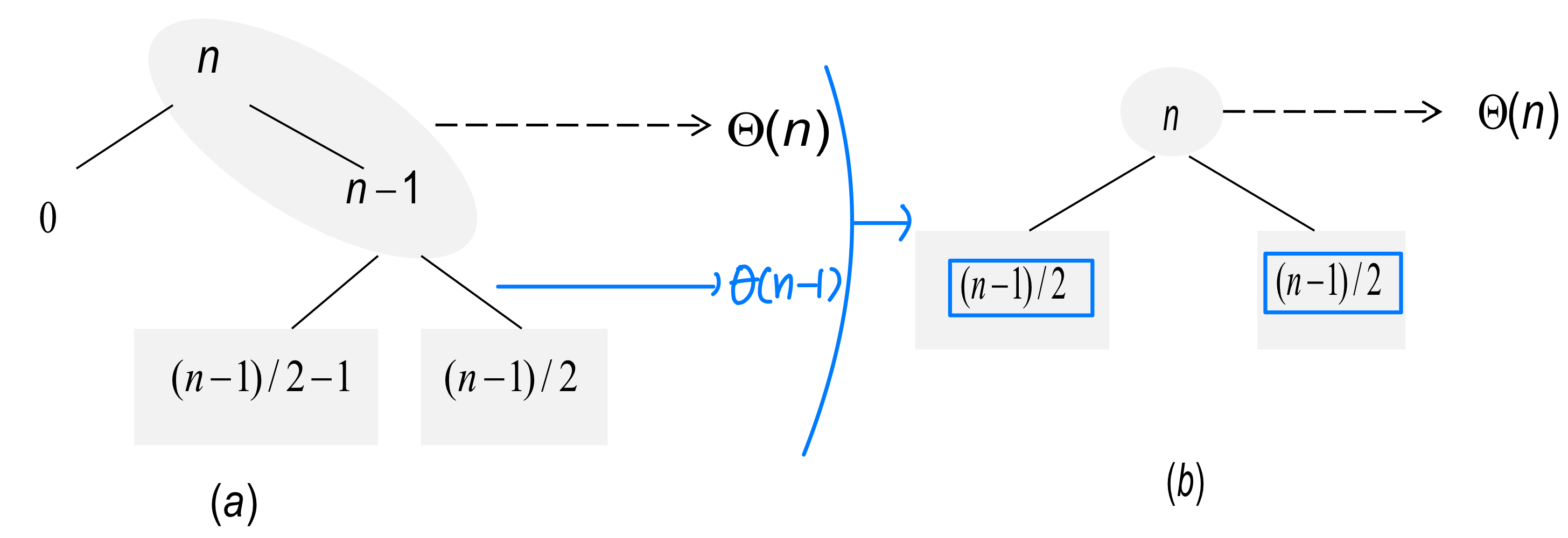
- What happens if we bad-split root node, then good- split the resulting size (n-1) node?
- We end up with three subarrays, size 0, (n-1)/2 -1, and (n-1)/2
- Combined cost of splits = Ө(n) + Ө(n -1) = Ө(n)
- No worse than if we had good-split alone! → good split만 했을때와 동일

Formal : Randomization
- If input array A is almost or already sorted, choosing the last element as a pivot yields a poor performance.
- Instead, choose a random element as a pivot!
- Randomization of quicksort stops any specific type of array from causing worst-case behavior
Analyzing Quicksort: Average Case
- For simplicity, assume:
- All inputs are distinct ( no repeats(duplicate) )
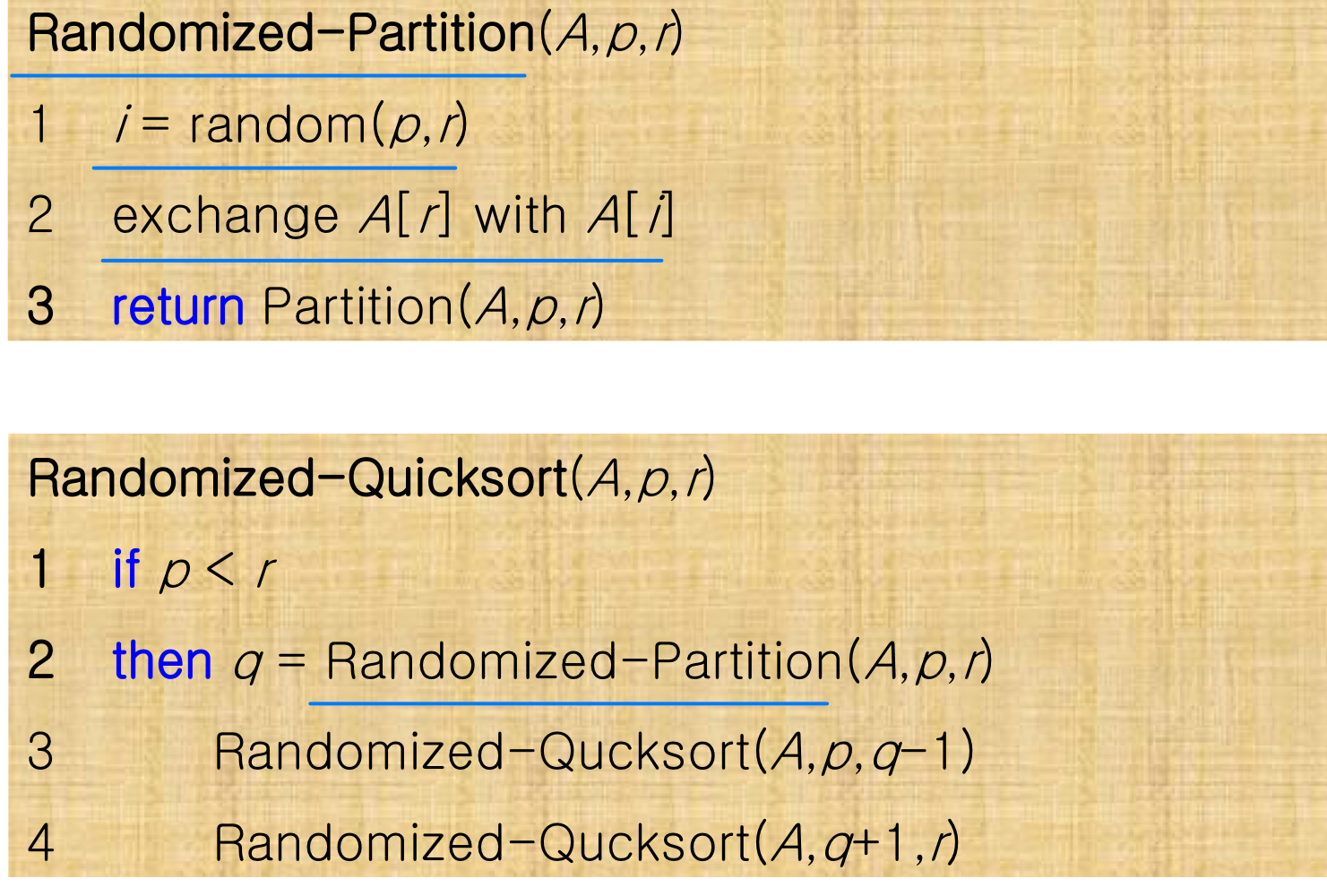
- Randomized-partition() procedure
- partition around a random element from the subarray.
- all splits (0:n-1, 1:n-2, 2:n-3, ... , n-1:0) are equally likely to happen. → 각각 1/n
- What is the probability of a particular split happening?
- Answer: 1/n
- So partition generates splits
(0:n-1, 1:n-2, 2:n-3, ... , n-2:1, n-1:0)
each with probability 1/n - If T(n) is the expected running time,
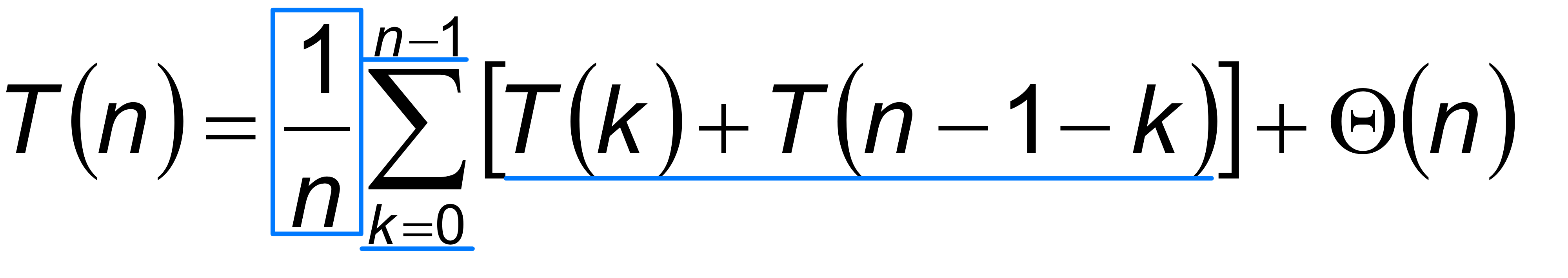
- What is each term under the summation for? → k=0, 0 : n-1 ... k=n-1, n-1 : 0
- What is the Ө(n) term for? → partition cost
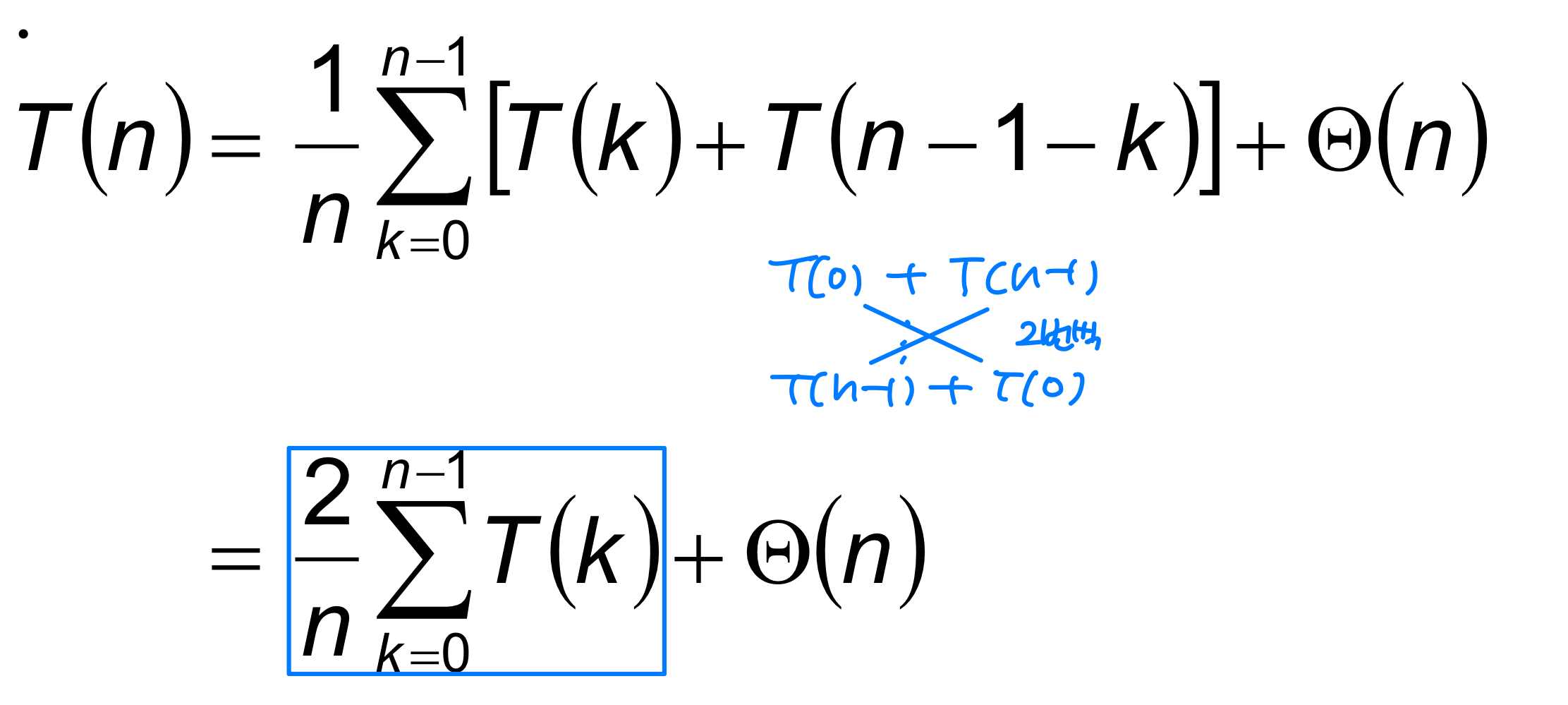
- We can solve this recurrence using the dreaded substitution method.
- Guess the answer
- T(n) = O(n lg n)
- Assume that the inductive hypothesis holds
- T(n) ≤ an lg n + b for some constants a and b
- Substitute it in for some value < n
- The value k in the recurrence
- Prove that it follows for n
- Grind through it...
- Guess the answer



- So T(n) ≤ an lg n + b for certain a and b – Thus the induction holds
– Thus T(n) = O(n lg n)
– Thus quicksort runs in O(n lg n) (→ Ө(n lg n) ) time on average
(phew!) - Oh yeah, the summation...
The Key Summation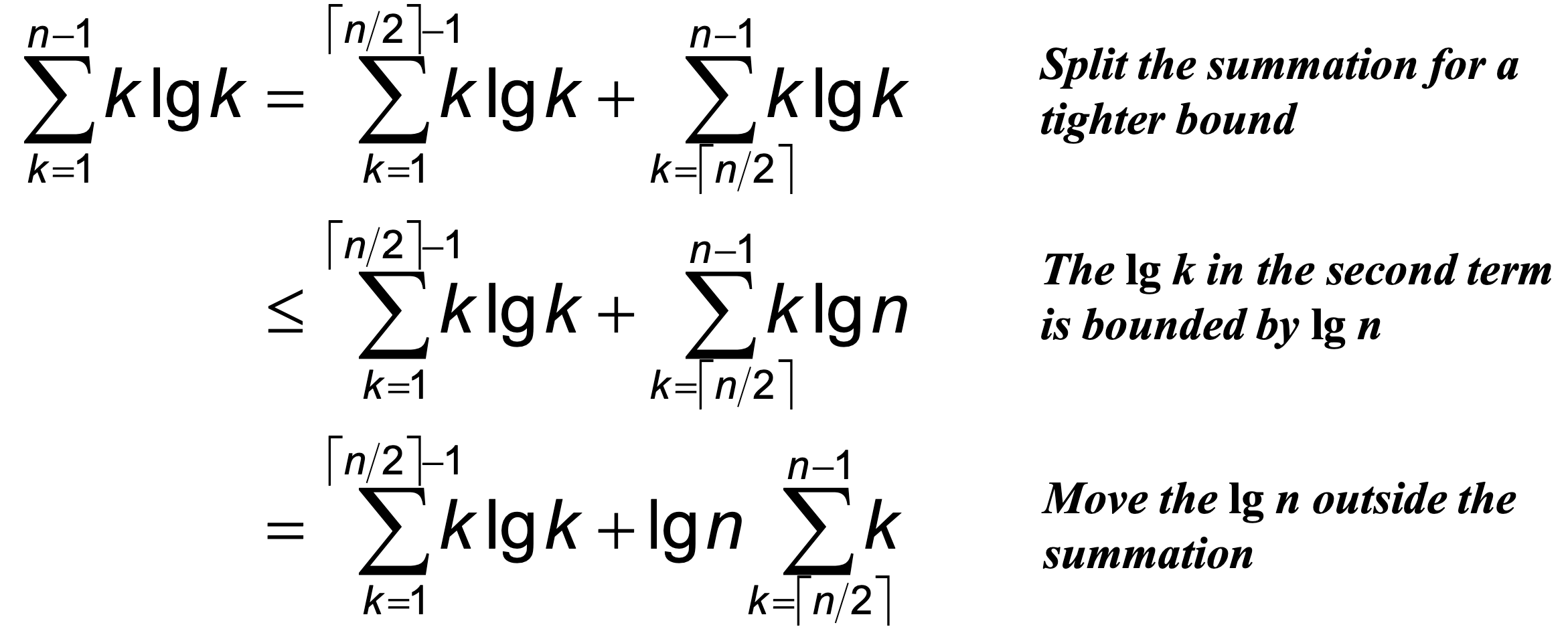


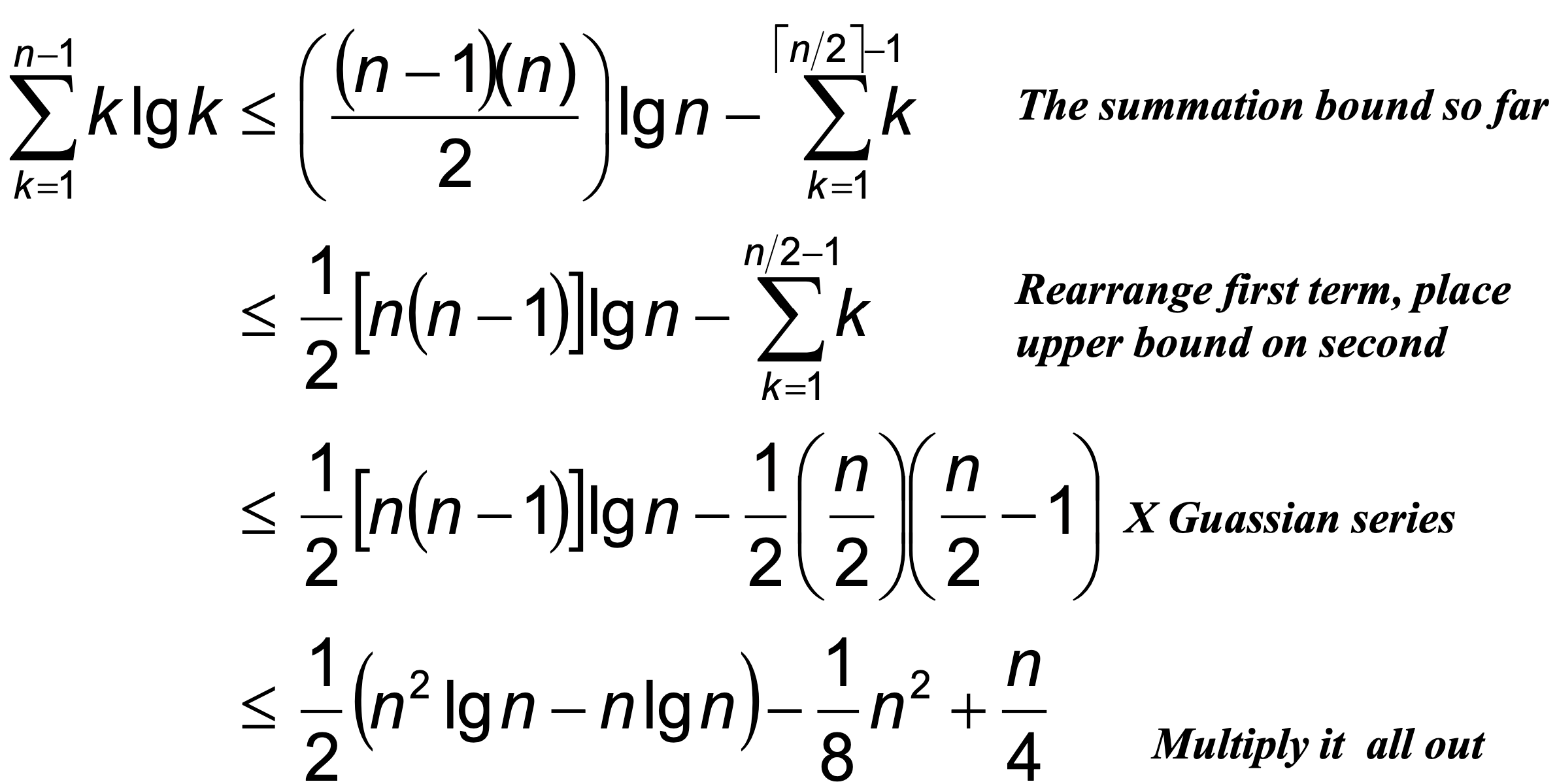
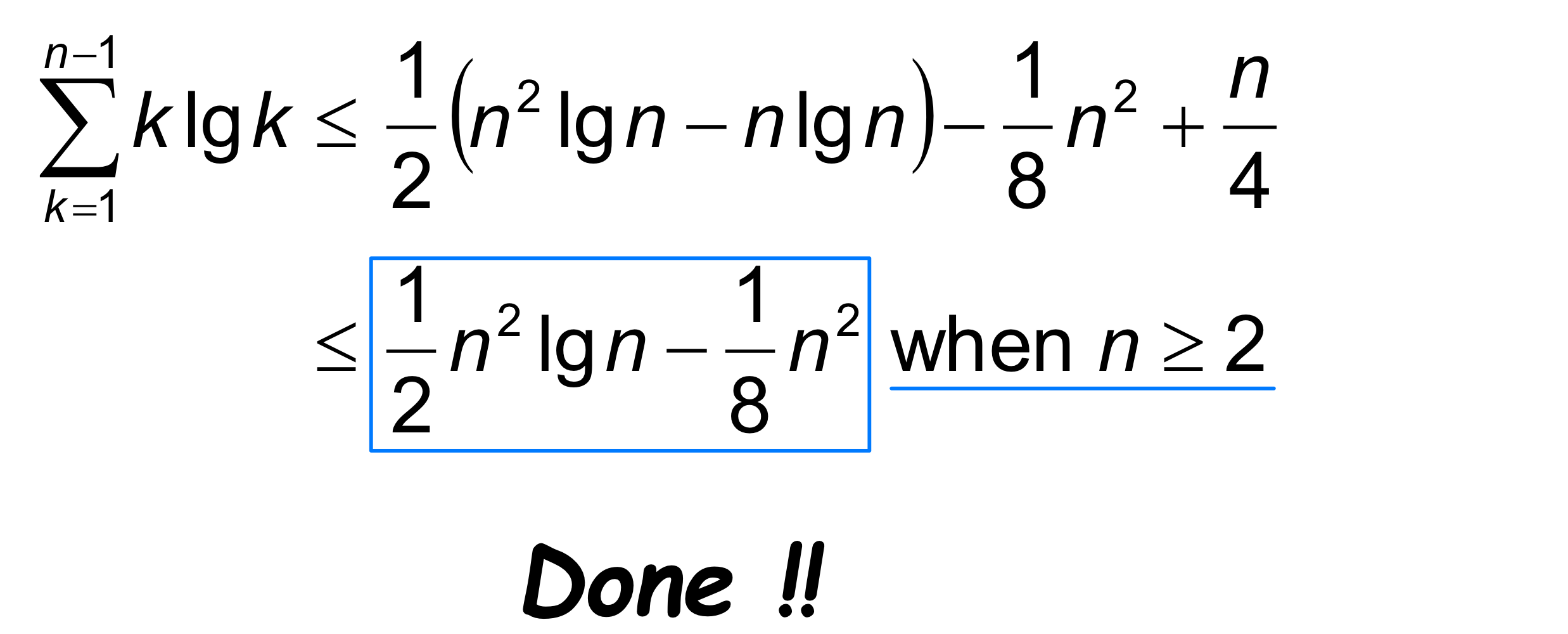
Exercise in Class
1. Running time
Worst case : Ө(n)
Best case : Ө(n lgn)
Average case : Ө(n lgn)
2. Express the time complexity T(n) as a recurrence equation
Worst case : T(n-1) + T(0) + Ө(n) = T(n-1) + Ө(n)
Best case : 2T(n/2) + Ө(n)
Average case : in Slide 방법 3가지
HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.

