[ DB ] 02. Relational Algebra

🖥️ Relational algebra

• Algebra
  • Mathematical system consisting of
    - Operands: variables or values from which new values can be constructed
    - Operators: symbols denoting procedures that construct new values from given operands
• Relational Algebra
  • A procedural language consisting of a set of operations that take one or two relations as input and produce a new relation as their output

---

Select: σ

• The select operation selects tuples that satisfy a given predicate
• Notation: $σ_p(r)$
  ∧ (and), ∨ (or), ¬ (not)

Ex_

---

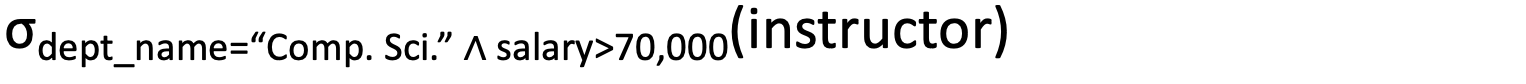
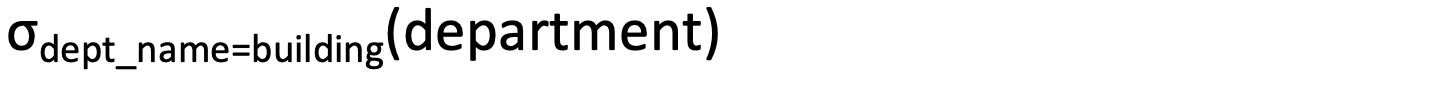
Project: ∏

• A unary operation that returns its argument relation, with certain attributes left out
• Notation:$∏_{A1,A2,A3,...,Ak}(r)$
  ➡️ Duplicate rows are removed
  

Ex_

---

Cartesian product: ×

• The Cartesian-product operation (denoted by ×) combines information from any two relations
• Binary operator (2 operands) ➡️ cf. σ, ∏ : unary operator(1 operand)

Ex_

---

Join: ⋈

• The join operation combines a select operation and a Cartesian- Product operation into a single operation
  $𝑟⋈_\theta𝑠 = σ_\theta(𝑟×𝑠)$

Ex_

---

Union: ∪

• The union operation combines two relations as a superset of both
• Notation: $r∪s$
• ⭐️ For $r∪s$ tobevalid,
  1. r, s must have the same number of attributes (same arity)
  2. The attribute domains must be compatible
  • E.g., the 2nd column of r deals with the same type of values as does the 2nd column of s

➡️ ⭐️ Duplicate remove

Ex_

---

Set-intersection: $\cap$

• The set-intersection operation finds tuples that are in both the input relations
• Notation: $r\cap s$
• Assumptions:
  • $r, s$ have the same arity
  • Attributes of r and s are compatible

Ex_

---

Set-difference: –

• The set-difference operation finds tuples that are in one relation but are not in another
• Notation: $r – s$
• Assumptions:
  • $r, s$ have the same arity
  • Attributes of r and s are compatible

Ex_

---

Assignment Operation: ⬅️

• It is convenient at times to write a relational-algebra expression by assigning parts of it to temporary relation variables
• Notation: ⬅️
• With the assignment operation, a query can be written as a sequential program

Ex_

---

Rename: ρ

• The rename operator, r, sets names to relational-algebra expressions
• Notation: $ρ_{new\_name}(E)$ E : Entity ( Relation or Attribute )

HGU 전산전자공학부 홍참길 교수님의 23-1 Database System 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.

Example problem

Find the records of the instructor(s) who get(s) the largest salary

$tmp_1$ ⬅️ $ρ_{inst1}(instructor) × ρ_{inst2}(instructor)$
$tmp_2$ ⬅️ $σ_{inst1.salary < inst2.salary}(tmp_1)$
$tmp_2$ ⬅️ $∏_{inst1.ID, inst1.name, inst1.dept\_name, inst1.salary}(tmp_2)$
A. $instructor - tmp_3$