[논문 리뷰] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Paper

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

개요

각 layer의 input은 network parameter가 변함에 따라 분포가 달라진다. 만약, saturating activation을 사용하는 경우 학습과정에서 손쉽게 gradient vanishing problem이 발생할 수 있다.

이렇게 학습 과정에서 network parameter가 변함에 따라 layer들의 input distribution이 변하는 현상을 Internal Covariate Shift이라 한다.

Internal covariate shift을 줄이기 위해, layer inputs x에 대한 distribution을 fix하면 된다. 이러한 과정을 whitening process이라 한다.

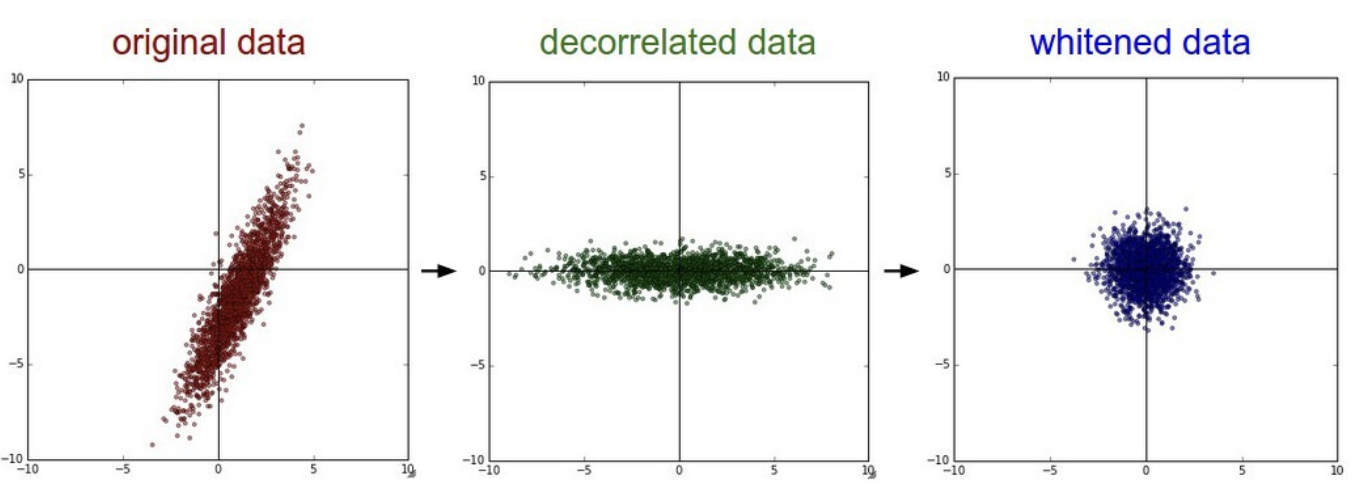
위 그림과 같이, 평균을 0으로, 분산을 1로 맞추는 과정이 whitening process이라 할 수 있다.

하지만 모델의 layer input distribution이 항상 fixed distribution(평균 0, 분산 1)을 따르도록 하는 것에는 치명적인 문제가 발생한다. 바로, Normalization Layer에서 Gradient Descent의 의미가 없다는 것이다.

Normalization Layer의 input을 u라 하고, Normalization Layer에서는 input에 bias b를 더한다. Normalization Layer의 output x의 식은 다음과 같이 적을 수 있다.

Gradient Descent을 적용시켜서 $b\leftarrow b+\Delta b$로 업데이트 한다고 해보자. 하지만 Normalization Layer의 output은 다음 식을 따르며, 변하지 않는다.

이런 일이 발생하는 이유는 Gradient Descent 과정에서 Normalization Layer가 중간에 있다는 것을 고려하지 않았기 때문이다. 이를 해결할 수 있는 방법은, 모델의 parameter에 상관없이 항상 같은 분포의 layer inputs을 갖도록 하면 된다.
(위에서 설명한 잘못된 Normalization 부분에서는 모델의 parameter가 변함에 따라 bias가 함께 변해야 했다.)

---

$x$을 Normalization Layer input이라 하고, $X$을 set of inputs over training dataset이라 하자.
우리는 normalization tramsformation을 다음과 같은 함수로 정의할 수 있다.

현 testdata의 분포 뿐 아니라, 전체 test dataset의 분포에도 영향을 받는다. 여기서 $\text{Norm}$ 함수는 다변수 함수이기 때문에 Jacobian을 통해 gradient을 계산하고, Covariance을 구해야 하기 때문에 계산과정이 복잡해진다.

이러한 문제를 해결하기 위해 논문에서 적용한 방법들은 다음과 같다.

1. layer input vectors을 정규화 하는 것이 아니라, layer input vector의 feature scalars에 대해 정규화를 진행했다. 이를 통해 복잡한 Jacobian, Covariance 계산을 없애 계산량을 줄일 수 있게되었다.

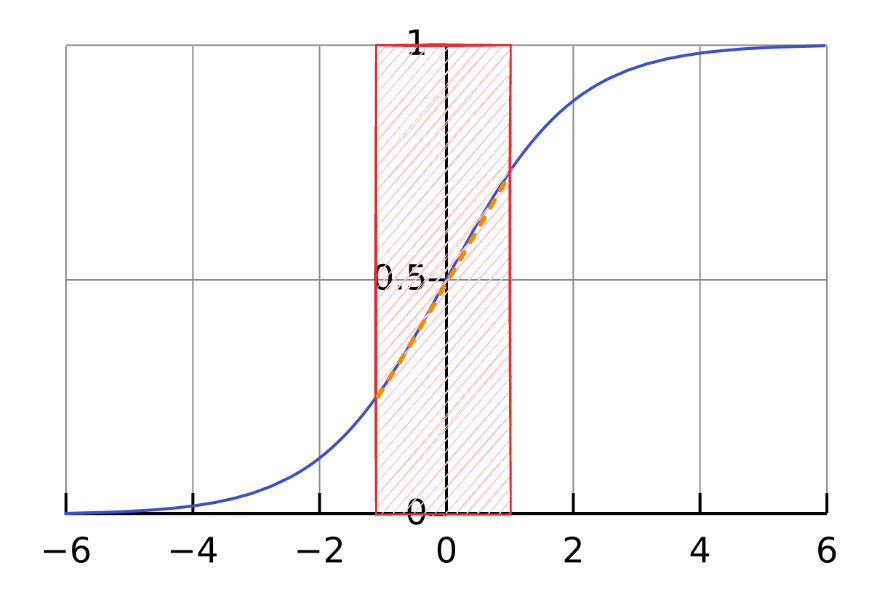
하지만 이렇게 되면 문제가 되는 부분이 생긴다: activation에서 적용시키는 non-linearity 성질을 잃게 된다는 점이다. data distribution이 평균 0, 분산 1이기 때문에 sigmoid activation을 사용하면 아래 그림에서의 주황색 선에 대부분의 데이터들이 존재할 것이며 이는 linear로 근사될 수 있다. 이러한 문제점 때문에 Normalization 단계에서 단순히 평균 0, 분산 1로 정규화 하는 것이 아니라 scale, shift을 해주는 learnable parameter를 추가해줘야 한다.

---

다음으로 SGD로 parameter을 학습시킬 때, mini-batch 단위로 학습된다. 이와 마찬가지로 normalization도 mini-batch data들의 mean, variance을 기준으로 normalize시키는 것이다.

---

최종적으로 Batch Normalization은 다음과 같이 이루어진다:

BN Layer도 학습이 필요한데, 그에 대한 Backpropagation은 chain-rule을 통해 다음과 같이 표현가능하다.

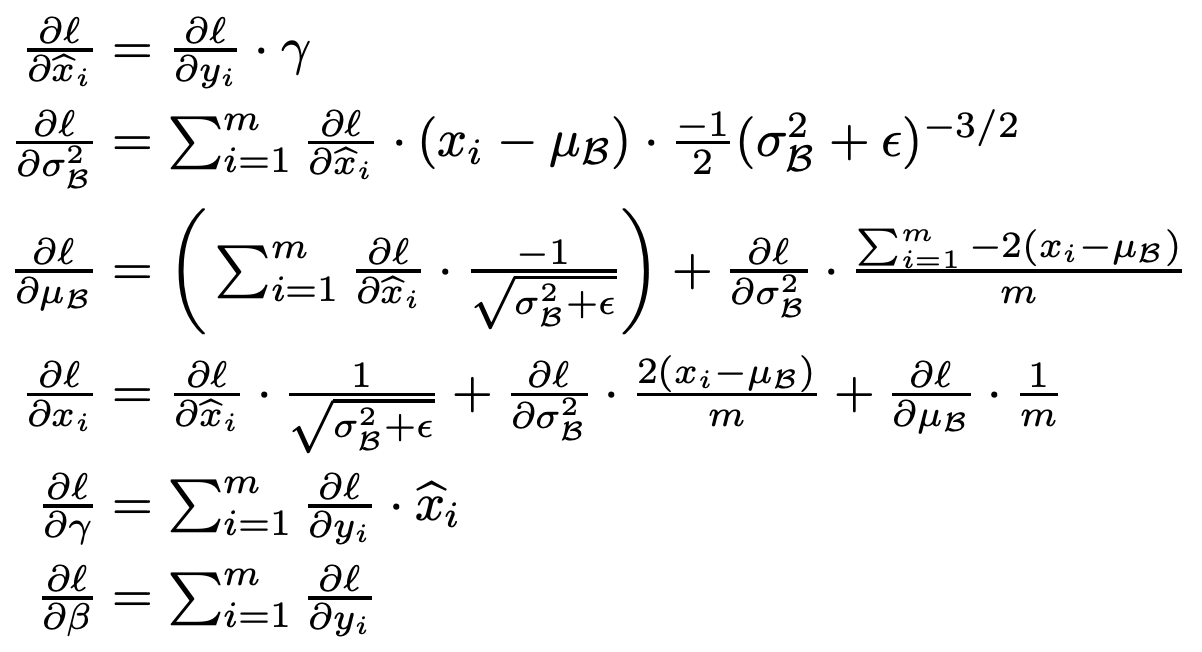
느낀점

논문을 읽고 이해하는 과정이 조금 어려웠다. 하지만 논문에서 Batch Normalization이 필요한지, 이전의 방법들이 왜 문제가 되었는지 등을 친절하게 설명해줘서 많은 것들을 배울 수 있었다. 당연하게 사용하는 Batch Normalization의 논문을 읽는 것이 재밌었다.