Data Structure(Graph)

2020-12-09

새삼느끼는 일이지만, 무엇을하든 미루거나 딴짓을 하면, 내가 몹시 힘들어진다 하하핳 제발 딴짓 좀 그만하고, 매순간이 집중력 MAX였으면 좋겠다,,,ㅜㅜ 인간은 언제나 실수를 반복하지...오늘만큼은 하지말자 JEBAL,,,!

자, 그럼 Graph에 대해서 알아보자!

---

About Graph

---

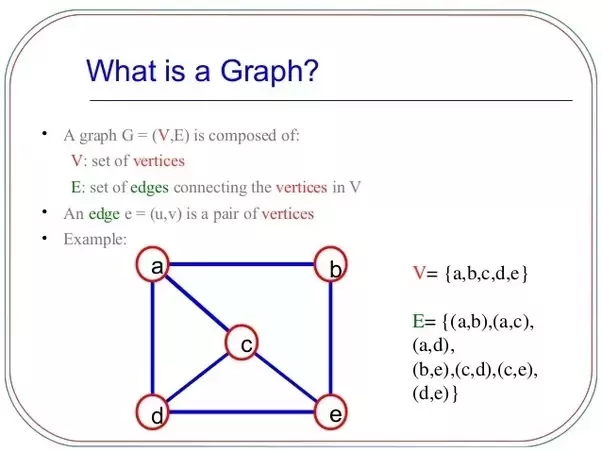
그래프는 쉽게 말해, 네트위크 구조를 추상화한 것이다.컴퓨터 과학에서 항목들이 서로 어떻게 연결되어있는지를 모형화하는 방법으로, Social Network,도로,통신망 등을 표현할때 활용된다. Graph를 이용해서 특정 vertex(node),arcs(edge),path를 검색하고, 최단경로찾기 등의 문제를 해결할 수 있다. Graph는 edge로 연결된 vertex의 집합으로 구성되어있고, vertex와 edge로 연결관계를 표현한 Data Structure이다.

각 vertex들이 서로 연결되어있는 자료구조형인 Graph는 실제로 Trees자료구조를 포함하고 있고, Trees 안에는 Linked List가 포함되어있다. 즉, Graph가 상위개념으로 포괄하고 있는 자료구조형이다. Graph를 보면, Undirected일 수 있는데, 이 말은 edge에 의해서 연결된 node가 서로 대칭일 수 있다는 뜻이다. Directed는 비대칭관계를 의미한다.

---

About Terms & Concepts

---

아래의 그림을 보면, Graph와 Tree의 차이도 볼 수 있지만, Graph의 특징도 잘 나와있다. Tree에서도 보았지만, 좋은 것은 한번 더 보자!👍🤩

Differences between Graph & Tree

Terms

Vertex(= Node, 정점) - 위치
Arcs(= edge, 간선) - 위치간의 관계 / Vertex를 연결하는 선(link)
Adjacent Vertex(인접ㅂ정점) - edge에 의해 직접연결된 Vertex
degree(정점의 차수) - Undirected Graph에서 하나의 vertex에 인접한 vertex의 수
//// Undirected Graph에 있는 Vertex의 모든 degree의 합 = edge 수 * 2
In-degree(진입차수) - Directed Graph에서 외부에서 안으로 들어오는 edge의 수(내차수)
Out-degree(진출차수) - Directed Graph에서 안에서 외부로 향하는 edge의 수(외차수)
//// Directed Graph에 있는 Vertex의 in-degree or out-degree의 합 = Directed graph의 edge의 수(In-degree + Out-degree)
Path Length(경로길이) - path를 구성하는데 사용된 edge의 수
Simple Path(단순경로) - path 중에서 반복되는 vertex가 없는 경우
Cycle(사이클) - Simple Path의 시작 vertex와 종료vertex가 같은 경우

Types of Graph

---

Undirected Graph	Directed Graph
edge를 통해 양방향으로 갈 수 있다.	edge 자체에 방향성이 존재한다.
vertex A와 B를 결하는 edge는 (A,B)와같이 vertex의 쌍으로 표현한다. (A,B) = (B,A) (Ex) 양방향통행도로	A ----> B 로만 갈 수 있는 edge는 <A,B>로 표시 <A,B> !== <A,B> (Ex)일방통행
Connected Graph
Undirected Graph에 있는 모든 vertex 쌍에 대해 항상 경로가 존재하는 경우 ex) tree : cycle을 가지지않는 Connected Graph
Unconnected Graph
Undirected Graph에서 특정 vertex 쌍 사이에 경로가 존재하지 않는 경우

---

Cycle Graph	Acyclic Graph
Simple path의 시작 vertex와 종료 vertex가 동일한 경우	Cycle이 없는 graph
Simple path의 경로중에 반복되는 vertex가 없는 경우

---

Complete Graph	Undirected complete Graph
Graph에 속해있는 모든 vertex가 서로 연결되어있다.	vertex의 수: n이면, edge의 수: n*(n-1)/2

---

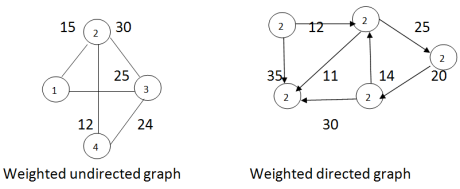
• Weighted Graph(가중치 그래프)
  egde에도 Data value나 가중치가 할당된 graph. Network라고도 한다. ex) 도시-도시연결, 도로길이,통신망사용료
• Unweighted Graph(균일그래프)
  가중치가 없는 그래프를 균일 그래프(unweighted graph)라 한다.

---

Graph Traversal

---

그래프 순회란 처음 vertex을 방문한 이후 아직 탐사할 vetex가 남아있는지 계속 추적하는 일이다. 어떤 정점이 있는지, 두 정점사이의 경로를 찾기, 그래프가 연결되었는지, 사이클이 존재하는 지 등을 확인할때 그래프를 순회한다.

그래프를 순회하는 방식에 따라 '너비 우선 탐색(BFS)', '깊이 우선 탐색(DFS)'으로 나뉜다.

각 순회 방식은 아래 별도의 포스트로 정리한다.

너비 우선 탐색 BFS

간선을 따라 너비 방향으로 먼저 방문하고, 그 다음 아래로 내려가며(깊이 방향으로) 방문하면서
아직 방문하지 않은 정점을 방문 큐에 추가하고 그 큐를 참조하여 정점을 찾아가면서 인접정점을 방문한다.

깊이 우선 탐색 DFS

시작 정점에서 한 방향으로 갈 수 있는 가장 먼 경로까지 깊이 탐색해가다가 더 이상 갈 곳이 없으면 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 간선으로 탐색을 계속함으로써 모든 정점을 방문하는 순회 방법이다.

---

Graph의 Property & Method

구현하는그래프는 무방향 그래프이고, 인접 리스트 (Adjacency List) 방식으로 구현했다.

Property

constructor() {
    /*
     *  ex)
     *    nodes = {
     *      0: [ 1, 2 ],
     *      1: [ 0 ],
     *      2: [ 0 ]
     *    }
     */
    this.nodes = {};
  }

Method

addNode(node) - 그래프에 노드를 추가합니다.
addEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선을 추가합니다.
removeNode(node) - 그래프에서 노드를 삭제합니다.
removeEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선을 삭제합니다.
hasEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선 존재 여부를 반환합니다.
contains(node) - 그래프에 해당 노드가 존재하는지 여부를 반환합니다.

  addNode(node) { //그래프에 node 추가
    this.nodes[node] = this.nodes[node] || []; 
    // 단축평가 = shortcut circuit 둘중에 하나만 맞으면 true 
  }

  contains(node) {
    //hasOwnProperty : 키가있는지 확인 > t/f return 
  }

  removeNode(node) {
    // 노드가 있으면
      // 노드 삭제
    
    // 아니면 말고
  }



  hasEdge(fromNode, toNode) {
    // fromNode와 toNode 사이의 간선 존재 여부를 반환합니다.
    // fromNode와 toNode가 서로 포함되어있어야 간선이 존재
    // 방향성이기 때문에 
    
    // node가 존재하면
      // fromNode가 toNode를 include
    
    // 아니면 false
  }

  addEdge(fromNode, toNode) { // 간선추가
   //fromNode에 toNode push
   //toNode에 fromNode push
  }

  removeEdge(fromNode, toNode) { //간선삭제
    //fromNode toNode번 index에서 1개 요소 제거
    //toNode fromNode번 index에서 1개 요소 제거
  }