Data Structure(Tree)

2020-12-09

밀린만큼 밤새더라도, tree까지 올리고 잘거다.. 밀리지말자ㅜ

자, Tree에 대해서 알아보자!!

---

About Tree

---

Tree 구조는 나뭇가지가 펴져나가는 형태의 node로 이루어진 자료구조인데, 나무를 뒤집어놓은 모양이라고 하여 Tree라고 부른다. 가장 위에 있는 node를 root라고 부르고, 그 아래로 가지를 치며 내려오는 구조다. 그래프 자료구조의 특수한 형태로 보기도한다.

Tree는 parentNode - ChildNode로 계층구조를 추상화해, 정보를 쉽게 검색하기 위해, 저장할때 유용한 구조이다. 쉽게 회사조직도, 가계도를 생각해보면 된다. 계층구도를 추상화했다고 볼 수 있겠다.

Tree는 Parent-Child 관계를 가지는 nodes로 구성되었고, 각각의 node는 1개의 parentNod, 여러개의 ChildNode를 가질 수 있다.

---

About Terms & Concepts

---

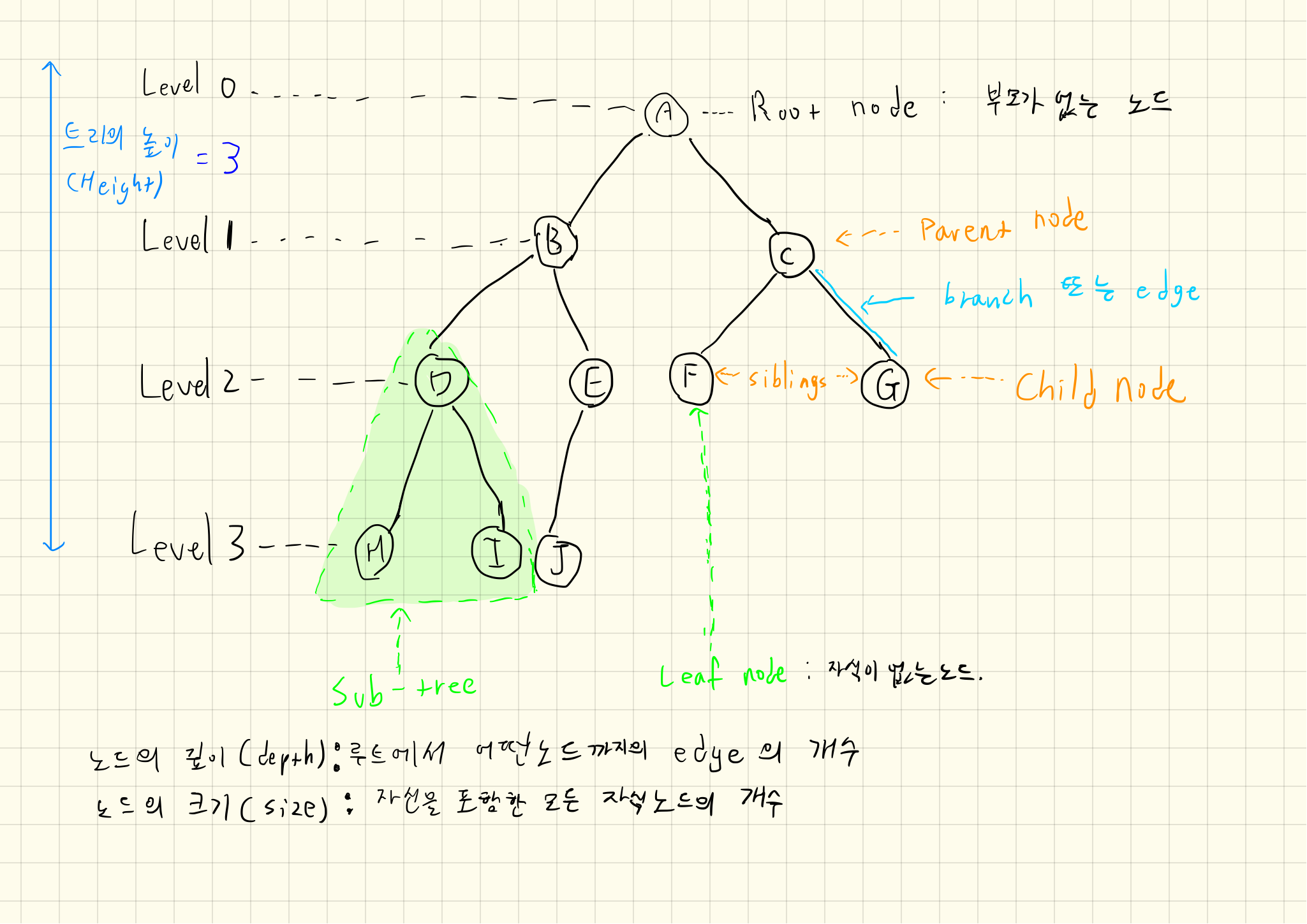
Concepts

1. Tree는 하나의 root node를 갖는다.
2. root node는 0개 이상의 child node를 갖는다.
3. 그 child node 또한 0개 이상의 child node를 갖고 있고, 반복적으로 정의된다.

아래의 graph와 Tree의 차이점을 잘 숙지하자.

Terms

노드(node) : tree를 구성하는 각 요소. key, left pointer, right pointer로 구성되어있다.
루트 노드(root node) : 부모가 없는 최상위 노드, 트리는 하나의 루트 노드만을 가진다.
단말 노드(leaf node) : 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
내부 노드(internal node) : 단말 노드가 아닌 노드
간선(edge) : 노드를 연결하는 선 (link, branch 라고도 부름)
형제(sibling) : 같은 부모를 가지는 노드
노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합
노드의 차수(degree) : 노드가 지닌 가지의 수
트리의 차수(degree of tree) : 트리의 최대 차수
트리의 높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이

---

Type of Tree

---

1. Tree vs Binary Tree

Binary Tree(이진 트리)는 각 node가 최대 2개의 자식을 갖는 tree이다. 모든 tree가 이진트리는 아니다. 특히 컴퓨터 과학에서 Binary Tree를 자주 활용한다. node의 삽입, 조회, 삭제를 효과적으로 수행할 수 있기 때문이다.
여기서 Tree가 가지고 있는 하나의 node를 코드로 적으면 아래와 같다.

function BinaryTreeNode(value){
  this.value = value;
  this.left = null;
  this.right = null;
}

Binary Tree는 순회하는 방법이 세가지가 있다.

1. 중위순회(inorder traversal) : 왼쪽 > 부모 > 오른쪽
   
   
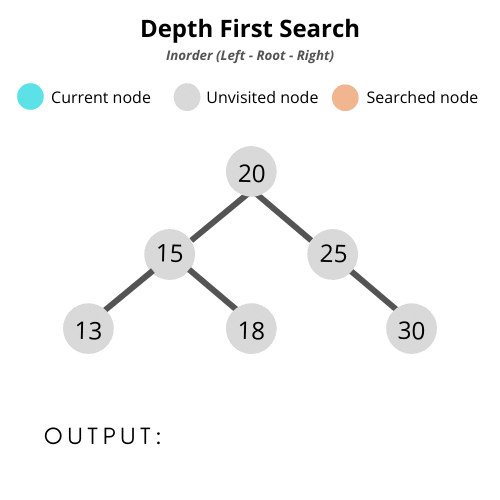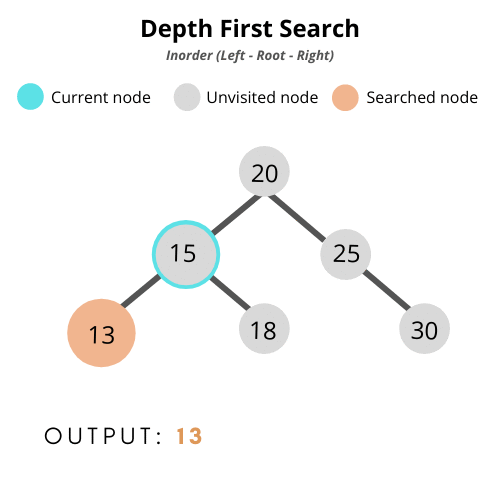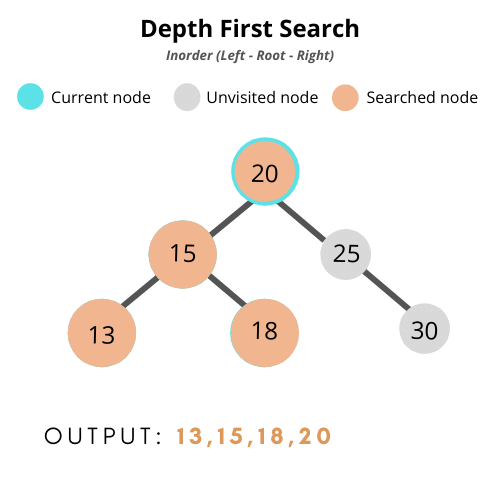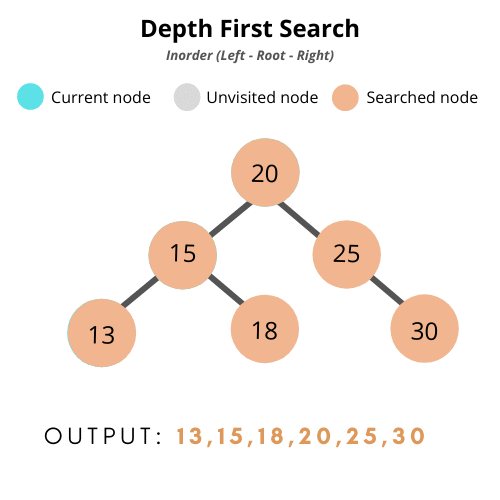
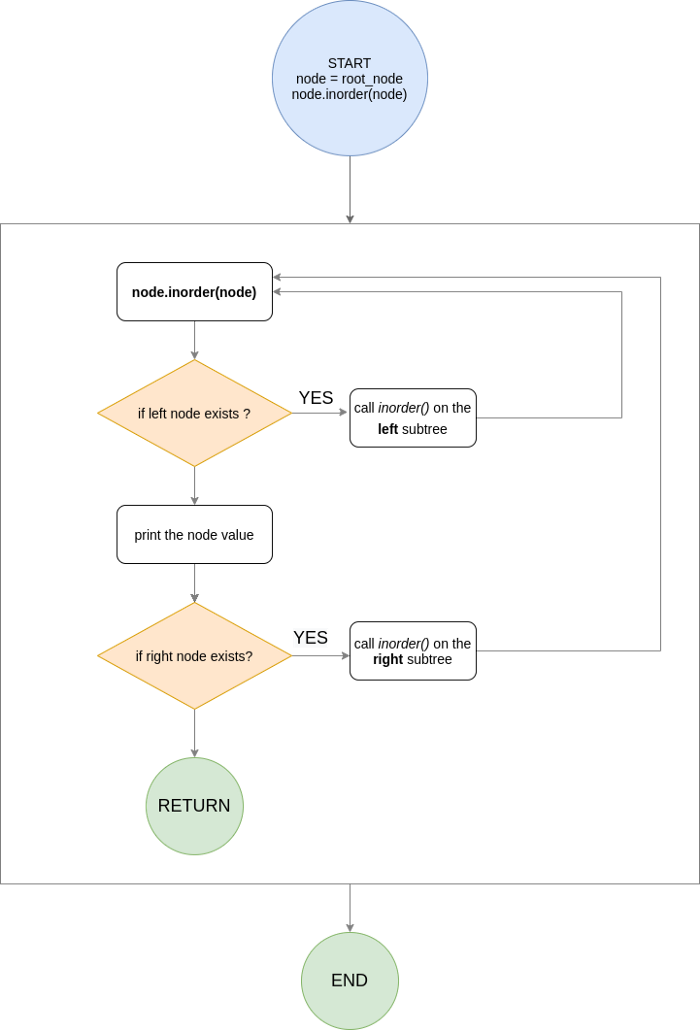
2. 전위 순회(pre-order traversal): 부모 > 왼쪽 > 오른쪽
   
   
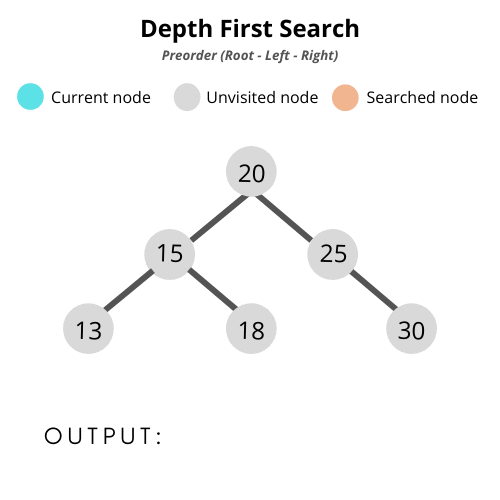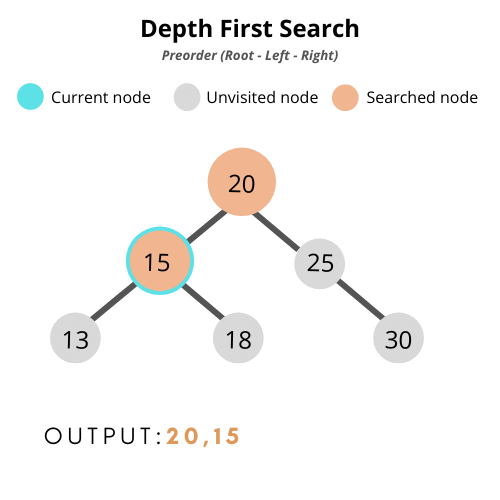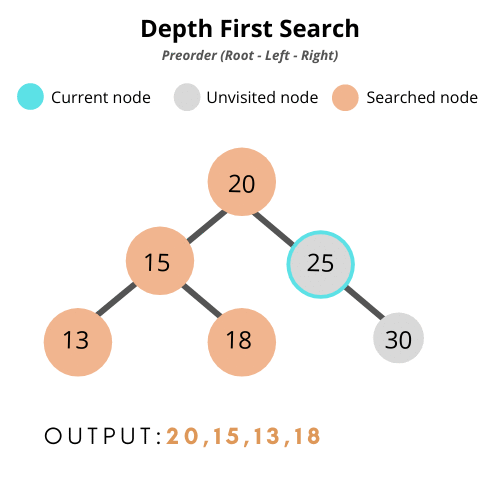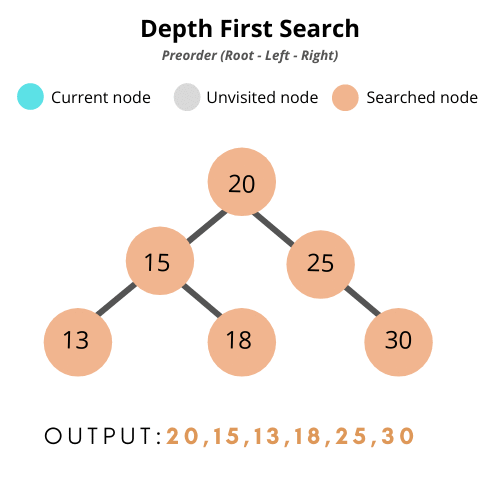
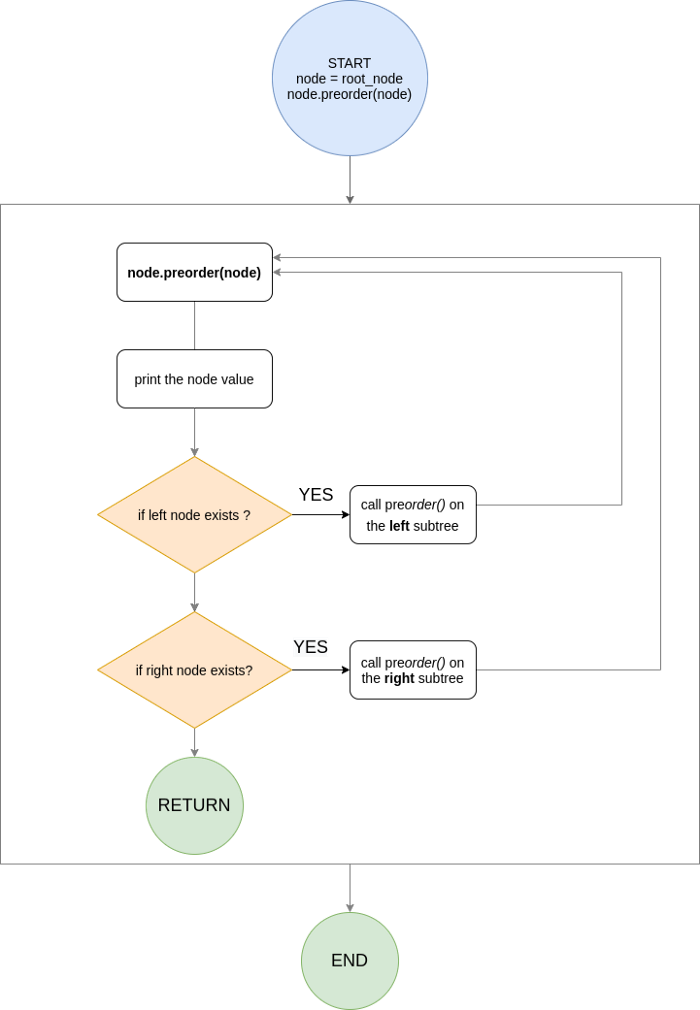
3. 후위 순회(post-order traversal): 왼쪽 > 오른쪽 > 부모
   
   

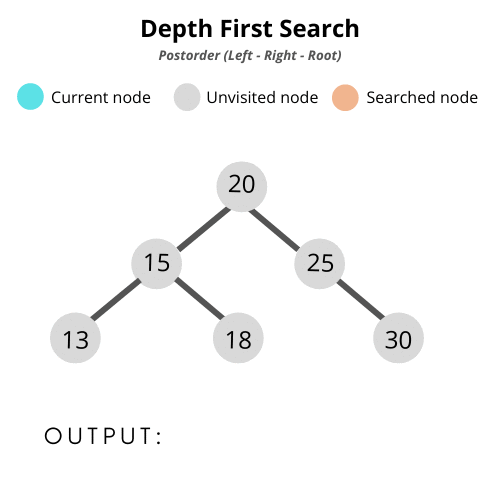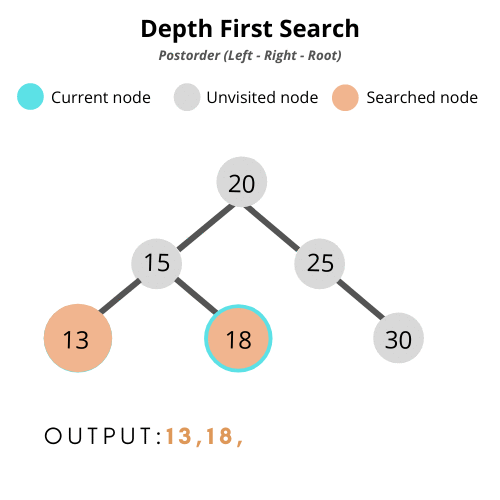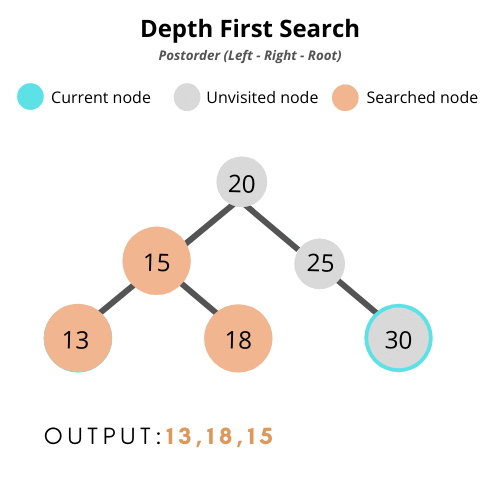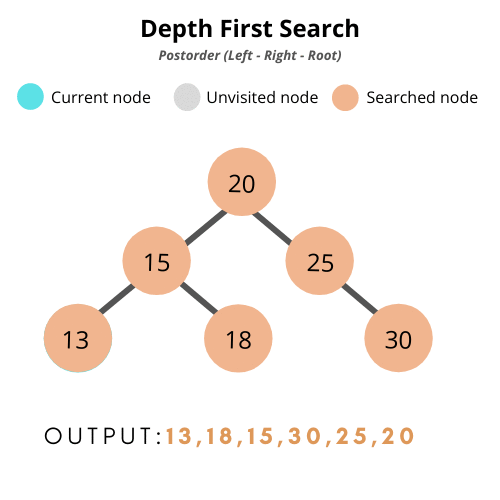
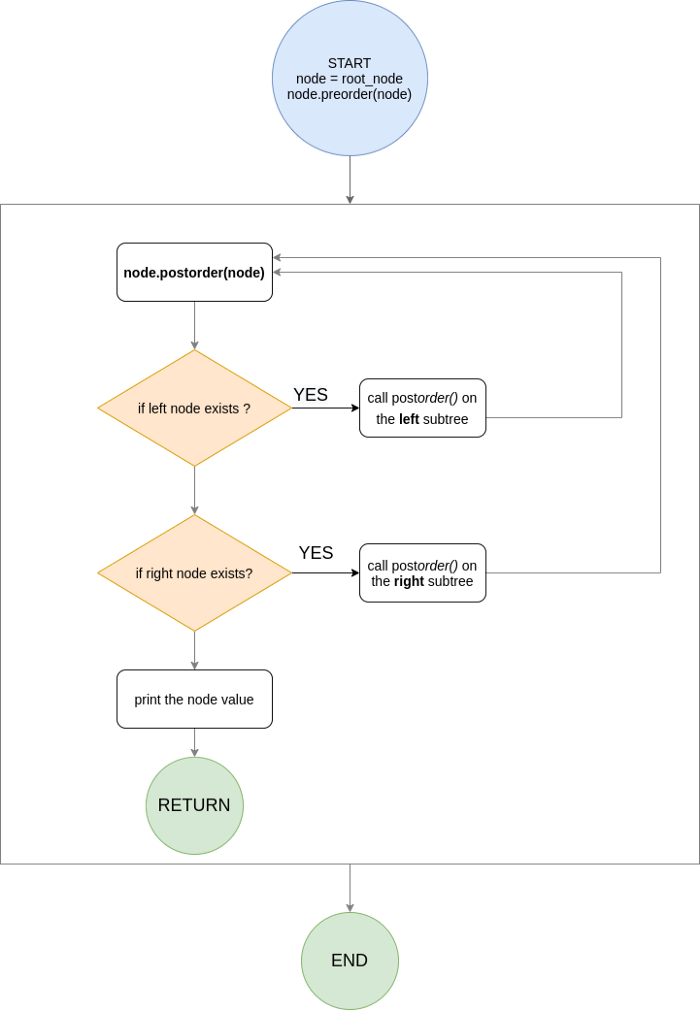
2. Binary Search Tree

이진 탐색 트리(Binary Search Tree)는 모든 노드가 아래와 같은 특정 순서를 따르는 속성이 있는 이진 트리다. 모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)

3. Complete Binary Tree vs Full Binary Tree vs Perfect Binary Tree

Complete Binary Tree

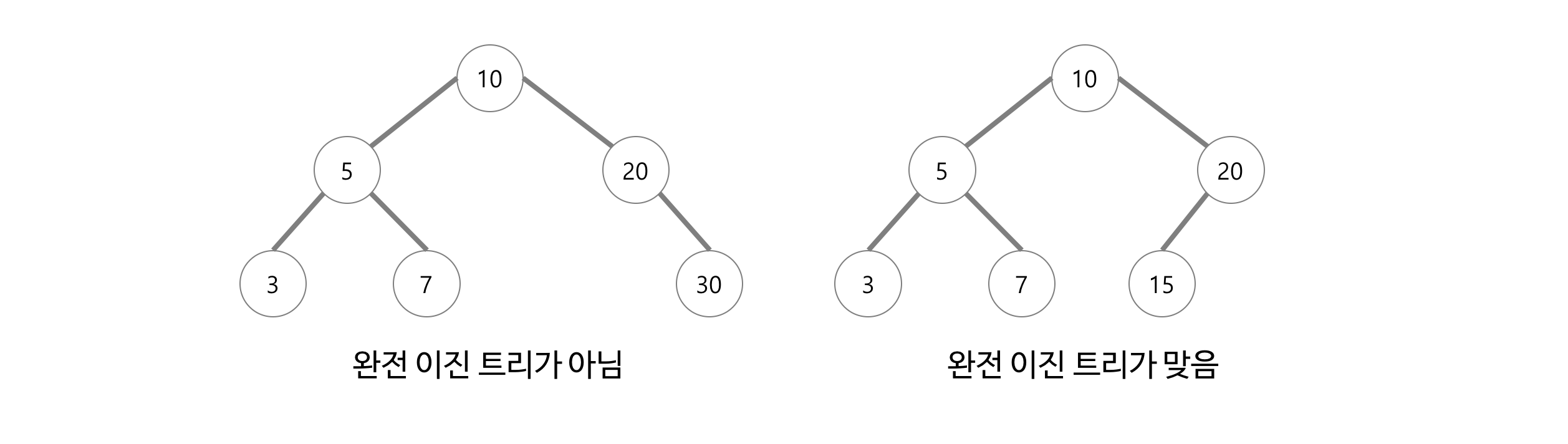
완전이진트리는 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리이다. 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다. 마지막 레벨은 꽉 차 있지 않아도 되자만 노드가 왼쪽에서 오른쪽으로 채워져야 한다. 마지막 레벨 h에서 (1 ~ 2h-1)개의 노드를 가질 수 있다.
또 다르게 말하면, 가장 오른쪽의 잎 노드가 (아마도 모두) 제거된 포화 이진 트리다. 완전 이진 트리는 배열을 사용해 효율적으로 표현 가능하다.

Full Binary Tree

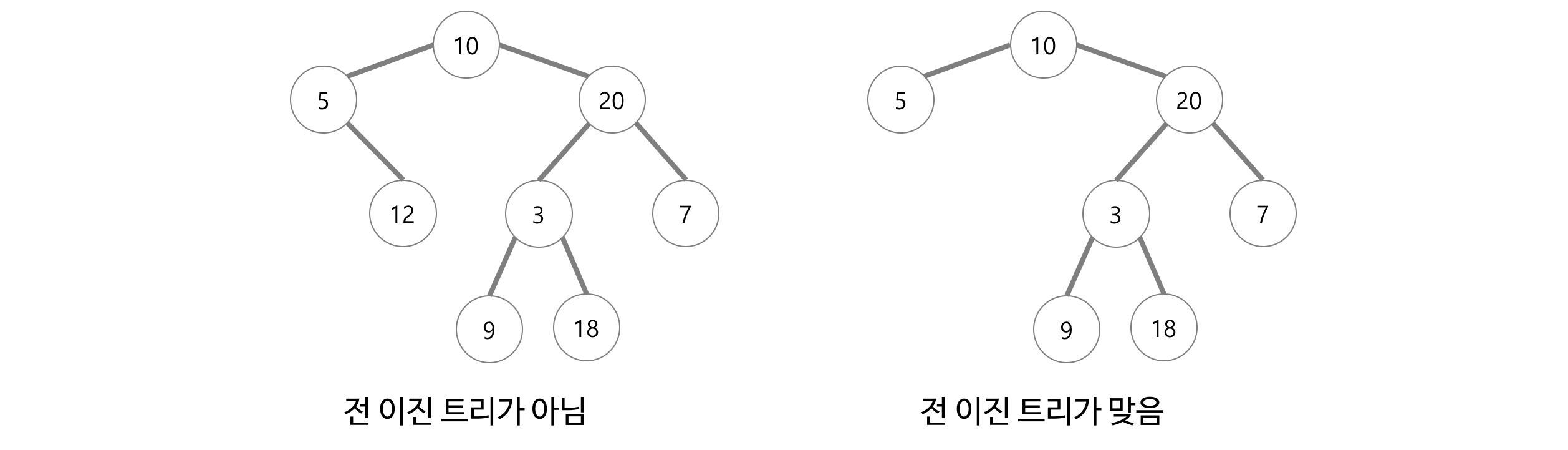
전이진트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.

Perfect Binary Tree

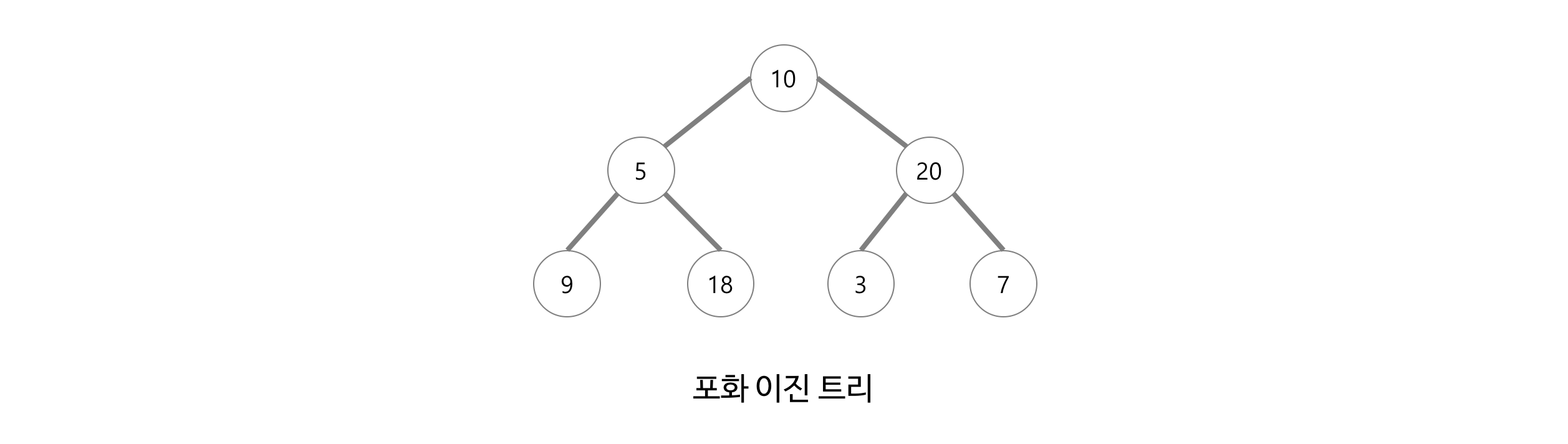
포화이진트리는 전 이진 트리이면서 완전 이진 트리인 경우를 말한다. 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다. 모든 내부 노드가 두 개의 자식 노드를 가진다. 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다. 노드의 개수가 정확히 2^(k-1)개여야 한다.

---

Tree의 Property & Method

Property

this.value = value;
this.children = [];

Method

insertNode(value) - 트리에 노드를 추가합니다.
contains(value) - 트리에 해당 노드가 존재하는지 여부를 반환합니다.

insertNode(value) {
    // 새로운 node 생성 
    // children에 node를 추가
  }

  contains(value) {
    // 첫 객체 안에 value가 있으면
      // return true
    // value가 없으면 
      // children을 돌면서 
        // 재귀로 children 안의 value를 확인
          //  있으면, return true
      // 아니면 return fals
  }

Binary Search Tree의 Property & Method

Property

this.value = value;
this.left = null;
this.right = null;

Method

insert(value) - 이진 탐색 트리에 노드를 추가합니다.
contains(value) - 이진 탐색 트리에 해당 노드가 존재하는지 여부를 반환합니다.
inorder(callback) - 이진 탐색 트리를 중위순회 합니다.

  insert(value) {  // insert(value) - 이진 탐색 트리에 노드를 추가합니다.
    // 노드를 생성
    // 들어오는 value가  this.value보다 작으면
      // this.left가 null일때
        // this.left에 node 생성
      // 그 외에
        // 재귀로 돌리기
      
    // 들어오는 value가 this.value보다 크면
      // this.right가 null 일때 위의 this.left부분과 동일
  }

  contains(value) {// 이진 탐색 트리에 해당 노드가 존재하는지 여부를 반환.
    // this.value값 확인
      // 맞으면 return true
    // this.value가 value보다 작으면
      // this.right이 null일때
        // return false;
      // 오른쪽 끝까지 재귀로 돌기
        // return true;
      
    // this.value가 value보다클때
      // this.left부분 위의 right과 동일

    // return false;
  }

  inorder(callback) {//이진 탐색 트리를 중위순회 합니다.
    // this.left값이 null이 아니면, this.left를 계속 타고 내려간다.
    // this.value callback 실행
    // this.right값이 null이 아니면, this.right를 계속 타고 내려간다.
  }

참고사이트
사진참고사이트