Today I Learned
오늘은 행렬에 대해 배웠다.
행렬(Matrix)

x(볼드체 소문자)는 행 벡터. 그냥 x는 벡터 안의 원소(스칼라)
-
벡터 : 숫자를 원소로 가지는 1차원 배열
-
행렬 : 벡터를 원소로 가지는 2차원 배열
-
행(row)과 열(column)이라는 인덱스를 가진다. Xij = i번째 행과 j번째 열에있는 원소
import numpy as np
# 3개의 행 벡터를 하나의 array에 담은 행렬
# numpy에선 행(row)이 기본 단위
x = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
전치행렬(transpose matrix)
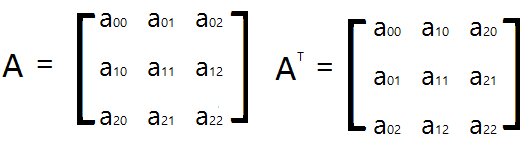
-
행과 열의 인덱스가 바뀐 행렬. 대각선을 기준으로 뒤집는다.
-
행렬 위에 T를 붙임
-
numpy에선 X의 전치행렬은 X.T로 표현하면 된다.
행렬의 이해
-
벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타낸다.
-
행렬의 행벡터 Xi는 i번째 데이터(집합)를 의미한다.
Xij는 i번째 데이터의 j번째 변수 -
행렬끼리 같은 모양이면 덧셈과 뺄셈을 계산할 수 있다. 행렬의
성분곱도 벡터와 같이 각 인덱스 위치끼리 곱하면 된다. 각 위치의 원소들끼리 덧,뺄, 곱셈을 하면 된다. -
스칼라곱도 벡터와 차이가 없이 모든 성분에 똑같이 숫자를 곱해주면 된다.
행렬 곱셈(matrix multiplication)
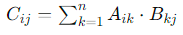
-
i번째 행 벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.
즉, 앞의 행벡터와 뒤의 열벡터를 곱한 결과값들을 정리한 것이다. -
행렬곱셈은 X행렬과 Y행렬의 곱셈일 때, X의 열의 개수와 Y의 행의 개수가 같아야한다.
X가 3 X 4이고, Y가 4 X 2면 XY는 3 X 2의 크기를 갖는다. -
행렬 곱셈은 XY와 YX가 결과가 다르다. 순서에 따라 결과가 달라진다.
-
numpy 사용시 행렬곱셈은
@연산자를 사용한다.
import numpy as np
x = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
y = np.array([[0, 1],
[1, -1],
[-2, 1]])
result = x @ y
print(result)
# 1*0 + -2*1 + 3* -2 = -8
'''
[[-8 6]
[ 5 2]
[-5 1]]
'''행렬의 내적
-
numpy의
np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. 즉, 앞의 행벡터와 뒤의 행벡터의 곱을 정리한 것이다. -
두 행렬의 행의 크기가 같아야한다.
-
여기서 numpy의 내적(inner)은 수학에서 말하는 내적과는 다르다.
import numpy as np
mat1 = np.array([[1, 2], [3, 4]])
mat2 = np.array([[5, 6], [7, 8]])
result = np.inner(mat1, mat2)
print(result)
'''
[[17 23] # (1 * 5) + (2 * 6) = 17 / (1 * 7) + (2 * 8) = 23
[39 53]] # (3 * 5) + (4 * 6) = 39 / (3 * 7) + (4 * 8) = 53
'''본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.
