Today I Learned

오늘은 행렬을 다른 시각으로 접근하는 방법에 대해 학습했다.

행렬의 다른 이해

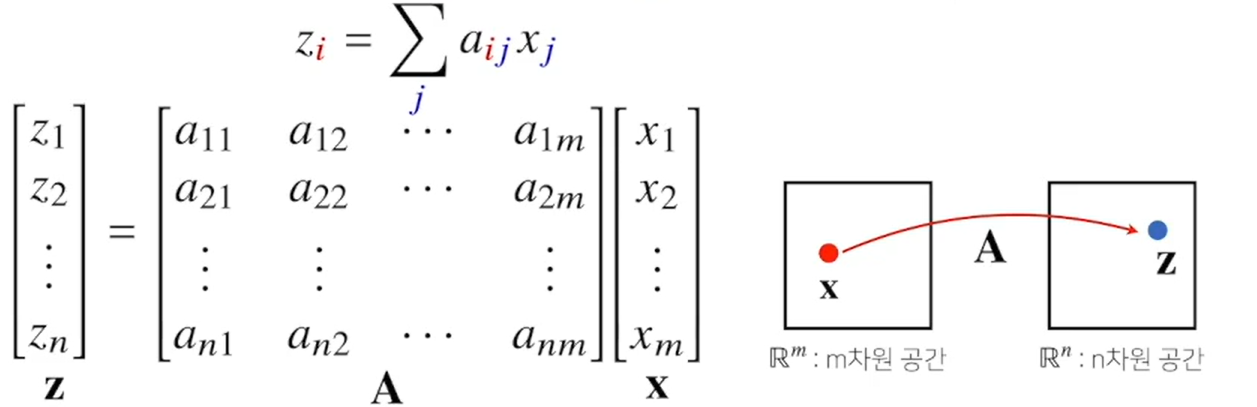
• 위와는 다르게 행렬을 데이터로 보지 않고, 서로간의 다른 두 데이터를 연결시키는 연산자(operator)로 이해할 수도 있다.

• 행렬 곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.

• 위의 그림처럼 A 행렬과 x 열벡터를 곱하면 z 라는 새로운 열벡터가 나온다.
  즉, z와 x라는 벡터를 A라는 행렬이 서로 이어주는 연산자 역할을 하게 된다.

• 행렬곱을 통해 주어진 데이터에서 패턴을 추출할 수 있고, 데이터를 압축할 수도 있다.
  모든 선형 변환(linear transform)은 행렬곱으로 계산할 수 있다.

역행렬(inverse matrix)

어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬

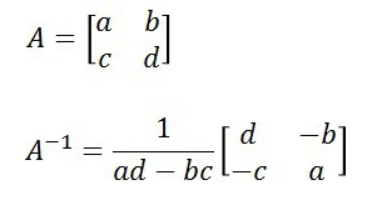
• A의 역행렬을 A^-1로 표기한다.

• 행렬과 역행렬의 곱은 항등행렬 I가 된다. 순서를 바꿔도 결과는 항등행렬(어떤 행렬을 곱해도 결과가 자기 자신, 대각선만 1이고 나머지는 0)이다.

• 조건 : 행과 열 숫자가 같아야 한다. 행렬식(determinant)이 0이 아니어야 한다.

• x -> z로 보낸 결과를 역행렬을 활용해서 z -> x로 되돌아오게 할 수 있다.

• numpy에선 linalg 라이브러리의 inv()함수로 역행렬을 계산할 수 있다.

import numpy as np

B = np.array([[4, 7], [2, 6]])
B_inv = np.linalg.inv(B)

print(B_inv)

유사 역행렬

• 만약에 조건이 맞지않아 역행렬을 계산할 수 없다면 유사 역행렬(pseudo-inverse)또는 무어-펜로즈 역행렬을 이용한다. -1이 아니라 +기호를 쓴다. A^+
  numpy에선 np.linalg.pinv(A)로 계산할 수 있다.

• 행이 열보다 많으면 유사역행렬을 먼저 곱해야하고, 열이 행보다 많으면 유사역행렬을 뒤에 두고 곱해야된다.

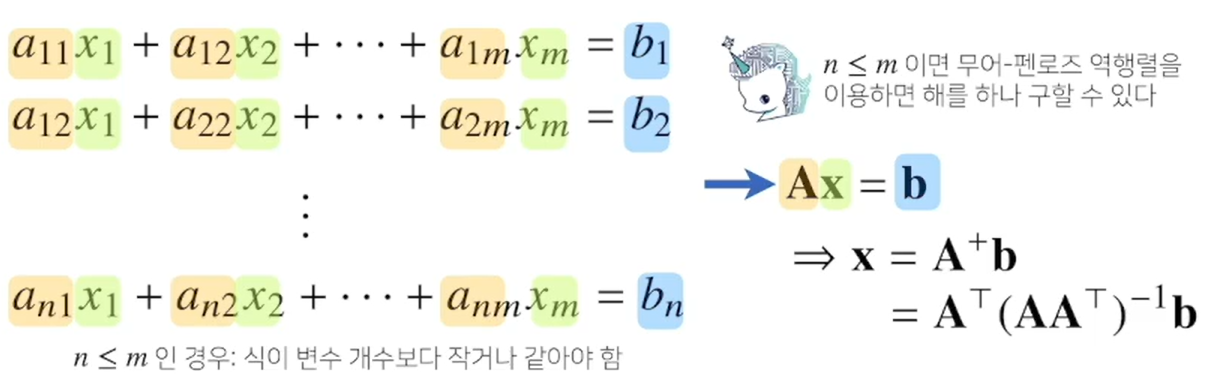
• 계수 열 벡터 A, 구해야 하는 해답 행렬 x, 결과 열 벡터 b로 봤을때 Ax = b로 두고 유사 역행렬을 이용해 연립방정식의 해를 구할 수 있다.

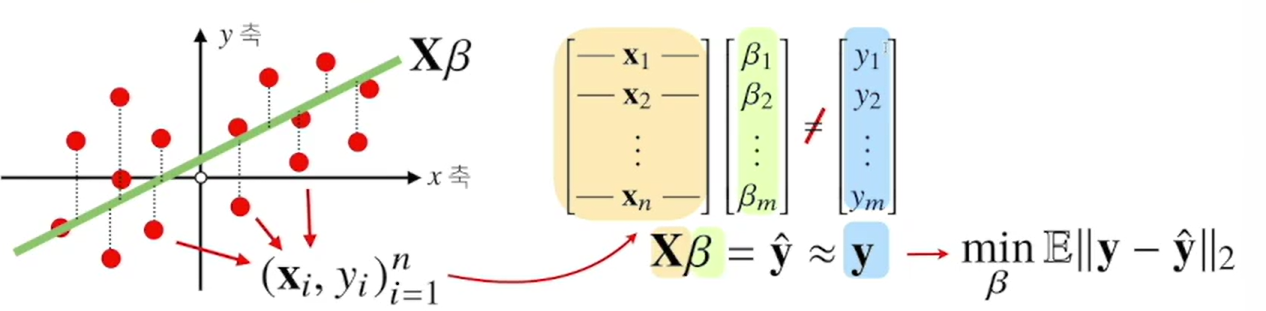
• 무어-펜로즈 역행렬을 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있다. L2-노름을 최소화 하는 계수 베타를 찾는 방식으로 회귀식을 찾는다.

• sklearn의 LinearRegression을 사용하면 선형회귀분석을 쉽게할 수 있다.
  from sklearn.linear_model import LinearRegression

본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.