Today I Learned
오늘은 통계적 모델링 이어서 최대가능도 추정법에 대해 공부했다.
최대 가능도 추정법
Maximum Likelihood Estimation, MLE. 이론적으로 가장 가능성이 높은 모수 추정법
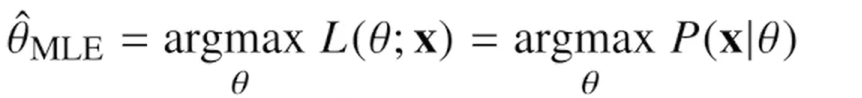
-
가능도 함수(Likelihood Function)
주어진 데이터가 특정 모수 값에 따라 발생할 가능성을 나타내는 가능도 함수를 설정한다. 가능도 함수는 주어진 데이터가 관측될 확률을 나타낸다. -
로그 가능도 함수
데이터 집합 X가 독립적으로 추출되었을 경우엔 로그가능도를 최적화한다. 계산을 더 쉽게 하기 위해 가능도 함수에 로그를 취한 형태다.
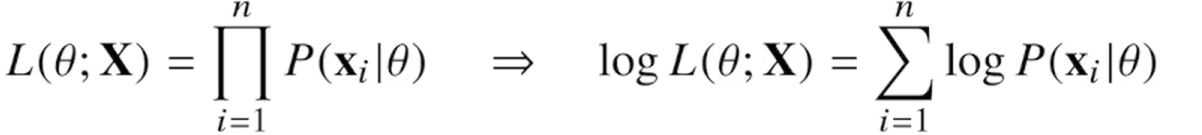
-
로그 가능도를 사용하는 이유? -> 최적화
데이터가 수억단위로 많으면 가능도함수는 연산 오차가 심해진다.
데이터가 독립이면 로그를 씌우면 곱셈이 로그가능도의 덧셈이 되기 때문에 최적화가 된다.
경사하강법을 쓸때 연산량이 O(n^2)에서 로그가능도 사용시 O(n)으로 줄어든다. -
로그 가능도 함수를 최대화하는 μ와 σ를 찾아 미분한다.
python 코드 예시
정규분포
import sympy as sp
import numpy as np
# 데이터
data = np.array([160, 162, 165, 167, 170, 172, 175, 177, 180, 182])
n = len(data)
# 변수 설정
mu, sigma = sp.symbols('mu sigma')
# 가능도 함수의 로그
log_likelihood = -n/2 * sp.log(2 * sp.pi) - n/2 * sp.log(sigma**2) - 1/(2 * sigma**2) * sp.Sum((data - mu)**2, (mu, sigma)).doit()
# 변수 설정
mu, sigma = sp.symbols('mu sigma')
# 데이터 합계 및 제곱 합계
data_sum = np.sum(data)
data_squared_sum = np.sum(data**2)
# 로그 가능도 함수
log_likelihood = -n/2 * sp.log(2 * sp.pi) - n/2 * sp.log(sigma**2) - 1/(2 * sigma**2) * (data_squared_sum - 2 * mu * data_sum + n * mu**2)
# 로그 가능도 함수를 mu와 sigma에 대해 미분
dL_dmu = sp.diff(log_likelihood, mu)
dL_dsigma = sp.diff(log_likelihood, sigma)
# dL/dmu = 0 인 mu 구하기
mu_est = sp.solve(dL_dmu, mu)
# dL/dsigma = 0 인 sigma 구하기
sigma_est = sp.solve(dL_dsigma, sigma)
# mu 값을 171로 대입하여 sigma 값을 계산
sigma_val = sigma_est[1].subs(mu, 171)
sigma_val.evalf()카테고리 분포
import numpy as np
from scipy.optimize import minimize
# 데이터 준비 (예시 데이터)
data = np.array([1, 2, 1, 3, 4, 2, 1, 1, 3, 2, 1, 4, 3, 2, 1, 4, 1, 3, 2, 1])
# 카테고리 수
k = 4
# 초기 확률값 (균등 분포)
initial_theta = np.full(k, 1/k)
# 로그 가능도 함수
def log_likelihood(theta, data):
n = len(data)
log_likelihood_value = 0
for i in range(1, k + 1):
log_likelihood_value += np.sum(data == i) * np.log(theta[i-1])
return -log_likelihood_value # minimize 함수는 최소화하므로 음수로 반환
# 제약 조건 (모든 확률의 합이 1)
constraints = [{'type': 'eq', 'fun': lambda theta: np.sum(theta) - 1}]
# 각 확률이 0 이상이어야 함
bounds = [(0, 1)] * k
# 최적화
result = minimize(log_likelihood, initial_theta, args=(data,), constraints=constraints, bounds=bounds)
# 최적화된 확률값
theta_mle = result.x
theta_mle
딥러닝에서 최대가능도 추정법
-
최대가능도 추정법을 이용해서 기계학습 모델을 학습할 수 있다.
-
원핫벡터로 표현한 정답레이블을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있다.
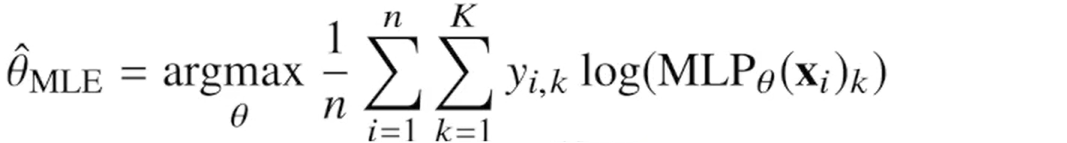
확률분포의 거리
-
기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도된다.
-
데이터 공간에 두 확률 분포 P(x), Q(x)가 있으면 두 확률분포 사이의 거리를 계산할때 총변동거리(TV), 쿨백-라이블러 발산(KL), 바슈타인거리(WD)와 같은 함수를 이용한다.
쿨백-라이블러 발산
-
두 확률 분포 사이의 차이를 측정하는 데 사용되는 비대칭적인 정보 이론적 척도
-
특정 확률 분포 P가 다른 확률 분포 Q와 얼마나 다른지를 나타낸다.
-
이산확률변수
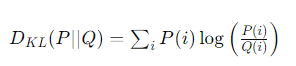
-
연속확률변수
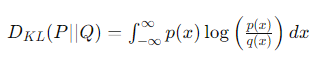
-
분류문제에서 적답레이블을 P, 모델 예측을 Q라고 두면
최대가능도 추정법은 쿨백-라이블러 발산을 최소화하는 것과 같다.
본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.
