Today I Learned

오늘은 통계학에 대해 공부했다.

통계적 모델링

통계적 모델링

적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표.
기계학습과 통계학이 공통적으로 추구하는 목표

• 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 아는 것은 불가능하다.
  근사적으로 확률분포를 추정할 수 밖에 없다.

• 모수적(parametric) 방법론
  데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수를 추정하는 방법

• 비모수적(nonparametric) 방법론
  특정 확률 분포를 가정하지 않고 데이터에 따라 모델의 구조와 모수의 개수가 유연하게 바뀌는 방법. 기계학습에서 많은 방법들은 여기에 속한다. 비모수적 방법론이라 해서 모수가 없는게 아니다. 모수가 무한히 많거나 모수의 개수가 데이터에 따라 바뀔 뿐이다. 차이는 어떤 가정을 미리 하는지 차이.

• 확률 분포 가정 예시

  데이터가 2개의 값(0 or 1) -> 베르누이 분포
  데이터가 n개의 이산적인 값 -> 카테고리 분포
  데이터가 [0,1] 사이 값인 경우 -> 베타 분포
  데이터가 0이상의 값 -> 감마분포, 로그정규분포
  데이터가 R 전체에서 값을 가지는 경우 -> 정규분포, 라플라스 분포

• 단, 기계적으로 확률분포를 가정하면 안되고, 데이터 생성 원리를 먼저 고려해야 한다.

모수 추정(정규분포)

• 정규분포의 모수는 평균과 분산으로, 이를 추정하는 통계량은 아래와 같다.
  표본 분산을 구할때는 N-1로 나눈다.
  

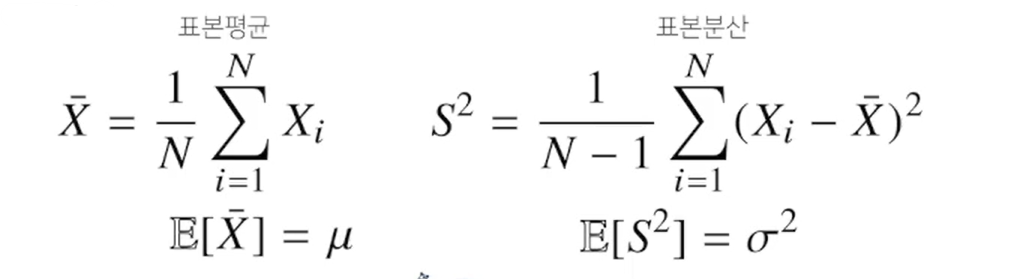
표집분포

Sampling Distribution. 표본 평균과 표본 분산의 확률 분포를 표집분포라 한다.
특히 표본평균의 표집분포는 N이 커질수록 정규분포를 따른다(중심극한정리)

• 표본평균과 표본 분산은 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라진다.

본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.