Today I Learned

오늘 배운 내용은 생성 모델!

Generative Models

주어진 입력 데이터의 확률 분포를 모델링하여 새로운 데이터를 생성하는 모델

• Generation
  확률 모델이 학습한 데이터의 분포를 기반으로 새로운 데이터를 생성하는 과정

• Density Estimation
  주어진 데이터를 기반으로 데이터의 확률 분포를 추정하는 과정(분류 문제와 비슷)
  확률을 얻을 수 있으므로 explicit model이라고도 한다.
  그래서 Generative Model을 완전히 학습했다하면 이는 Discriminative Model을 포함한다.

basic discrete distribution

1. 베르누이 분포 (Bernoulli Distribution)
   하나의 이벤트가 두 가지 가능한 결과 중 하나를 갖는 경우(이진 변수)에 사용된다.
   동전 던지기 같은 p냐 1-p냐의 확률을 가진다.

2. Categorical Distribution
   하나의 시도에서 여러 개의 범주(category) 중 하나를 선택하는 경우(다항 변수)에 사용된다.
   주사위 던지기나 주식종목 선택같은 경우에 사용된다.

Conditional Independence

• RBG를 모델링하기 위해서는 각 색깔당 256, 즉 약 256x256x256개의 파라미터가 필요하다.
  흑백의 binary image라도 n개의 픽셀이면 2^n개의 state가 발생한다.

• 모든 픽셀이 independent하다고 생각하면 state는 여전히 2^n.
  n개가 모두 독립적으로 있으므로 이 distribution을 표현하기 위해서 필요한 파라미터의 수는 n개다. 하지만 현실적으로 모두 독립되어있지 않기 때문에 이 중간이 필요하다.

• 조건부 독립성은 변수가 주어진 조건 하에서 독립적인지를 나타내는 개념이다. 두 변수가 주어진 조건 하에서 서로 독립적이라면, 이는 이 두 변수가 조건부로 서로 영향을 주지 않는다는 것을 의미다.

• Z라는 조건이 주어졌을 때, X와 Y는 independent하다.(기본에 깔린 조건)
  P(X,Y|Z) = P(X|Z) x P(Y|Z)

• chain rule을 생각해 봤을 때, p(x1,..,xn)은 2^n-1개의 파라미터가 필요하다.
  Markov를 가정하면(바로 앞 데이터만 상관있다는 가정) 2n-1개의 파라미터만 필요하다.
  위에서 봤던 대로 완전 independent하다면 n개의 파라미터만 필요하다.
  즉, 조건부 독립성에서 어떤 조건을 거냐에 따라 파라미터를 조절할 수 있다.

Auto-regressive Model

• 자기회귀모델은 현재의 데이터가 이전 시간 단계의 데이터에 종속되어 있다고 가정한다.
  즉, 시간에 따른 데이터의 변화를 자신의 과거 데이터로 설명하는 모델이다.

• 바로 이전의 데이터에만 엮인 Markov도 여기에 속하고, 이전의 모든 데이터와 엮여있다고 봐도 여기에 속한다. 이전의 몇개를 고려하냐에 따라서 arn(ar1, ar3 등)모델이라 한다.

NADE

• 첫번째는 독립적이고, 두번째부터는 이전의 데이터들과 dependent하다.
  즉, i번째 pixel은 i-1개의 입력에 dependent하다.
  i번째 pixel은 1~i-1개의 weight를 받을 수 있어야 한다.

• NADE는 Generation만 할 수 있는게 아니라, 확률을 계산할 수 있는 explicit 모델이다.

Pixel RNN

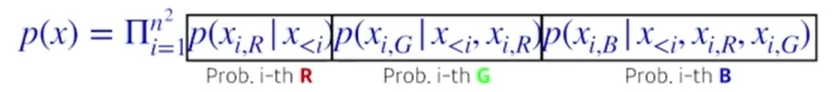
• pixel을 generate하기위해 RNN을 사용한 Auto-regressive Model

• odering을 어떻게 하느냐에 따라서 Row LSTM과 Diagonal BiLSTM으로 나뉜다.

본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.