Today I Learned

오늘부터 4주차. RecSys 기본 강의 수강을 시작한다.
오늘과 내일은 git 특강이 있어 그거부터 진행할 예정.

---

Git 특강

기본

• git을 쓰는 근본적인 이유? 버전관리를 통한 디버깅!

• vs code - ctrl+j : 밑에 터미널 창 단축키
  ctrl+, : 설정창

• 터미널에 bash 말고 딴거 있으면 기본프로필을 bash로 설정.
  터미널 스크롤은 위아래 화살표. 나가기는 q로 하면 된다.

• git 전역(global) 유저명 설정

git config --global user.name "유저명"
git config --global user.email "이메일"

• git log : 버전 확인. 지금까지 commit들 확인 가능.
  터미널이 보기 힘들면 git graph 확장프로그램 사용. 좌하단에 있다.
  git log는 head부터 부모 따라서 올라간다.
  gil log --all을하면 head부터가 아니라 모든 기록이 다 나온다.

• add는 변경사항을 commit 대기 상태로 만든다.

• 커밋id(식별자)는 name, content, email, message 등의 내용을 기반으로해서 sha-1로 해시해서 나온 해시값으로 사용한다.

• HEAD : 현재 보고있는 버전
  checkout : 원하는 다른 버전으로 head를 옮기는 것
  main : 돌아올 수 있는 원점.
  git checkout main : HEAD를 main으로 돌려보내는 코드
  detached HEAD state : 헤드가 main말고 다른 버전을 가르키는 상태.
  버리기 쉬우니 실험적인 기능을 구현할 때 사용하는 상태.

• head가 가르키고있는 버전이 이전 최신 버전이다.
  즉, 새로운 버전의 부모는 head다. 새로운 버전이 생기면 HEAD가 따라온다.
  즉, detached HEAD 상태면 main은 따라오지 않는다.

• 각각의 버전은 그 버전이 만들어진 시점의 staging area의 스냅샷이다.

• main이 exp 브랜치를 병합 : main에 HEAD가 있을 때 exp를 끌어와 병합
  실험이 끝났을 때

• exp가 main을 병합 : exp에 HEAD가 있을때 main을 끌어와 병합
  자주할수록 conflict가 줄어든다.

구조

in project folder

• Repository(.git)

• working directory : 실제 파일들이 있는 작업 공간
  HEAD와 같거나 커밋하지 않은 변경사항이 존재한다.

• staging area (index, cache)

---

강의 복습

최신 RecSys 동향

추천모델은 Shallow Model -> Deep Model -> Large-scale Generative Model로 발전하고있다.

• shallow model : 행렬을 분리해서 만드는 간단한 모델들

• Deep Model : Neural Networks를 사용하는 다수의 레이어를 가진 모델들

• Large-scale Generative Model : P5(추천 시스템을 언어 처리 문제로 접근), diffusion generative(diffusion 제거) 등의 모델을 사용한다.

• Explainability : 왜 그걸 추천한건지 설명을 하는 것

• Debiasing & Causality : 편향성을 제거하고(추천은 이미 데이터 자체가 대부분 편향적이라 이를 제거하는 것) 인과관계를 찾는 것.

통계학 기본

Random Variable(확률변수)

• 불확실한 사건의 결과를 수치로 나타낸 변수

• input은 sample space(가능한 모든 경우의 수), output은 실수 하나.

• 동전던지기에서 확률 변수 X는 앞면(X=1), 뒷면(X=0) 두가지 값을 가질 수 있다.
  P(X=1) = 0.5

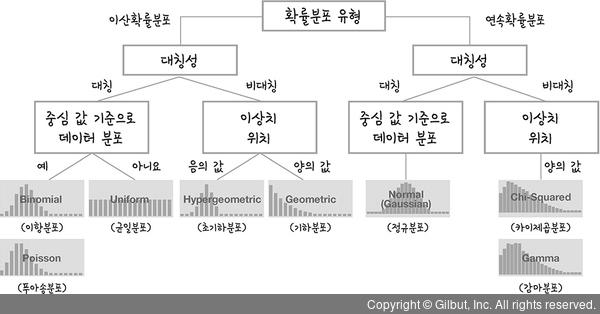
Distribution

이미지 출처 : @midoi327

• 확률변수의 가능한 값들이 어떻게 분포되어있는지 나타내는 함수

• 데이터 분포 패턴을 설명하고 특정 값이 나올 확률을 계산하는 데 사용된다.

• 크게보면 이산 확률 분포(discrete)와 연속 확률 분포(continuous)가 있다.

• 이항 분포 (Binominal Distribution)
  독립적이고 반복되는 n번의 실험에서 고정된 확률의 두 가지 결과를 따를 때 적용되는 분포
  동전 던지기, 성공-실패로 나눠지는 실험 등.
  베르누이 분포는 이항 분포 중에서 1번만 실험하는 경우다.

• 균등 분포(Uniform Distribution)
  모든 값이 동일한 확률로 나타나는 분포. 이산형, 연속형 다 가능하다.

• 가우시안 분포 (=정규분포)
  데이터가 특정 평균값 주변에 대칭적으로 분포되는 연속 확률 분포
  -무한~무한까지 값을 가진다. mean과 variance가 주어진다.

• 베타 확률 분포(Beta Distribution)
  0~1 사이의 값을 가지는 연속 확률 분포. 특정한 확률값을 모델링할 때 쓴다.
  알파와 베타 값에따라 그래프 모양이 달라진다.

중심 극한 정리(Central Limit Theorem, CLT)

무작위로 추출된 표본크기(sample size)가 커질수록 표본 평균의 분포는 모집단의 분포 모양과는 관계없이 정규분포에 가까워진다는 정리.

• 표본크기 = 각 실험에서 관측된 데이터의 개수

• 모수가 정규분포에서 나왔다면 표본의 평균($\bar{y}$)들의 분포가 정규분포를 따른다.

• 정규분포가 아니라도 표본 크기가 커진다면 모집단 분포와 상관없이 $\bar{y}$의 분포가 정규분포에 가까워진다.
  보통 n이 30이상이면 정규분포로의 근사가 잘 이루어진다고 본다.

Likelihood (우도)

주어진 데이터가 특정 모델과 파라미터 값 하에서 관측될 확률

• 확률은 모델이 주어졌을 때 데이터가 발생할 가능성을 측정.
  반면, 우도는 데이터가 주어졌을 때 모델이나 가설이 얼마나 그럴듯 한지 측정

• 결과 데이터가 특정 분포로부터 만들어졌을 확률

• 주로 파라미터 추정과 모델 선택에 사용된다.

• $L(\theta | x) = P(x|\theta) = \displaystyle\prod_{n=1}^N p(x_n|\theta)$. L이 likelihood, $\theta$는 모델 파라미터, x는 관찰된 데이터

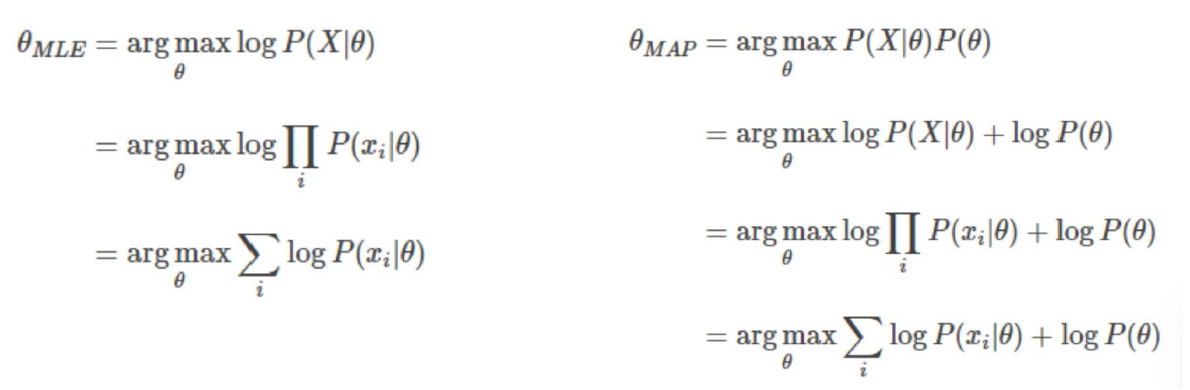
MLE (Maximum Likelihood Estimation,)

관찰된 데이터에 대해 likelihood를 최대화하는 파라미터를 찾는 방법
즉, 주어진 데이터를 가장 잘 설명하는 모델 파라미터를 찾는 것

• 수학적 계산을 더 쉽게 하기 위해서 로그 가능도를 사용한다.
  likelihood에 log와 -를 취해서 이 식을 미분해 0이되는 $\theta$값을 찾으면 그 값에서 로그가능도가 최소화가 되고, likelihood는 최대화가 되므로 해당 $\theta_{ML}$(파라미터)를 찾게 된다.

MAP(Maximum A Posteriori)

주어진 데이터에 대해 가장 높은 사후 확률을 가지는 모델 파라미터를 추정하는 방법

• Posterior(사후확률)을 최대로 하는 모수를 찾는 것

• $P(\theta | x) = \frac{P(x | \theta) \cdot P(\theta)}{P(x)}$ 베이즈 정리에 의거해서 사후확률 최대화는 likelihood * Prior를 최대로 한다는 것과 같다.(P(x)는 상수라 제외 가능)
  따라서 Prior를 알 수 있으면 사용할 수 있고, MLE와 동일하게 log를 사용해 최적화 한다.

---

피어세션

• 현업에서 github desktop, GUI버전도 많이 쓴다.

• 이번 주부터 통계위주의 수업이 많다. 배운내용 계속 복습하면서 remind 해야될 것 같다.

• 다음주 월요일까지 백준 코테 2문제!

---

회고

• 평소에 git을 자주 사용해서 알만한 내용은 다 안다고 생각했지만 이번 강의를 통해 HEAD에 대해 제대로 알게된 것 같아 좋았다.