Today I Learned

오늘은 다음주 월요일에 같이 리뷰할 Collaborative Filtering for Implicit Feedback Datasets 논문을 읽고 정리해봤다.

---

Collaborative Filtering for Implicit Feedback Datasets

• 논문 원문 링크

추천 시스템

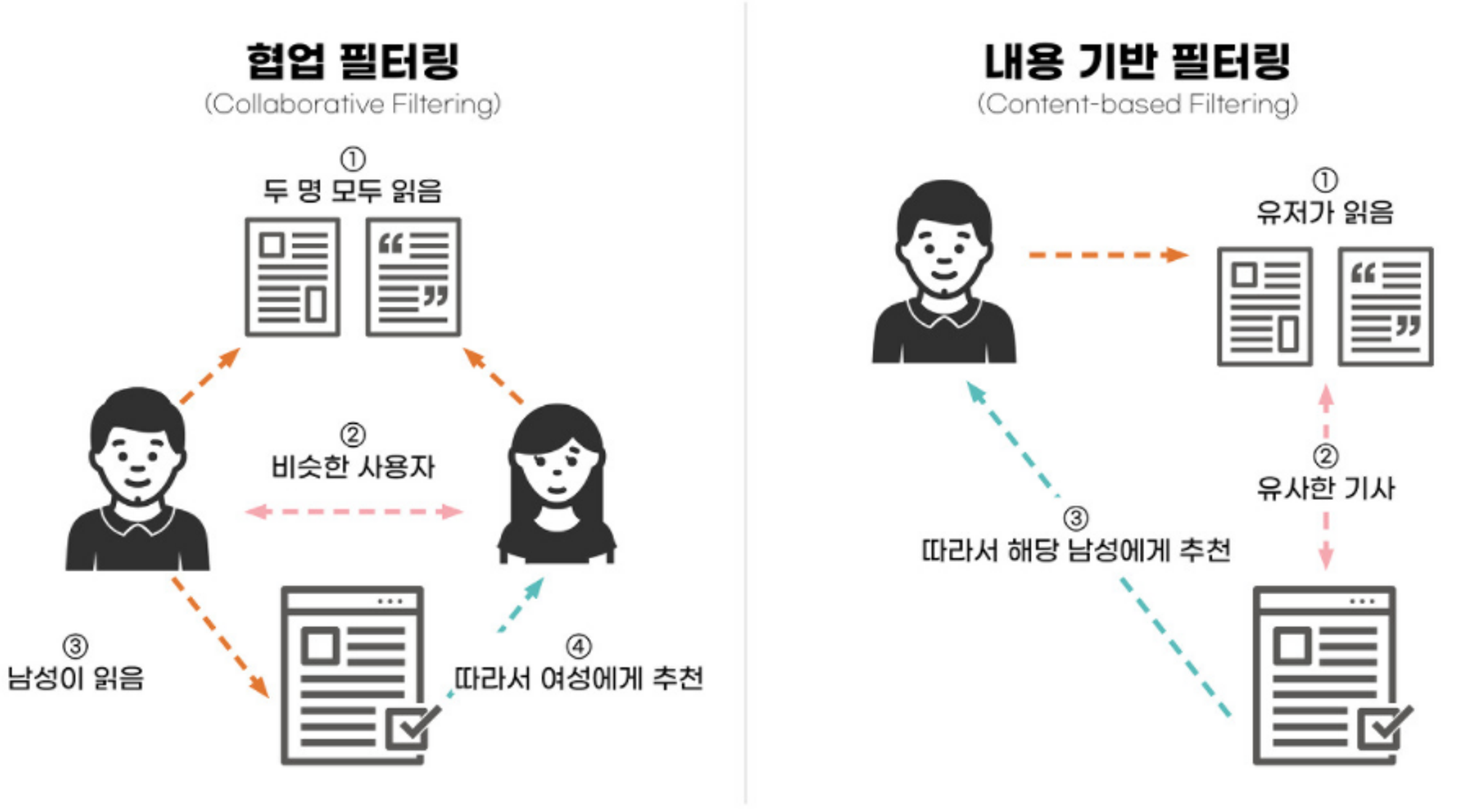이미지 출처 : daehong

Content-Based Filtering

유저가 과거에 좋아한 아이템의 특성을 분석해서 유사한 아이템을 추천하는 방식

• 유저나 제품에 대한 각각의 profile을 만들어 특성을 정의한다.(영화장르, 출연 배우 등)
• 생성된 profile을 기반으로, profile이 일치하는 제품을 추천한다.
• 주로 특성은 meta data.
• 새로운 사용자에게도 쉽게 적용할 수 있지만, 콘텐츠의 특성이 명확하게 드러나지 않으면 quality가 떨어질 수 있다.
• 유저의 content profile을 벗어나는 Overspecialization을 하기 힘들다.

Collaborative Filtering(CF)

유저의 행동을 바탕으로 다른 유저와의 유사성을 계산하고, 이를 기반으로 추천하는 방식

• 위의 방식처럼 명시적인 profile은 만들지 않고 상호작용 데이터만 사용한다.
• meta data가 필요없고 현업에서 많이 쌓이는 log 데이터로도 이용할 수 있다.
• 유저가 아이템에 가진 상호작용 특성을 행렬로 표현할 수 있다.
• 다양한 유저 데이터를 이용해 개인화된 추천을 제공할 수 있고 domain-free한 것이 장점이지만, 초기 데이터가 부족하거나 새로운 아이템의 경우 cold start 문제가 있다.
• 사용자 기반 : 취향이 비슷한 다른 유저가 좋아한 아이템 추천
• 아이템 기반 : 아이템간 유사도를 계산해 동일한 유저의 특정 아이템에 대한 예측 평점 계산
  아이템 기반이 확장성, 정확도, 설명력이 높다.
• 코사인 유사도 : 유사도 측정시 널리 쓰이는 방법. -1~1값을 가지며 유사한경우 $\theta$가 작아져 $\cos\theta$가 커진다.
  $similarity = \cos\theta = \dfrac{A\cdot B}{\|A\|\|B\|} = \dfrac{\sum A_iB_i}{\sqrt{\sum A_i^2}\sqrt{\sum B_i^2}}$

그 외

• 하이브리드 추천 시스템 : Content-Based Filtering + CF
• Deep Learning-Based : 신경망을 이용해 유저의 행동패턴이나 아이템의 특성을 학습해 추천.

---

논문 내용

implicit feedback(암시적 피드백)

명시적 피드백(Explicit Feedback)처럼 유저가 직접 평가나 선호도를 표현(별점, 리뷰)하지 않았지만, 행동을 통해 유추할 수 있는 피드백
ex)구매 이력, 검색패턴, 클릭 횟수, 체류 시간, 재시청여부, 마우스 움직임 등

• 부정적(negative) 피드백이 없다. 유저의 행동을 통해 어떤걸 좋아할지는 알아도 어떤걸 싫어하는지는 신뢰성 있게 추정하기 어렵다. 그렇다고 해서 알 수 있는 정보에만 치중하면 긍정적 피드백만 남아 유저 선호도를 왜곡할 수 있다.

• 유저 데이터 수집에 동의만 하면, 대규모 데이터를 수집할 수 있고, 유저의 실제 행동을 반영하고, 유저가 추가적인 노력을 하지 않아도 된다. 하지만 노이즈가 많고, 해석이 어렵다.

• 명시적 피드백의 숫자(점수)는 선호(preference)를 나타내지만, 암시적 피드백에서 숫자(빈도)는 높다고해서 반드시 선호로 이어지지는 않는다. 다만 신뢰도(confidence)로 볼 수 있다.

---

기존 방식들

• Neighborhood models
  아이템 중심의 CF. 명시적 피드백을 다룰 땐 잘 적용되고, 추천에 대한 설명을 할 수 있는게 장점
  아이템간의 유사성 측정은 피어슨 상관계수로.
  $r_{ui}$는 비슷한 k개 아이템에 대한 유저 u의 가중평균으로 계산.
  암시적 피드백에 대해 preference와 confidence를 구분할 수 없는게 문제.

• Latent Factor Models
  잠재 요인을 만들고 이를 이용해서 계산.
  SVD모델(행렬 분해)을 이용해서 유저 벡터와 아이템 벡터의 내적을 이용해 예측.
  +정규화+SGD를 이용해 파라미터 구함. 추천에 대한 설명을 할 수 없는게 단점
  이 모델에서 $r_{ui}$는 explicit feedback만 사용한다.
  논문에서는 이 모델을 수정해 암시적 피드백을 적용하려 함.

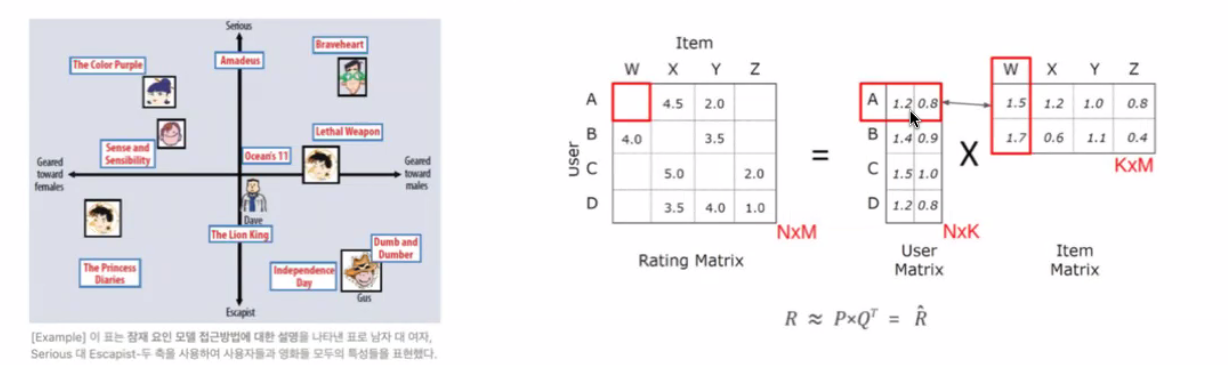
rating matrix를 latent user / item factor로 분해한다.
유저(n)와 아이템(m)을 같은 k차원으로 보낸 것
k는 의미를 설명하기 힘든 latent 요소다.

논문 모델

• $p_{ui}$ : 선호도. u가 i를 선호하는지 나타내는 이진 변수.
  $r_{ui}$가 0이면 0 / 0이상(유저가 아이템을 소비했으면)이면 1.
  기법에 따라 수정 가능.

• $c_{ui} = 1 + \alpha \cdot r_{ui}$ : 신뢰도 변수.
  앞에 1을 붙이는 이유는 뒤의 $C^u-I$ 계산에서 1을 빼서 $r_{ui}$가 0인걸 제외하기 위함.
  $r_{ui}$가 클수록 파라미터(알파)에 따라 신뢰도가 증가한다.(40일때 결과가 좋았다)
  기법에 따라 $c_{ui} = 1 + \alpha \cdot log(1+r_{ui}/\epsilon)$도 사용

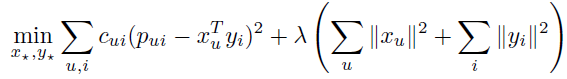
• 비용함수
  앞쪽은 사용자의 선호도와 모델의 예측값(유저-아이템 벡터의 내적)을 오차로 보고 오차를 제곱해 신뢰도 가중치를 곱해 모든 유저-아이템쌍을 합한 것이고,
  뒤는 overfit을 막기위해 유저, 아이템 벡터 크기를 제한하는 정규화 항으로 유저,아이템 벡터의 L2노름의 제곱합이다. λ값은 정규화 강도를 조절하는 하이퍼 파라미터다.

• Alternating Least Squares: ALS, 교차 최소 제곱. 행렬 분해 문제의 최적화 알고리즘
  유저-아이템 상호작용 행렬을 두개의 저차원 행렬의 곱으로 근사하고, 하나를 고정하면 비용함수는 convex 함수가 되어 SGD로 전역 최소값을 쉽게 값을 구할 수 있다. 둘을 교대로 고정하면서 재계산해 비용함수의 값을 줄인다.

• u와i 2가지를 가져 매우 고차원이라 계산이 복잡하고 길어지므로 최적화를 하는 것이다.
  계산 방식은 thelazyday 블로그 참고.

• 비용함수를 최소화하는 $x_u$, $y_i$를 찾는 과정에서 계산적 병목은 $Y^TC^uY$에서 발생하는데 이는 $Y^TY + Y^T(C^u-I)Y$로 구할 수 있고, n에는 zero-element도 있으므로, 결과적으로 $x_u$는 $O(f^2N+f^3m)$으로 구할 수 있는데 f(=factor)는 일반적으로 20~200개를 사용하니 상수 취급하면 input size n에 대해 선형 시간복잡도로 결과를 구할 수 있다. 이는 $y_i$에도 적용된다.

• 기법에 따라 차이는 있지만 중요한 것은 raw observation($r_{ui}$)를 쓰지않고 $p_{ui}$와 $c_{ui}$ 두 개념으로 나눠서 해석해야한다는 것과 모든 유저와 아이템에 대해 선형 시간 복잡도를 유지하기 위해 대수적 구조를 이용해 계산을 최적화해야된다는 것이 핵심이다.

• Explaining
  좋은 추천은 설명이 동반되어야 한다. Neighborhood는 설명이 쉬우나 Latent Factor 모델은 어렵다. 사용자 행동이 잠재요인으로 추상화되어 직접적인 관계를 설명하기 어렵기 때문이다.
  하지만 논문 모델은 ALS를 사용해서 아래와 같이 u의 i에 대한 예측 선호도를 가중치가 적용된 선형 모델로 나타낼 수 있다. 과거 행동 각각이 추천에 미치는 영향을 개별적으로 평가할 수 있어, 추천을 명확하게 설명할 수 있어진다.
  

---

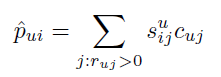
실험

• 4주간 train, 1주간 test. 셋톱박스 30만개, 방송 프로그램 17000개. $r_{ui}$ 약 3200만.
  매주 반복해서 보는 프로그램은 쉬우므로 예측에서 제외. $r_{ui}^t < 0.5$는 0으로 설정.

• 모멘텀 효과 고려해서 채널 바꾸고 2번째 프로그램부터는 가중치를 줄인다.
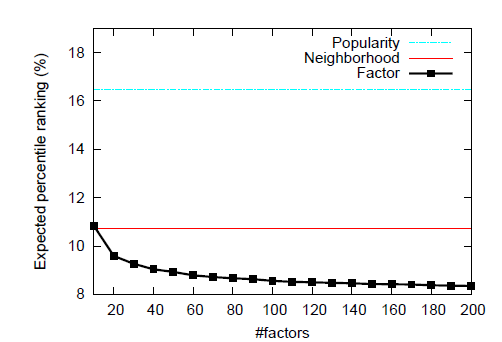
  $rank_{ui}$는 0%(가장선호)~100%의 백분위로 표현한다.(무작위 예측 시 50%)

• 인기 기반 추천, neighborhood 2가지를 경쟁모델로 놓고 논문 모델과 실험.
  rank 결과는 아래와 같이 논문 모델이 우월하다. factor를 많이 쓸 수록 개선됐다.
  누적 분포 함수로 볼 때는 rank 1%가 약 27%로 논문 모델이 더 결과가 좋았다.
  

• λ=150으로 정규화했을때 결과가 가장 좋았고, 정규화하지 않을 경우 다른 모델들보다 오히려 성능이 좋지 않았다.

• 인기 있는 프로그램은 더 예측하기 쉬웠지만, 유저의 시청시간은 크게 중요한 요소가 아니었다.

• neighborhood 모델과 유사하게 상식적인 선에서 비슷한 프로그램들로 추천한 이유를 설명할 수 있다.

---

결론

• 암시적 피드백 데이터셋에서 유저와 아이템의 관계는 preference(선호도)와 confidence(신뢰도)를 별도로 고려하는 것이 매우 유용하다.

• missing data를 포함해 모든 유저-아이템 선호도를 input으로 활용하는 것은 확장성에 문제가 될 수 있지만, 이 모델에서는 algebraic structure(대수적 구조)를 이용해 모든 데이터를 이용하면서도 선형 시간 복잡도로 작동되는 알고리즘으로 해결했다.

• 이 모델은 기존 Latent Factor 모델에서는 할 수 없었던 추천에 대한 설명을 할 수 있게되어 유저가 추천시스템을 더 잘 이해할 수 있게 해준다.

• zero preference 상황에서 어떻게 confidence를 나눌지에 대해 추가적인 연구가 필요하다.

---

멘토님 코멘트

• 현업에서도 아직 많이 쓰이고, netflix에서도 실제로 쓰였던 모델. 행렬 기반모델로 성능이 아주 좋다.