
Sptial filter (공간 필터)
spatial filter는 이미지의 각 픽셀과 이웃하는 픽셀에 대하여 수행하는 연산을 말한다. 공간 필터링은 이미지의 공간 영역에서 직접 적용되며, 픽셀값을 변형하여 이미지를 변환한다. 주로 특징 추출이나 노이즈 제거에 활용된다.
공간 필터는 일반적으로 커널(kernel)과 연산(operation)으로 구성된다. 커널은 공간 필터의 가중치를 담고 있는 행렬로, 커널의 크기는 공간 필터의 크기를 결정한다. 연산은 근방 픽셀에 커널에서 정의된 연산(가중 평균 등)을 수행한다.
대표적인 공간 필터에는 smoothing filter(평활화 필터), edge detection filter(엣지 검출 필터), morphological operation filter(모폴로지 연산 필터)가 있다.
Low-pass filter(LPF), High-pass filter(HPF)
Low-pass filter(저역 통과 필터)
저주파 신호는 통과시키고, 고주파 신호를 차단하는 필터이다. (고주파수 성분은 이미지 세부사항, 노이즈와 같은 부분) 영상처리에서 저역 통과 필터는 세밀한 부분(noise, edge 등)을 흐리게 하거나 제거하여 이미지를 부드럽게 만드는 데 사용된다.
→ 스무딩 필터는 여기에 속한다고 볼 수 있다.
e.g. Gaussian filter, mean filter, …
High-pass filter(고역 통과 필터)
고주파 신호는 통과시키고, 저주파 신호를 차단하는 필터이다. (저주파수 성분은 부드러운 변화, 큰 형태 같은 부분) 영상처리에서 고역 통과 필터는 세밀한 부분을 강조하고, 전체적인 밝기 변화가 적은 부분을 억제한다. 주로 edge 검출, 세부 텍스쳐 강조에 사용된다.
→ 엣지 검출 필터는 여기에 속한다고 볼 수 있다.
e.g. sobel filter, laplacian filter, …
Smoothing Filters
스무딩 필터(smoothing filter)는 영상의 잡음을 줄이고 세부사항을 부드럽게 만든다. 스무딩 필터의 종류는 다양하지만, 여기서는 가우시안 스무딩을 위주로 다루려고 한다.
Mean filtering (Box filter)
mean filter는 단순하고 직관적인 스무딩 방법으로, 인접한 픽셀들의 평균값을 구하여 각 픽셀값을 대체시킴으로써 대표성이 없는 픽셀값을 제거할 수 있다. mean filtering은 컨볼루션 필터로, mean filter의 커널(kernel)은 다른 컨볼루션과 같이 평균을 계산할 때 샘플링하고자 하는 이웃의 형태와 크기를 나타낸다.
일반적으로 3*3 정사각형 형태의 커널이 사용되며, 더 큰 크기의 커널을 사용하면 스무딩의 강도가 높아진다.
Gaussian smoothing
Gaussian smoothing의 basic idea는 컨볼루션(convolution)을 통해 point-spread function(PSF, 점 확산 함수)처럼 2D 가우시안 분포를 사용하는 것이다. 이미지는 이산(discrete) 픽셀들의 집합으로 구성되어 있기 때문에, 컨볼루션을 수행하기 전 가우시안 함수를 통하여 근사한 이산값을 생성해야 한다.
이론적으로 가우시안 분포는 전 지점에서 0이 아닌 값을 갖지만, 실제로 평균에서 약 3이상 떨어진 값은 0으로 취급하는 것이 효율적이다. 따라서 우리는 이 점에서 커널을 잘라낼 수 있다.
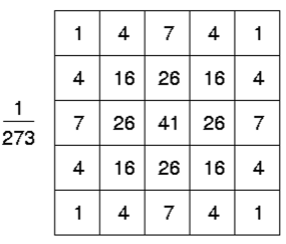
위 커널은 가우시안 함수를 통해 이산화된 2차원 분포로, 5x5 가우시안 커널의 한 예시이다. 커널의 각 요소는 가우시안 함수를 통해 계산된 가중치를 나타내며, 이미지에 이 커널을 합성곱하면 스무딩이 적용된다. 커널은 이미지의 중심점 주변 픽셀에 더 큰 가중치를 두고, 주변 픽셀의 가중치는 점점 감소시킨다.
커널 내 모든 값을 더하면 273이 되고, 따라서 커널 전체에 1/273을 곱하여 정규화하는 과정을 거친다. 이는 커널 적용 후에도 이미지의 밝기가 유지되도록 하기 위함이다. 정규화된 가우시안 커널은 가 1.0인 가우시안 함수를 근사화한다.
2차원 그레이스케일 이미지에서 가우시안 필터를 적용한다고 할 때, 가우시안 함수 식은 다음과 같다. (joint Gaussian pdf와 동일한 형태이다)
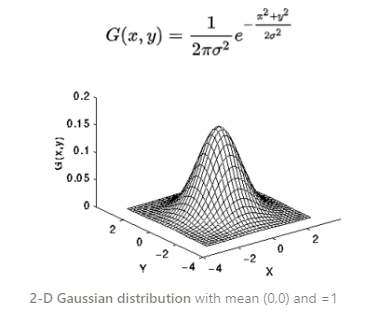
Mean filter vs Gaussian filter
Gaussian smoothing의 적용 효과는 mean filter와 유사하다. 스무딩의 강도는 Gaussian의 표준편차 값에 따라 조정된다. (표준편차 값이 클수록 강한 스무딩 효과)
가우시안은 각 인접 픽셀의 가중 평균(weighted average)을 출력하는데, 중심 픽셀으로 갈수록 더 많은 가중치가 부여된다. 반면, mean filter는 모든 픽셀에 균일한 가중 평균이 부여된다. 이로써 Gaussian filter가 동일한 크기의 mean filter보다 엣지를 더 잘 보존할 수 있게 된다.
가우시안을 스무딩 필터로 사용하는 이유 중 하나는 주파수 응답(frequency response) 때문이다. 대부분의 컨볼루션 기반 스무딩 필터는 low-pass frequency filter인데, low-pass filter는 high spatial frequency 성분을 제거한다. 가우시안의 퓨리에 변환(Fourier Transform)도 역시 가우시안이기 때문에, 가우시안 블러를 적용하면 이미지의 고주파 성분을 줄이는 효과가 있다.
mean filter와 gaussian filter는 모두 고주파수 성분을 감소시키지만, mean filter는 주파수 응답에서 oscillation(진동)이 발생한다. 반면, gaussian filter는 진동이 발생하지 않는다. 실제로, 주파수 응답의 곡선 자체가 half gaussian 형태이다. 따라서, 적절한 크기의 Gaussian filter를 선택하면 필터링 후 이미지에 어떤 주파수 성분이 포함되어 있는지 예측하기가 더 쉽다.
Gaussian Smoothing Application
opencv에서 GaussianBlur를 사용하면 간편하지만, 여기서는 가우시안 스무딩이 적용되는 과정을 좀더 자세히 살펴보자.
# 1. 1차원 가우시안 커널 생성
gk = cv2.getGaussianKernel(5, -1, cv2.CV_64F)
# 2. x커널, y커널을 외적하여 2D 가우시안 커널 생성
gaussian_kernel_2d = np.outer(gk, gk.T)
# 3. 가우시안 커널에 이미지를 컨볼루션하여 결과 생성
dst = cv2.filter2D(gray, -1, gaussian_kernel)
dst
cv2.getGaussianKernel()은 커널의 크기와 를 지정하면, 1D 가우시안 커널을 생성한다. 여기서는 5*5 Gaussian filter를 적용하기 위해 ksize=5의 커널을 생성했다.
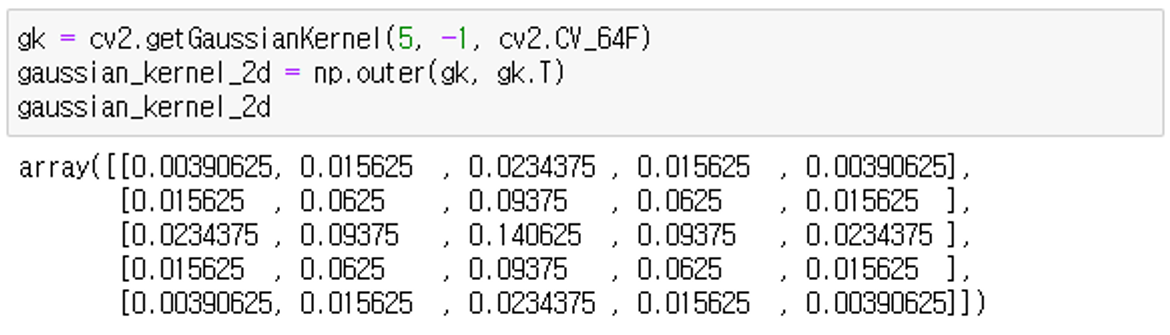
이미지를 필터링하기 위해서는 2D Kernel이 필요하므로, 앞서 만든 가우시안 커널을 전치(Transpose)한 다음 두 X,Y 커널을 외적하여 2D 가우시안 커널을 만든다.
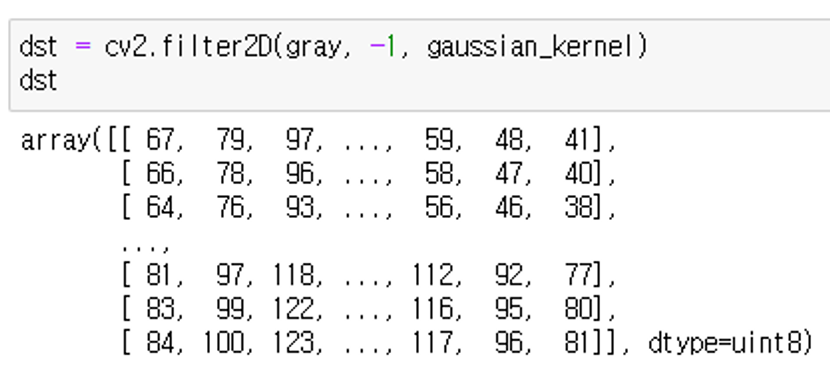
마지막으로 원본 이미지에 Gaussian kernel을 컨볼루션 연산하게 되면 가우시안 블러가 적용된 결과물을 얻을 수 있다.
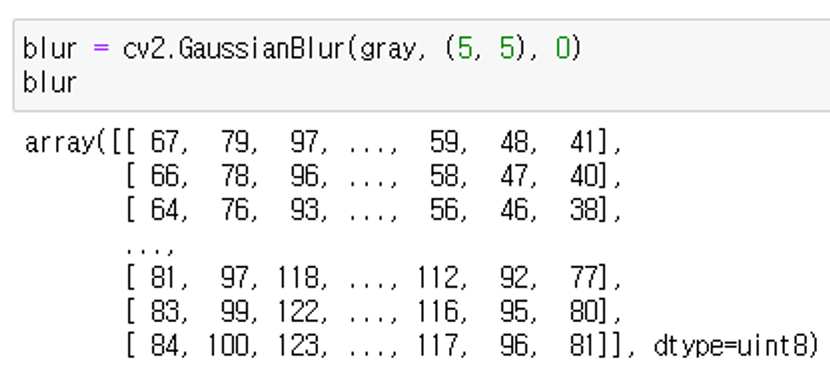
이미지에 cv2.GaussianBlur를 적용해 보면 직접 커널을 만들고 컨볼루션 연산을 수행했을 때와 값이 같은 것을 확인할 수 있다.
스무딩 적용 전, 후를 비교해보면 5*5 커널 기준이라 그런지 육안으로 큰 차이는 보이지 않는다. (샘플을 잘 못 고르기도 한 것 같다 ^^;;)
하지만 가우시안 스무딩은 lowpass filter이므로, 스무딩 적용 후에 고주파 성분들이 제거되었을 것이다. 그렇다면 제거된 고주파 성분을 한번 확인해보자.
lpc = cv2.GaussianBlur(gray, (5, 5), 0)
hpc = cv2.subtract(gray, lpc)
plt.imshow(hpc, cmap='gray')
plt.axis('off')원본 이미지에서 가우시안 블러를 적용한 후, 원본 이미지와 블러가 적용된 이미지의 차이를 연산(cv2.subtract)하면, 제거된 고주파 성분들이 검출된다.

시각화 해 보면, 뚜렷하진 않지만 춘식이 이미지의 엣지 부분이 검출된것을 확인할 수 있었다. (착한사람만 보임.. )
추가로, 가우시안 커널의 크기를 21*21로 늘려보면 아래와 같이 고주파 성분들이 더 잘 검출된다.

