Optical Flow(광학 흐름)와 Lucas-Kanade method

Optical Flow

Optical flow는 연속된 프레임 간 픽셀 이동을 관찰하고, 이를 통해 움직임의 방향 및 속도를 파악한다.

Optical flow는 다음 2가지 가정 하에 작동한다 :

1. 연속하는 프레임 간 픽셀 강도(intensity)는 변하지 않는다.
2. 인접 픽셀은 유사한 움직임을 갖는다.

첫 프레임에서의 픽셀 $I(x, y, t)$이 $dt$ 시간 이후 다음 프레임에서 $(dx, dy)$ 만큼 움직였다고 한다면, 그리고 위 가정을 적용하여 픽셀의 강도가 변하지 않는다면, 다음과 같은 식을 세울 수 있다.

$I(x,y,t)=I(x+dx,y+dy,t+dt)$

그리고 우변에 테일러 급수(Taylor Series)를 취한 후, 공통 항을 제거하고 $dt$로 나누면 다음과 같은 식이 도출된다.

$f_xu+f_yv+f_t=0$

여기서 $f_x=\frac{∂f}{∂x}$; $f_y=\frac{∂f}{∂y}$ , $u=\frac{dx}{dt}$ ;$v=\frac{dy}{dt}$ 이며, 위 식을 Optical Flow equation이라 한다. $f_x$와 $f_y$는 이미지의 그래디언트이고, $f_t$는 시간에 따른 그래디언트이다.

테일러 급수(Tayler Series) [참조]
여러 번 미분가능한 함수 $f(x)$에 대하여 $x=a$에서 $f(x)$에 접하는 “멱급수”로 표현하는 방법

광학 흐름 방정식에서 이 $u, v$는 알려지지 않은 변수인데, 이를 풀기 위한 다양한 알고리즘이 제시되었다.

그 알고리즘들에는 대표적으로 Lucas–Kanade, Horn-Schunck, Buxton-Buxton 등이 있다. 본 포스팅에서는 Lucas–Kanade method에 대해서만 다루려고 한다.

---

Lucas-Kanade Method

Lucas-kanade는 널리 사용되는 광학적 흐름 추정 방법으로, 픽셀의 일정 이웃 영역(local neighbor) 내(예를 들면 5x5 영역)에서의 흐름은 constant하다고 가정하고, 이 이웃 내 모든 픽셀의 기본 광학 흐름 방정식을 최소제곱법(Least squares)을 사용하여 해결한다.

Lucas-kanade 방법은 인접 픽셀의 정보를 결합하여 광학적 흐름 방정식을 해결할 수 있도록 한다. 이 방법은 point-wise method에 비해 노이즈에 덜 민감하다는 장점이 있다. 한편, 순수하게 local 기반으로 흐름을 계산하기 때문에 균일한 영역의 내부에 대한 흐름 정보를 얻기 어렵다는 단점이 있다.

Concept

Lucas-kanade는 두 프레임 간 픽셀의 이동이 작고 점 $p$ 주변 이웃 내에서 일정하다고 가정하며, p에 중심을 둔 window 내 픽셀에 대한 국소 이미지 흐름 벡터 $(V_x, V_y)$는 다음을 만족하여야 한다.

$I_x(q_1)V_x + I_y(q_1)V_y = - I_t(q_1)$

$I_x(q_2)V_x + I_y(q_2)V_y = - I_t(q_2)$

…

$I_x(q_n)V_x + I_y(q_n)V_y = - I_t(q_n)$

여기서 $q_1, q_2, …, q_n$은 window 내부 픽셀을 나타내고, $I_x(q_i), I_y(q_i), I_t(qi)$는 이미지 $I$의 $x, y$ 위치와 시간 $t$에 대한 편미분(partial derivatives)으로, 점 $q_i$와 현재 시간으로 계산된다.

이러한 방정식은 $Av=b$ 형식의 행렬로 표현할 수 있다.

5x5 window를 사용했을 때 matrix form

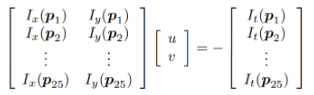
이 시스템은 미지수보다 더 많은 방정식을 가지므로, 일반적으로 과결정(overdetermined)상태이다. Lucas-Kanade 방법은 최소제곱법을 사용하여 타협적인 해를 찾는다.

즉, $2\times 2$ 시스템을 해결하여

$A^TAv = A^Tb$ 또는 $v = (A^TA)^{-1}A^Tb$

이 방정식에서 중앙 행렬은 역행렬로, 합계는 $i=1$에서 $n$까지 수행된다. $A^TA$ 행렬은 점 p에서 구조 텐서(structure tensor)라고도 한다.

$A^TAv = A^Tb$ 를 해결하기 위한 가정

• $A^TA$ 행렬이 가역(invertible)행렬
• $λ_2$가 너무 작아선 안 됨 (잡음 이슈). $λ_1$$/$ $λ_2$가 너무 크면 aperture problem이 발생할 수 있음

---

Implement code

Lucas-Kanade method를 사용하여 광학 흐름을 구현하여 보자.

import cv2
import numpy as np

cap = cv2.VideoCapture('./data/walking.avi')

# ShiTomasi 코너 검출기의 매개변수
feature_params = dict(maxCorners=100,
                      qualityLevel=0.3,
                      minDistance=7,
                      blockSize=7)

# Lucas-Kanade 광학 흐름 매개변수
lk_params = dict(winSize=(15, 15),
                 maxLevel=2,
                 criteria=(cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))

# 임의의 색상 생성
color = np.random.randint(0, 255, (100, 3))

# 첫 프레임과 그레이 스케일 변환
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)

# 마스크 이미지 생성
mask = np.zeros_like(old_frame)

while True:
    ret, frame = cap.read()
    if not ret:
        break
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

    # 광학 흐름 계산
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)

    # 좋은 특징점 선택
    good_new = p1[st == 1]
    good_old = p0[st == 1]

    # 특징점 추적 시각화
    for i, (new, old) in enumerate(zip(good_new, good_old)):
        a, b = new.ravel()
        c, d = old.ravel()
        a, b, c, d = int(a), int(b), int(c), int(d)
        mask = cv2.line(mask, (a, b), (c, d), color[i].tolist(), 2)
        frame = cv2.circle(frame, (a, b), 5, color[i].tolist(), -1)
    img = cv2.add(frame, mask)

    cv2.imshow('frame', img)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break

    # 다음 반복을 위해 현재 프레임과 포인트 업데이트
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)

cv2.destroyAllWindows()
cap.release()

---

References

OpenCV: Optical Flow
Lucas–Kanade method(wikipedia)
Lucas-Kanade Optical Flow(Carnegie Mellon University)