manifold learning : Autoencoders

Manifold Learning

manifold learning은 고차원 데이터 학습 시 발생하는 차원의 저주(curse of dimensionality)를 극복하기 위해 고안된 접근법으로, “고차원 데이터가 사실상 저차원 공간(manifold)에 놓여있다”는 가정(manifold hypothesis)에서 출발한다. 데이터를 더 낮은 차원으로 변환하면서, 데이터의 핵심 구조와 특성을 유지하는 것이 학습 목표다.

• Manifold Hypothesis

  데이터가 고차원 공간에 존재하더라도, 실제로 의미 있는 데이터 분포는 더 낮은 차원의 매니폴드에 집중되어 있다. 예를 들어, 얼굴 이미지는 수백만 픽셀의 고차원 공간에 있지만, 실제 다양한 얼굴의 특징들은 훨씬 적은 차원으로 표현될 수 있다.
  

• Curse of Dimensionality

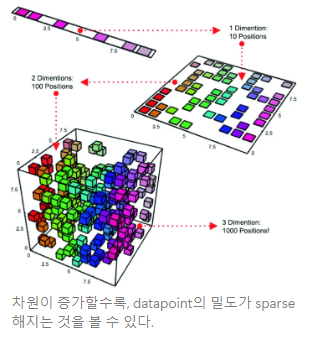
  데이터 차원이 증가할수록, 분포하는 데이터 포인트의 밀도가 sparse해진다. 차원을 증가시키면서 데이터 밀도를 유지하려면 훨씬 더 많은 데이터 수가 필요하며, 적은 데이터로 학습하게 되면 학습 모델이 제대로 일반화하지 못하고 overfitting이 발생하기 쉽다. (적은 데이터로 고차원 공간을 표현하기 어렵다)
  또한, 데이터 차원이 증가할수록 요구하는 계산량 또한 기하급수적으로 증가한다.

  → manifold learning을 통해 차원을 축소하고, 이러한 위험성을 피하자! 는 것이 basic concept이다.
  

이러한 학습 기법은 dimensionality reduction(차원 축소)이라고도 하며, 차원 축소 기법에는 Linear, Non-linear 방식으로 나눌 수 있다.

• Linear method : PCA(Principal Component Analysis), LDA(Linear Discriminant Analysis), MDS(Metric Multidimensional Scaling), ..

• Non-linear method : t-SNE(t-Distributed Stochastic Neighbor Embedding), Isomap, LLE(Locally Linear Embedding), UMAP(Uniform Manifold Approximation and Projection), Auto-Encoder, ..

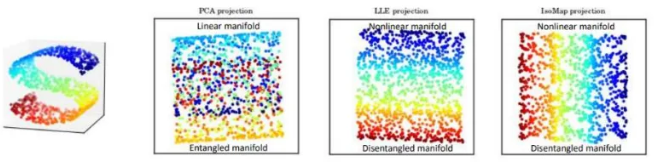
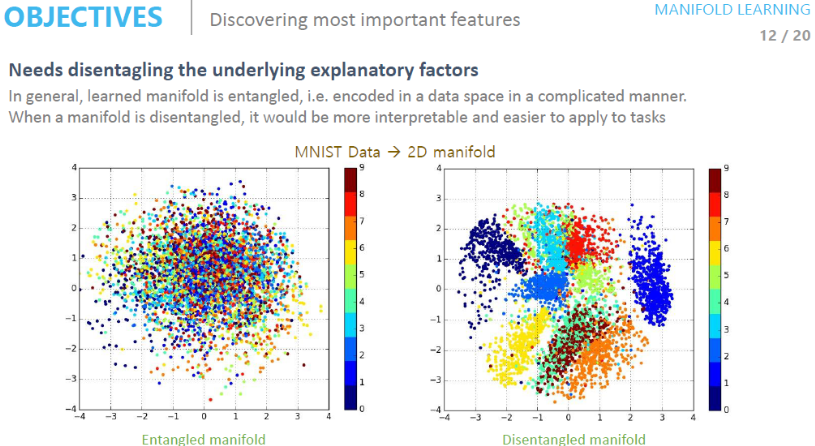
• Disentangled Manifold

  차원 데이터의 잠재 공간(latent space)을 구성하는 각 변수(latent variable)가 독립적이고 의미 있는 속성을 표현하도록 학습하는 방법. 이를 통해 데이터를 해석하고, 조작하고, 새로운 데이터를 생성할 수 있다.
  

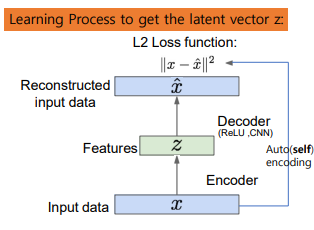
AutoEncoder

AutoEncoder는 앞에서 설명한 non-linear dimensionality reduction 기법으로, Encoder-Decoder 구조를 통해 입력 데이터를 압축하고, 재구성(reconstruction)하는 방식으로 데이터의 잠재 특성을 학습하는 모델이다.

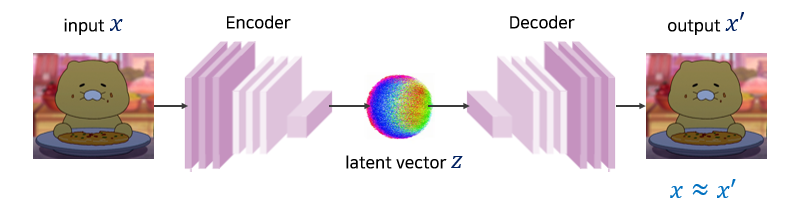
Autoencoder의 구조

• Encoder : 고차원 데이터 $x$를 입력받아 저차원의 latent space로 압축. $h=σ(Wx+b)$ 이 때, $h$는 학습하고자 하는 latent vector ($z$)
  

• Latent Space (Bottleneck) : 입력 데이터의 압축 표현(latent representation)이 만들어지는 지점으로, 정보 손실을 최소화하면서 데이터의 본질적 특징을 포착한다.
  

• Decoder : 잠재 공간의 데이터를 원래 입력 데이터 공간으로 복원(reconstruct). $x' =ϕ(W^Th+b)$
  

Training Objectives

autoencoder의 loss function은 input data $x$와 reconstructed data $x'$ 간 차이를 최소화하는 방식으로 학습한다. 일반적으로 MSE Loss를 사용.

$\mathcal{L}_{MSE}=\frac{1}{N}∑∥x_i−x'_i∥^2$