로지스틱 회귀분석(Logistic Regression) 정복하기

정예슬·2022년 7월 21일

로지스틱 회귀

machine learning

목록 보기

4/4

오늘은 로지스틱 회귀의 개념과 python을 활용한 실제 분석 과정을 정리하고자 한다.

Logistic Regression

Y 값이 범주일 때 수행하는 분석 기법으로, X 변수를 로지스틱 함수 형태(비선형결합)로 표현하고, 관측치가 특정 범주에 속할 확률로 계산한다.

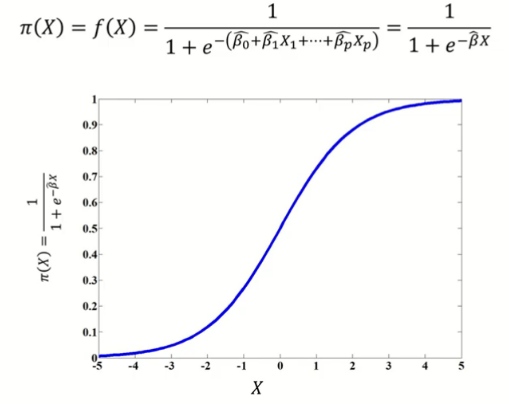
Maximum Likelihood Estimation(최대 우도 추정법)

로지스틱 회귀는 로그 우도함수(log likelihood function)가 최대가 되는 파라미터 $\beta$ 를 결정하는 과정이다.
확률 함수 $f_i(y_i) = \pi(x_i)^{y_i}(1-\pi(x_i))^{1-y_i}$ 에 로짓 변환을 수행하여 식 $\sum_i y_i (\beta_0 + \beta_1X_1 + ... + \beta_pX_p) - \sum_i ln(1+e^{\beta_0+\beta_1X_1+...+\beta_pX_p})$ 을 도출한다.

log likelihood function 도출 과정

$L =\prod_{i}^{n}f_i(y_i) = \prod_{i}^{n}\pi(x_i)^{y_i}(1-\pi(x_i))^{1-y_i}$

ln $L = ln \left [\prod_{i}(x_i)^{y_i}(1-\pi(x_i))^{1-y_i} \right]$

$ln \prod_i\left[{\pi(x_i)\over 1-\pi(x_i)} \right]^{y_i} + \sum_i ln(1-pi(x_i))$

$= \sum_i y_i ln \left[ \pi(x_i)\over 1-\pi(x_i) \right] + \sum_i ln(1-\pi(x_i))$

(로짓 변환) $= \sum_i y_i (\beta_0 + \beta_1X_1 + ... + \beta_pX_p) - \sum_i ln(1+e^{\beta_0+\beta_1X_1+...+\beta_pX_p})$

로그 우도함수는 파라미터 $\beta$ 에 대하여 비선형이므로, 선형 회귀 모델과 같이 명시적인 해가 존재하지 않는다.

Cross Entropy(교차 엔트로피)

교차 엔트로피는 두 확률 $p(x)$ 와 $q(x)$ 간 차이를 나타낸다.

$Cross Entropy = - \sum p(x) \log q(x)$

교차 엔트로피는 음의 로그 우도 함수 기댓값과 같다.
로그 우도 함수를 최대로 하는 것은, 입력 분포 $p(x)$ 와 파라미터가 주어졌을 때, 출력 분포 $q(x)$ 의 확률을 최대로 하는 것과 같다.
교차 엔트로피를 최소로 하는 것은, 입력 분포 $p(x)$ 와 출력 분포 $q(x)$ 의 차이를 최소로 하는 것과 같다.

결국 로지스틱 함수의 최적 파라미터는 로그 우도 함수를 최대로, 즉 교차 엔트로피를 최소로 하는 것이다.

Odds Rate(승산비)

선형 회귀 모델을 해석할 때는, 입력 변수가 1단위 증가할 때 출력변수의 변화량으로 해석한다.

$f(X) = \widehat{\beta_0} + \widehat{\beta_1X_1} + ... + \widehat{\beta_pX_p}$

반면 로지스틱 회귀 모델을 해석할 때는, 입력변수가 1단위 증가할 때 log Odds(로그 오즈)의 변화량으로 해석한다.

$\log(Odds) = \widehat{\beta_0} + \widehat{\beta_1X_1} + ... + \widehat{\beta_pX_p}$

승산비란, 나머지 입력 변수가 모두 고정된 상태에서 한 변수를 1단위 증가시켰을 때 변화하는 Odds의 비율이다.

${odds(x_1+1, x_2, …, x_n) \over odds(x_1, x_2, …,x_n)} = {e^{\widehat{\beta_0} + \widehat{\beta_1}(X_1+1)+...+\widehat{\beta_p}X_p}\over {\widehat{\beta_0} + \widehat{\beta_1}X_1+...+\widehat{\beta_p}X_p} } = e^{\beta_1}$

$x_1$ 이 1단위 증가하면, 성공에 대한 승산비가 $e^{\beta_1}$ 만큼 변화하며, coefficient(회귀 계수)가 양수이면 성공 확률이 증가하고(성공 확률 >= 1), 음수이면 성공 확률이 감소한다 (0<=성공확률<1).

로지스틱 회귀 분석 과정

먼저 로지스틱 회귀 분석을 적용하고자 하는 데이터를 준비한다. 나는 내가 분석하고자 하는 데이터를 전처리해서 준비해 뒀다. 내가 사용한 데이터는 종속 변수가 0과 1로 분류되는 이진 분류 유형 데이터이다.

분석에 필요한 친구는 statsmodel API라는 훌륭한 모듈이다(그리고 해석할 능지). 회귀계수, p-value, std error 등등 변수만 넣으면 지가 알아서 다 구해준다.

import statsmodels.api as sm

lr_model = sm.Logit(y, X)
result = lr_model.fit_regularized(alpha=0.1 )
result.summary()

선형회귀분석을 하고자 할 경우 sm.OLS()를 사용하면 되고, 여기서는 로지스틱 회귀 분석이니까 sm.Logit()을 쓰면 된다. 회귀분석 적용 전에 독립변수에 원핫인코딩을 수행하는 것을 잊지 말자.

그냥 model.fit()을 적용해도 되는데, fit_regularized()를 수행하면 regularization을 수행한 최대 우도함수의 결과를 얻게 된다. 규제는 L1 규제가 디폴트로 적용되며, alpha 값의 디폴트는 0이기 때문에, alpha를 명시해주지 않으면 그냥 fit만 한거나 마찬가지니까 alpha 값을 꼭 명시해주자.

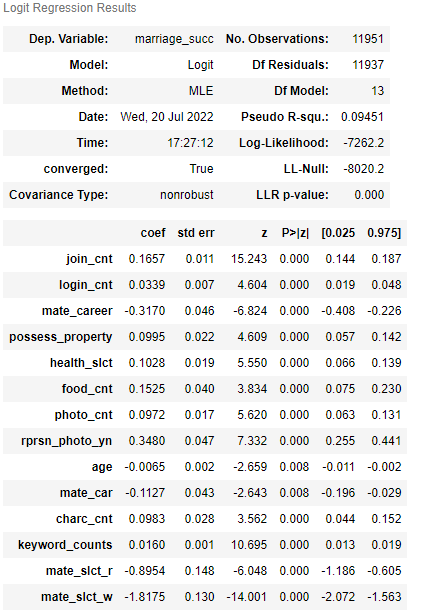
내 분석 결과는 그림과 같이 출력되었다. 총 14개의 변수가 있고, 모든 변수가 p-value 0.05 미만으로 유의함을 알 수 있다(~~사실 0.05 넘는 변수 많이 있었는데 다 지웠읍니다 ㅎ~~).

그리고 요 회귀계수를 제대로 해석하기 위해서는 각 계수에 지수 함수를 취해주어야 한다. (선형회귀랑 달리 승산비를 구하는거니까!)

np.exp(result.params)

지수함수는 numpy의 exp() 함수를 사용하면 된다. 결과를 해석해보면, join_cnt가 1 오를 때마다 1.18만큼 종속 변수가 1에 속할 확률이 증가한다고 보면 된다. mate_career가 1 오를 때마다 0.72만큼 1에 속할 확률이 감소한다고 보면 된다(1보다 작으므로 감소임).

이런 식으로 다른 변수들도 해석해 볼 수 있겠다. (참 쉽죠???? /찡긋/ )

📚 reference

정예슬

춘식이랑 함께하는 개발일지

이전 포스트