크루스칼 알고리즘

• 기본적으로 그리디한 선택을 바탕으로 알고리즘을 진행한다.
• 가장 적은 비용으로 모든 노드를 연결하기위해 사용하는 알고리즘
• 최소비용 신장트리를 만들기 위한 대표적인 알고리즘

ex) 여러개의 도시가 있을때 각 도시를 도로를 이용해 연결하려 할 때 비용을 최소한으로 하기위한 알고리즘

용어를 먼저 정리하자.

• 노드 = 정점 = 도시 : 그래프의 동그라미
• 간선 = 거리 = 비용 : 그래프의 선

핵심개념

아래와 같은 그래프가 있을 때, 크루스칼 알고리즘을 이용해 최소비용신장트리는 어떻게 만들 수 있을까?

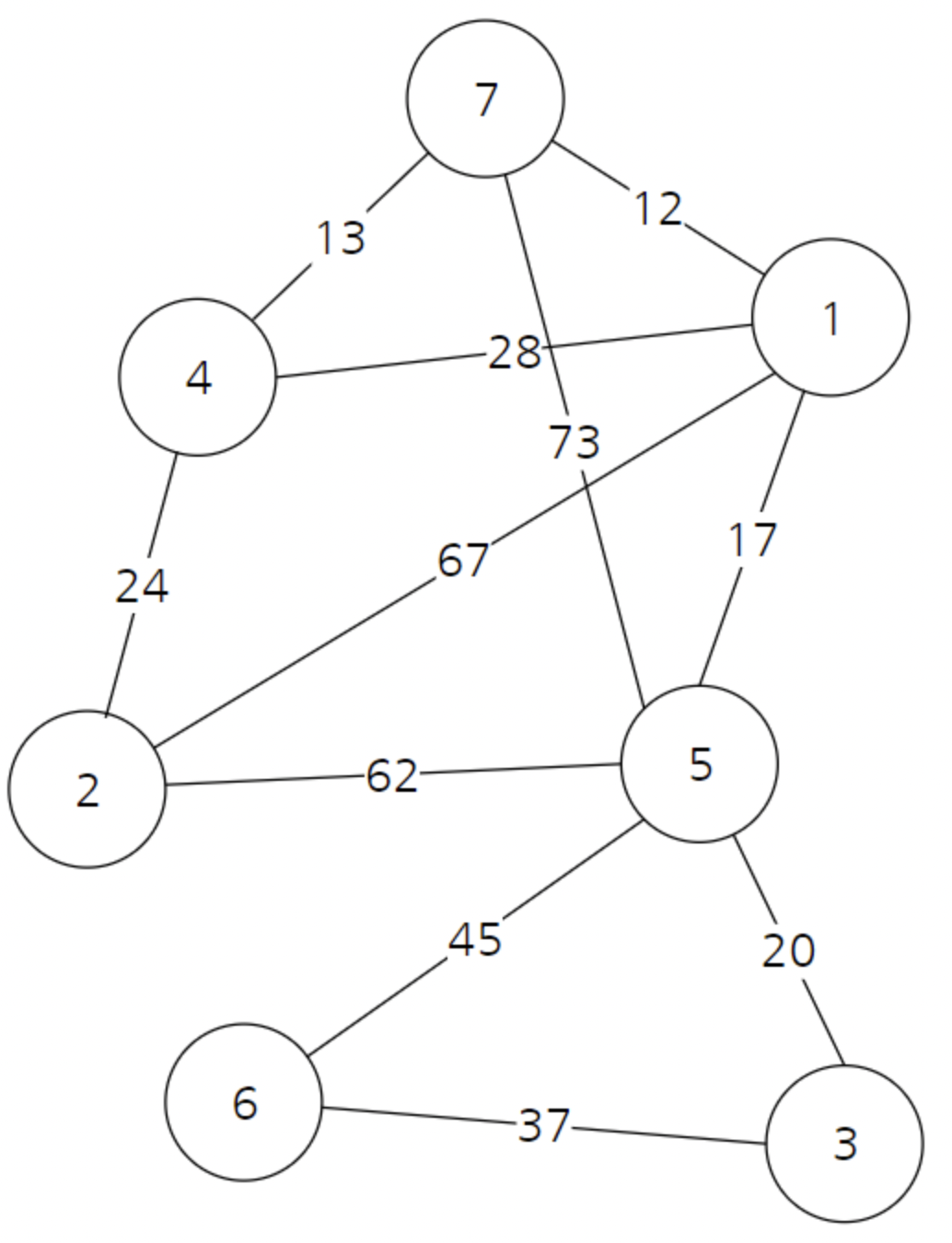
크루스칼 알고리즘의 핵심은 이것이다.

❗️간선을 거리가 짧은 순서대로 그래프에 포함시키자!

모든 노드를 최대한 적은 비용으로 연결만 시키면 되기 때문에 모든 간선정보를 오름차순으로 정렬한 뒤 비용이 적은 간선부터 차근차근 그래프에 포함시키면 된다.

이제 차례대로 그 과정을 살펴보자!

노드1부터 노드7까지 연결된 모든 간선 정보를 저장한 것이다.
노드 6,7의 간선정보가 없는 이유는 이미 다른 노드에 해당 간선정보가 포함되었기때문이다.
(즉, 양방향이라고해서 양쪽 노드 모두에 중복저장하지않는것)

모든 간선 정보에 대해 거리(비용)을 기준으로 먼저 오름차순 정렬 해준다.
이제 다음 알고리즘에 맞게 그래프를 연결하면 가장 적은 비용으로 모든 노드를 연결한 그래프인 '최소 비용 신장 트리'가 만들어 진다.

1. 정렬된 순서에 맞게 그래프에 포함시키기위한 아래 과정을 시작한다.
2. 포함시키기 전에 사이클 테이블을 확인한다.
3. 사이클을 형성하는 경우에는 그래프에 포함시키지 않는다.
4. 사이클을 형성하지 않으면 그래프에 포함시킨다.

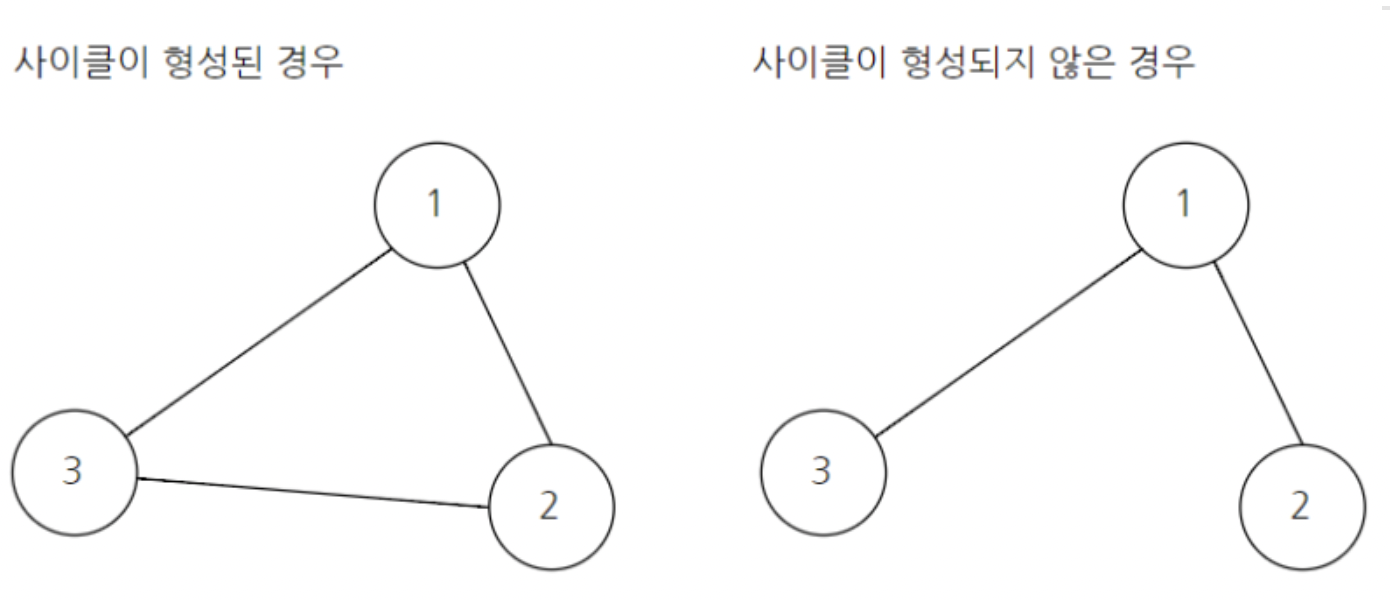
사이클
그래프가 서로 연결되어 사이클을 형성하는 것
최소비용신장트리에서는 사이클이 발생하면 안된다!
-> 애초에 모든 노드를 이어붙이기만하면 되는데, 사이클이 발생할 이유가 없는것이다.

사이클이 발생하는지 여부는 union-find알고리즘을 사용해서 알아볼 수 있다.
간선을 추가하려는 두 노드의 대표노드를 확인했는데, 동일하다면 이미 한 그래프를 이루고 있기때문에, 이 간선을 추가하면 사이클이 형성되는것이다.

예시를 통해 확인하자!

예시

아래는 초기상태이다.

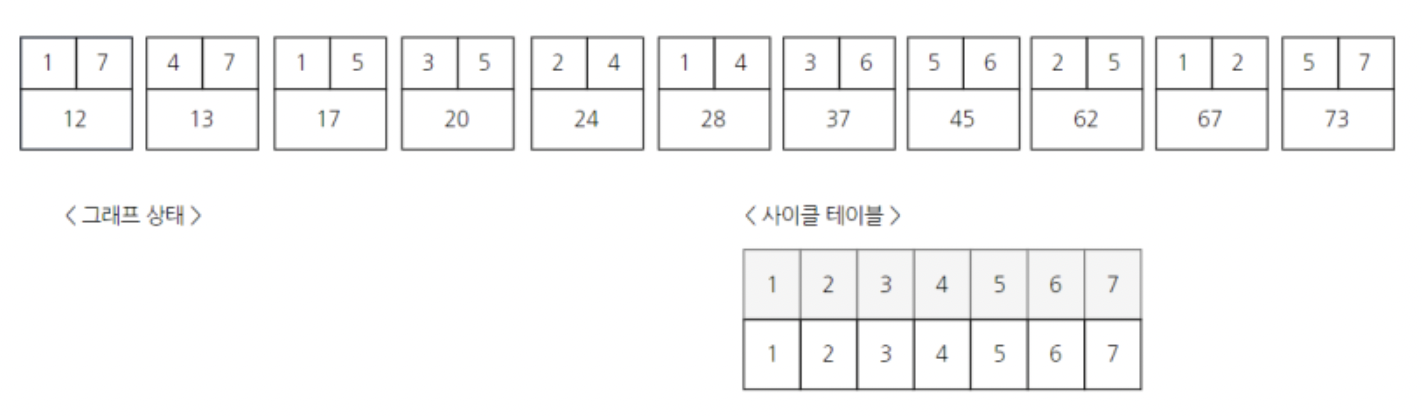
첫번째 간선부터 선택하자.

두번째 간선을 선택한다.

세번째 간선을 선택한다.

네번째 간선을 선택한다.

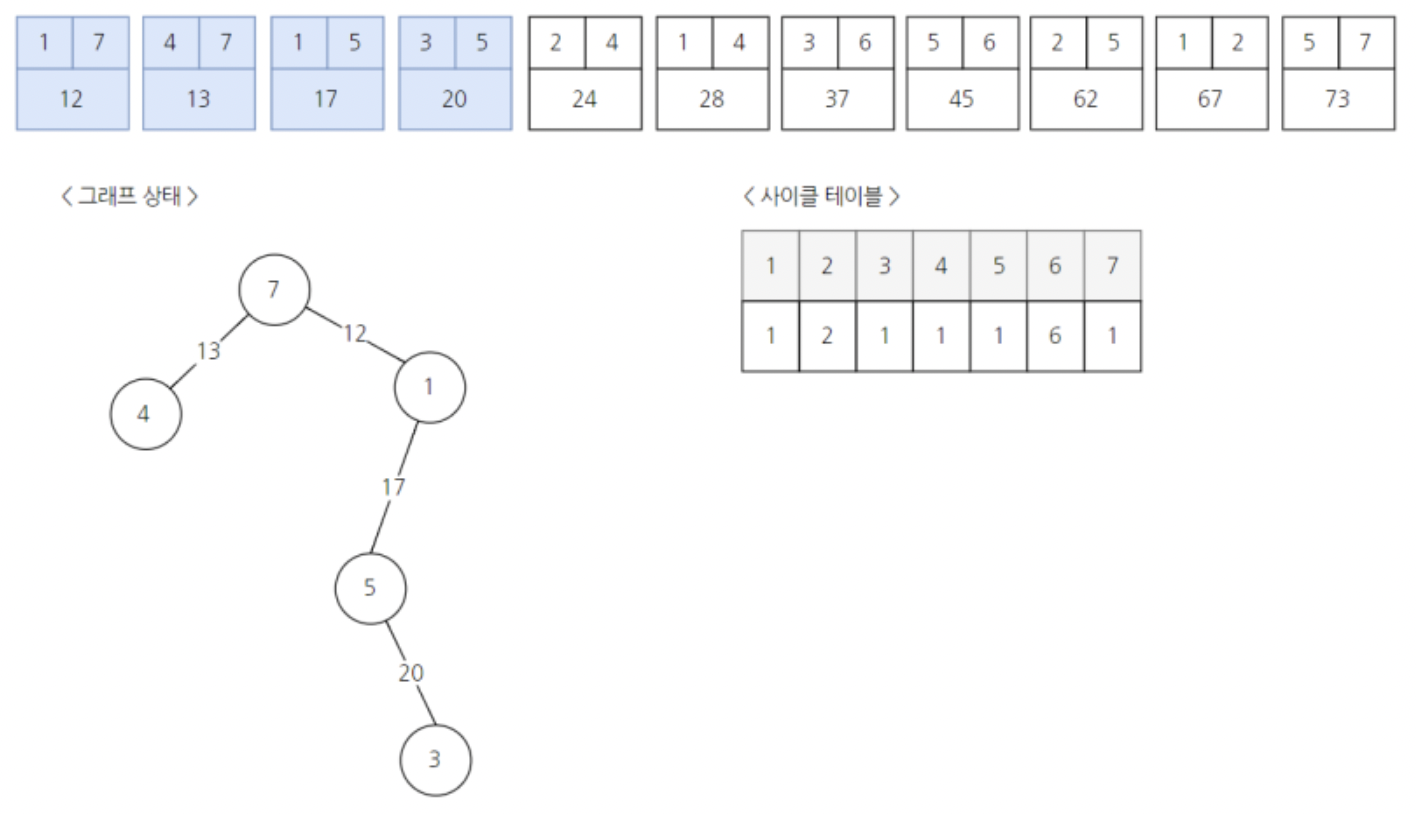
다섯번째 간선을 선택한다.

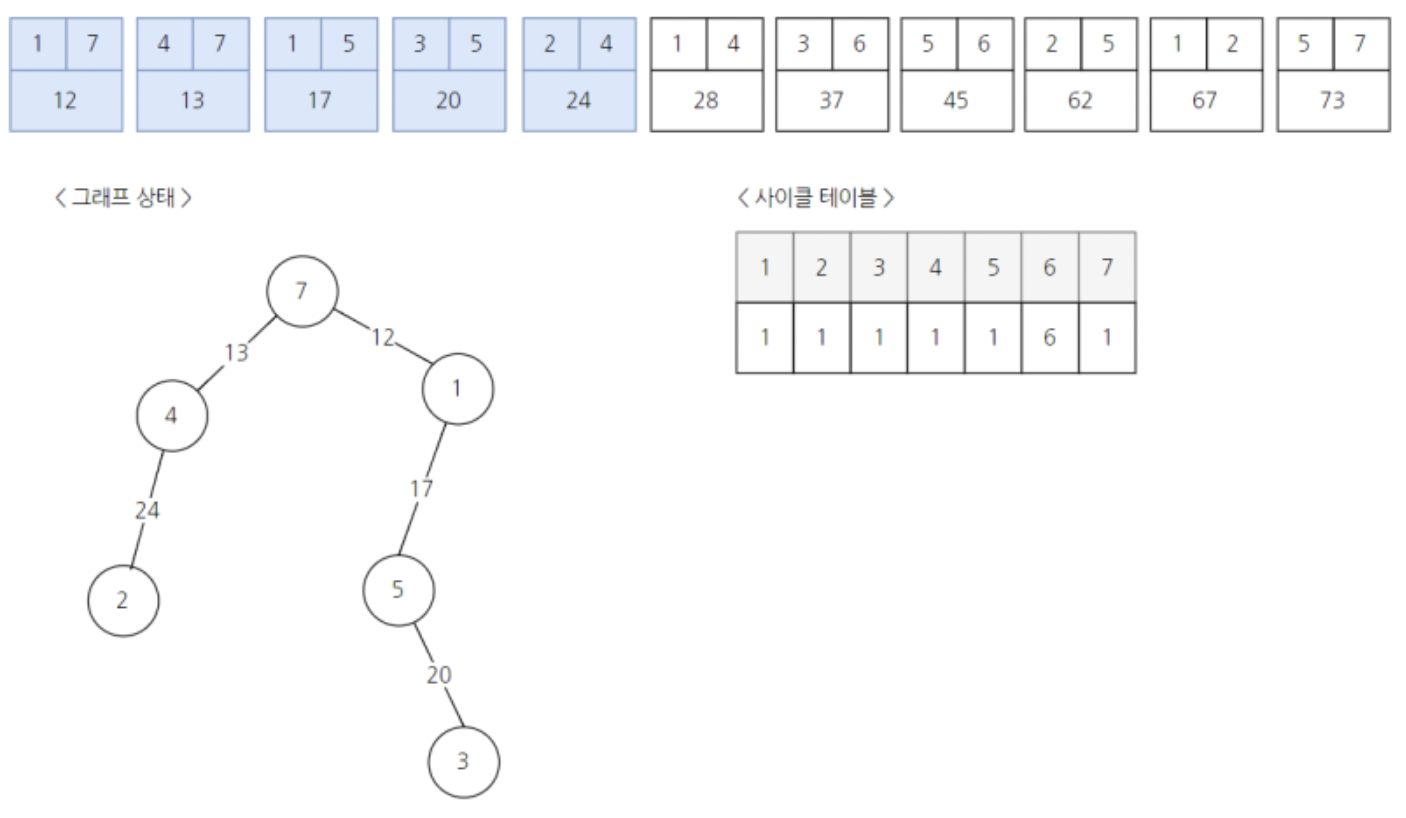
그리고 여섯번째 간선이다.
union-find알고리즘을 통해 확인하면, 이미 노드1과 노드4는 대표노드가 동일하여, 한 그래프로 연결되어있으므로 해당간선을 그래프에 포함시키지않고 넘어간다.

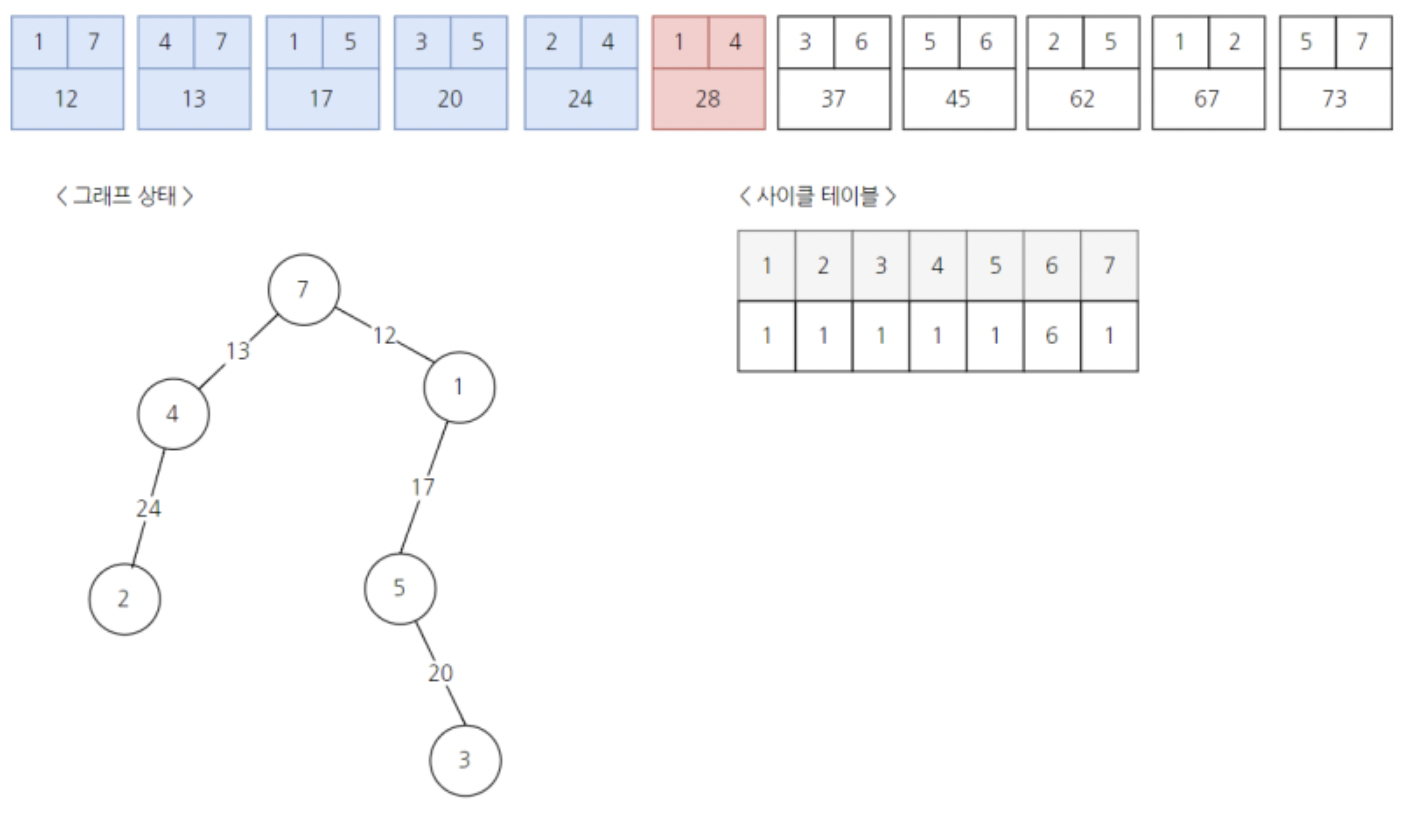
일곱번째 간선이다.

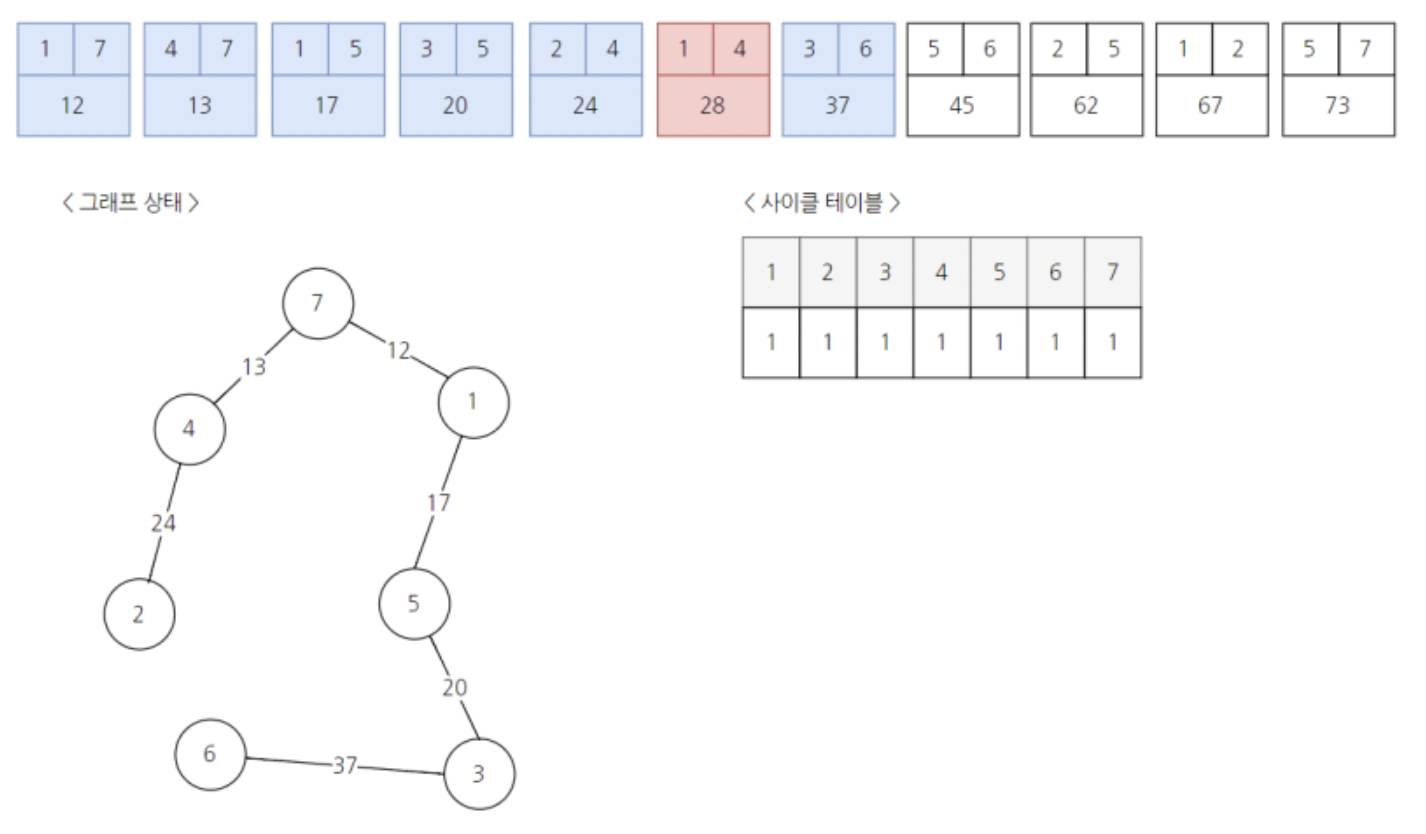
사이클 테이블의 값이 모두 대표노드 1로 맞춰지며 최소 비용 신장 트리가 형성된것을 알 수 있다.
나머지 간선은 모두 스킵처리되며, 결과적으로 다음과 같이 완성된다.

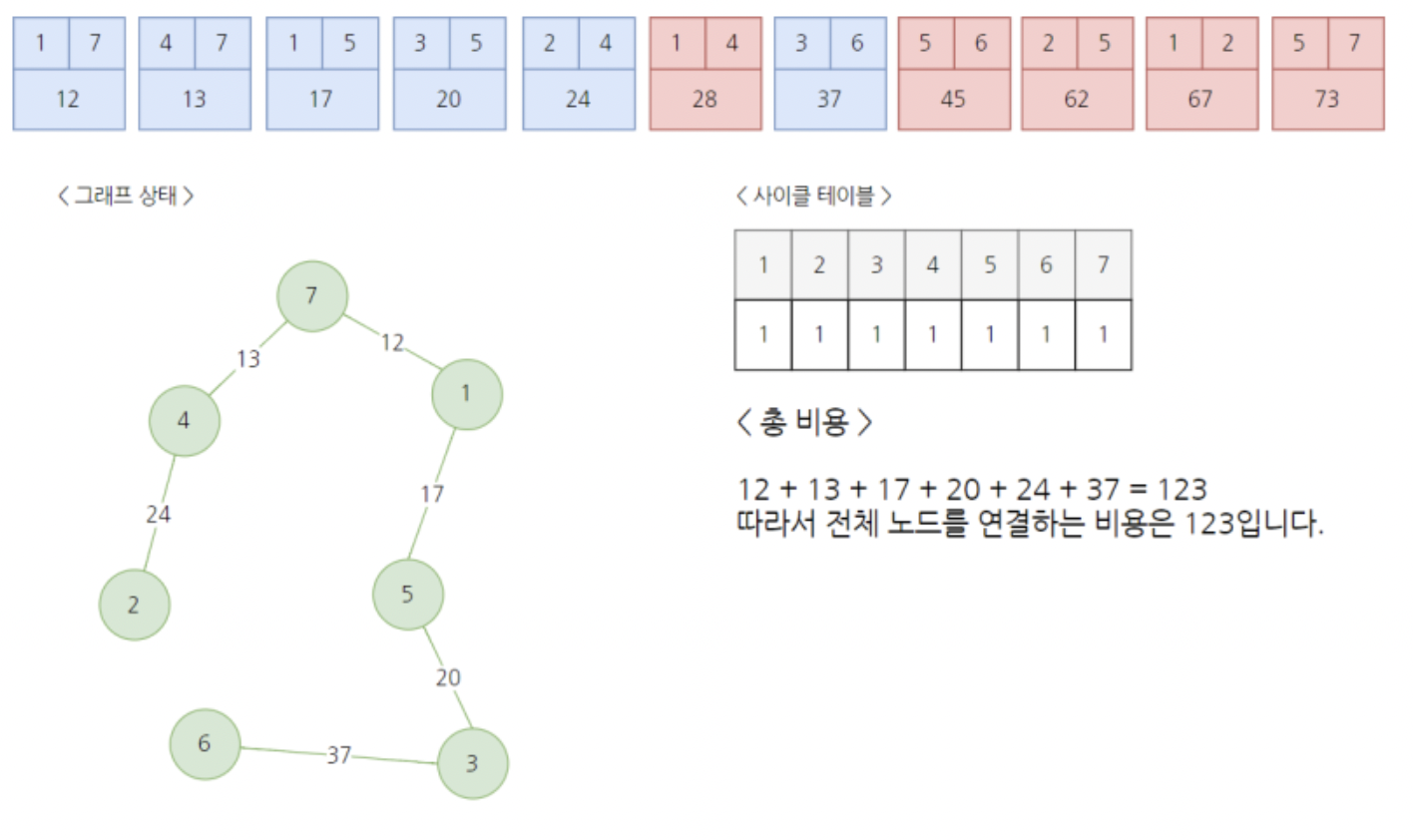
구현 - JAVA

크루스칼 알고리즘

public static void kruskal(int[][] graph, int[] parent) {
	int cost = 0;
	for(int i = 0; i < graph.length;i++) {
		if (find(parent, graph[i][0]) != find(parent, graph[i][1])) {
			cost += graph[i][2];
			union(parent, graph[i][0], graph[i][1]);
		}
	}
	System.out.println(cost);
}

전체구현

public class Main {
	// 유니온 
	public static void union(int[] parent, int x, int y) {
		x = find(parent, x);
		y = find(parent, y);
		
		if(x < y) parent[y] = x;
		else parent[x] = y;
	}
    // 파인드
	public static int find(int[] parent, int x) {
		if(parent[x] == x) return x;
		else return find(parent, parent[x]);
	}
	
    // 크루스칼
	public static void kruskal(int[][] graph, int[] parent) {
		int cost = 0;
		for(int i = 0; i < graph.length;i++) {
			if (find(parent, graph[i][0]) != find(parent, graph[i][1])) {
				cost += graph[i][2];
				union(parent, graph[i][0], graph[i][1]);
			}
		}
        
        // 최소 신장 트리의 총 가중치 출력
		System.out.println(cost);
	}
	
	public static void main(String[] args) throws IOException {
    	// 간선 입력 받기, 그래프에 저장
		BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(bf.readLine());
		int m = Integer.parseInt(bf.readLine());
		int[][] graph = new int[m][3];
		
		StringTokenizer st;
		for (int i = 0; i < m; i++) {
			st = new StringTokenizer(bf.readLine());
			graph[i][0] = Integer.parseInt(st.nextToken()); // 간선 나가는 정점
			graph[i][1] = Integer.parseInt(st.nextToken()); // 간선 들어오는 정점
			graph[i][2] = Integer.parseInt(st.nextToken()); // 가중치
		}
		
        // 간선 정렬
		Arrays.sort(graph, (o1, o2) -> o1[2] - o2[2]);
		
        // 부모노드 초기화
		int[] parent = new int[n + 1];
		for (int i = 0; i < parent.length; i++) {
			parent[i] = i;
		}
        
		//크루스칼 알고리즘 수행
		kruskal(graph, parent)
	}
}

입력
5
6
1 3 3
1 4 8
4 5 9
1 2 10
2 3 13
2 5 14

출력 결과
30

시간복잡도

크루스칼 알고리즘 = 정렬 알고리즘 + union find알고리즘
따라서 크루스칼의 시간복잡도는 정렬 알고리즘의 시간복잡도와 동일하다고 판단해도 큰 무리가 없다. 따라서 O(ElogE)

참조
https://m.blog.naver.com/ndb796/221230994142
https://velog.io/@suk13574/알고리즘Java-크루스칼Kruskal-알고리즘