D3VO: Deep Depth, Deep Pose and Deep Uncertainty for Monocular Visual Odometry (CVPR 2020)
Paper read
Abstract
Deep monocular visual odometry - Deep depth, pose and uncertainty estimation 3가지 를 이용해서 SLAM에 접목해보겠다.
- self-supervised learning trained on stereo videos
=> predictive brightness transformation parameter
- Photometric uncertainties of pixels on the input image => depth estimation accuracy, provides a learned weighting functions for the photometric residuals in direct VO.
Introduction
인접한 image들에 대해 depth를 이용하여 pose를 구할 수 있던 과거 전례에 기반
self-supervised learning
=> DepthNet, PoseNet 간의 photometric error (static warping, temporal warping), temporal information => accurate depth
=> light inconsistent를 보완하기 위한 transformation parameter => accurate depth를 초래
1) predicted depth를 기반한 3D point로 initialize.
2) virtual stereo term: 예측된 pose에 대한 non-linear optimization을 진행하기 위함
=> our network는 any external depth supervision 없이 오직 stereo videos만을 이용
- Photometric uncertainties: brightness constancy assumption을 벗어나는 error들이 줄어듦.
photometric residuals의 learned weight 는 direct VO와 함께 사용될 수 있다. direct VO도 photometric objective를 썼기때문에. 기존 traditional direct VO를 본 논문의 weight function을 바꿔보자는 의도
Method
Self-supervised Network
target 이미지 와 source 이미지 }에 대한 loss ( 와 의 변환관계는 stereo 알고있음)
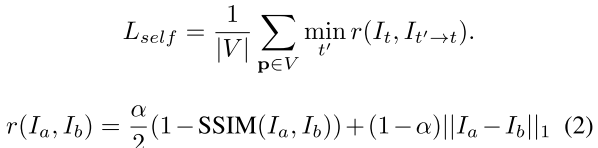
The common practice of photometric error
그러나 대부분의 data들은 illumination changes가 많아서 학습 및 성능에 악영향을 끼친다.
-> Brightness transformation parameter를 이용하여 camera exposure change를 modeling해보자.
Brightness transformation parameter
- image intensity의 변화를 affine transform으로 정의해보자. 기존 연구들에서 좋은 성과를 보여줌.
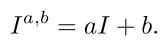
위 식을 반영한 최종 Loss 식을 아래와 같이 정의하자
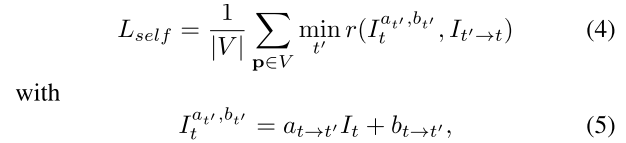
Photometric error
brightness change 이외에 더 보완해줄 방법 (non-Lambertian surface와 같은 잘 안되는 case 존재)
이런 부분들을 불확실성의 개념으로 접근 => uncertainty를 줄이는 방향으로 학습
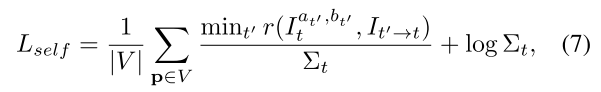
따라서 최종적인 Loss function은 아래와 같음
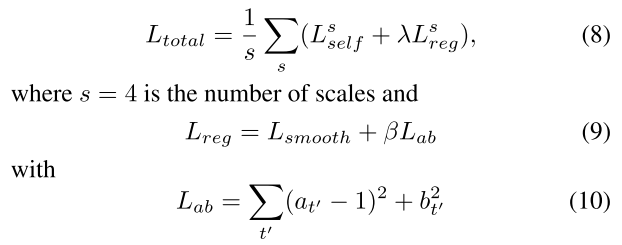
smooth는 edge-aware smoothness on Dt
D3VO
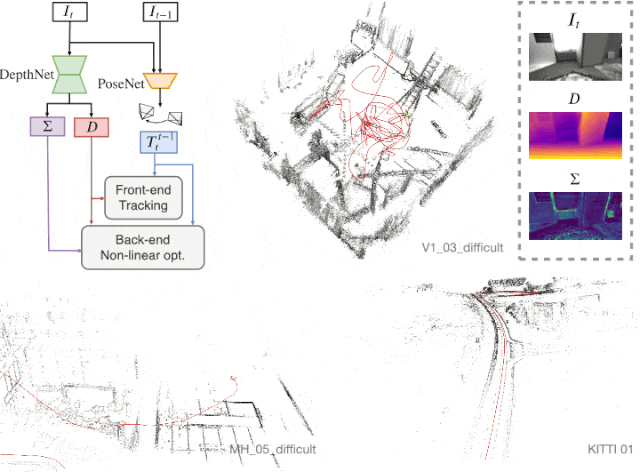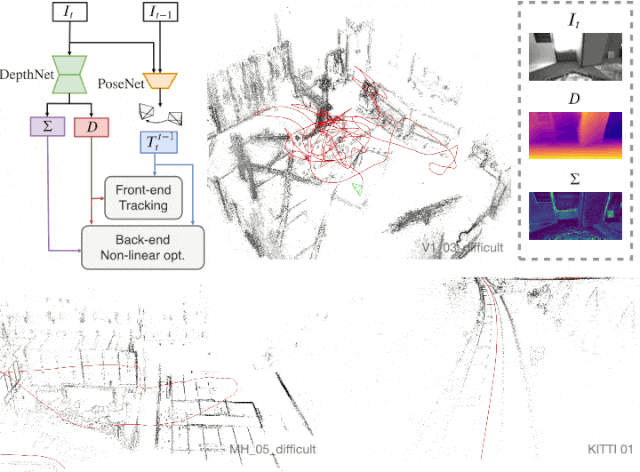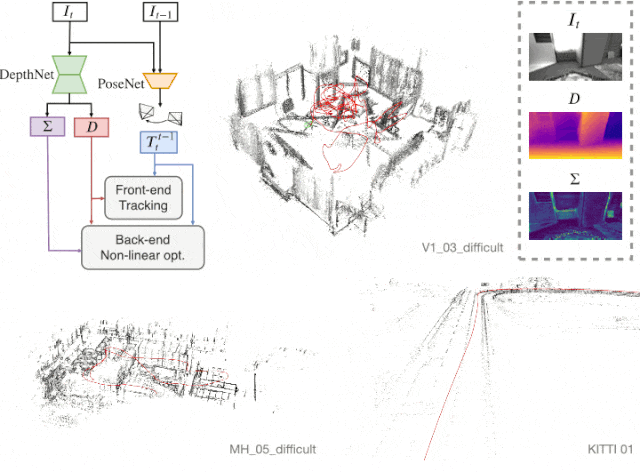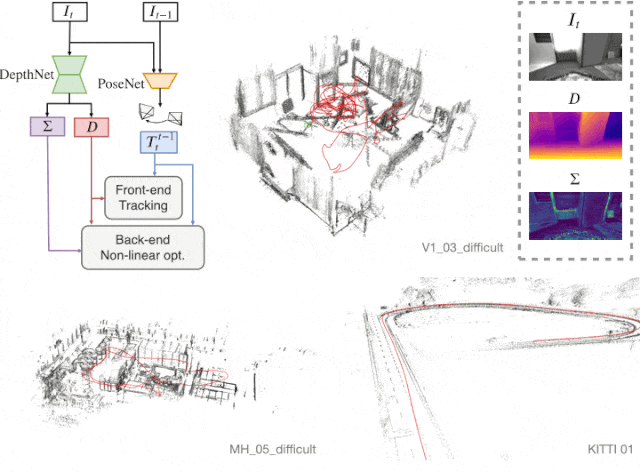
본 단락은 Self-supervised learning으로 획득한 정보 (Depth, Pose, Uncertainty)를 이용하여, SLAM의 backend 알고리즘에 활용하고자 하는 단락이다. 먼저 total 에너지 함수는 다음과 같다.

크게 photo에 대한 부분과 pose에 대한 부분으로 이루어져 있다.
먼저 pose term을 살펴보면 다음과 같다.
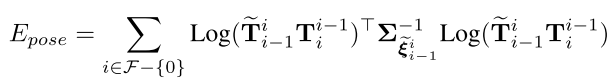
모든 frame-to-frame pose에 대한 정보가 tilda_T이고 key frame pose에 대한 정보는 T이다.
Error function을 최적화 하기 위한 방법으로써 많이 활용되는 Gauss-Newton 방법을 활용하였고, diagonal inverse covariance matrix인 sigma_inv는 각 componant에 대해 에러에 대한 weight를 부여하기 위한 행렬이다.
이후 photo term을 살펴보면 다음과 같다.

먼저 (17)을 살펴보면, depth에 관한 정보 d_p는 backend 이전에서 predict했던 tild_D를 이용하여 3D point로 projection(PI 함수)한 후, extrinsic에 대한 information을 곱해준 후, 다시 2D point로 mapping 시키는 일련의 과정이다. 결국, 15, 16, 17번 식은 reprojection error function을 optimization하기 위한 error function임을 확인할 수 있다.
다음으로 14번의 오른쪽 term에 있는 수식을 살펴보면 아래와 같다.
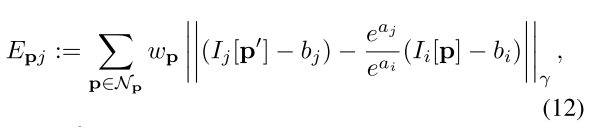
a, b는 앞쪽에서 구했던, brightness를 맞춰주기 위한 affine transform parameter들이다.
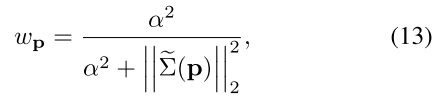
backend 이전에서 구한 uncertainty를 활용하였고, uncertainty에 대한 weight를 부여하기 위해 위와 같이 식을 설계하였다.
수식 12, 13번과 같은 경우 논문에서도 알 수 있 듯이, Direct sparse odometry의 수식을 그대로 차용한 것을 확인할 수 있다. 위 수식을 이해하기 위해서는 이 논문은 먼저 살펴보는 것이 좋을 듯 하다.
