Projective Geometry - 2D: Homography

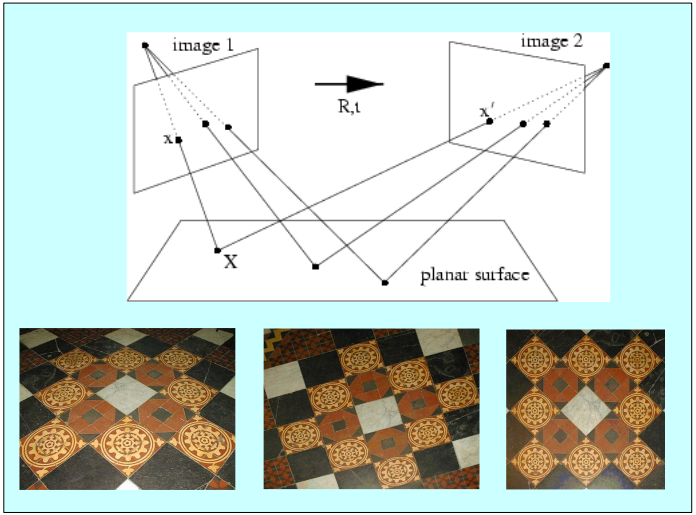
Homography (Projective Transformation)

• Definition : A mapping $h(.): P^2 => P^2$ such that

  $x_1, x_2, x_3 \ \ \ lie \ on \ the \ same \ line => h(x_1), h(x_2), h(x_3)$

• Transformation

Equation of 2D projective Transformations ( where $H$ could be 3 x 3 matrix )

Point: $x' = Hx$

Line : $l' = H^{-T}l \ \ where \ \ H^{-T} = (H^{-1})^T$

$\because$ $\ \ \ l^Tx=0$, $l^Tx = l^T(H^{-1}x') = (l^TH^{-1})x'$

$\therefore$ $(l^TH^{-1})x' = 0$

Hierarchy of Projective Transformations

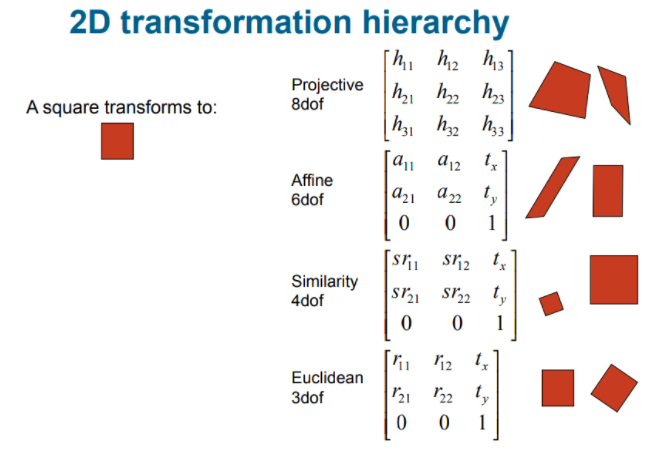
• Isometries(Euclidean)
• Similarity Transformations
• Affine Transformations
• General Projective Transformations

Properties of Projective Transformations

• Vanishing lines
• Decompositions