Rectification (Affine, Metric) with Vanishing Point

Affine rectification

i) Taking two parallel lines and find the vanishing line.
ii) Taking a vanishing line that is in a finite space into a line at infinity $(0,0,1)$

iii) Doing Homography : Two line that do have not Parrellel relationship are retificated.

Metric retification

i Pairs of line that were originally vertical in the image. Finding constraint $s$ in this equation:

Based on the example, we do SVD to solve the linear equations of $AS = 0$, and the last column of vector is used as the solution.

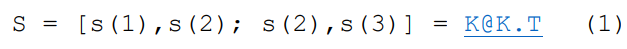
Using Equation, we can obtain CDCP, linear with AS = 0

If you put sqrt on the diagonal component in $U, D, V^T = svd(S)$ on the result of svd $S$
$H = [K,0;0,1]$ corresponding to the affine matrix can be obtained. Affine as $Inv(H)$
If you do homography on the rectified image, the metric rectified image is comes out.

Five pairs of straight lines can be given for CDCP with dof of 5 in the following way,
This is the process of finding the solution of the linear equation, and CDCP can be obtained. After that the above process repeat.

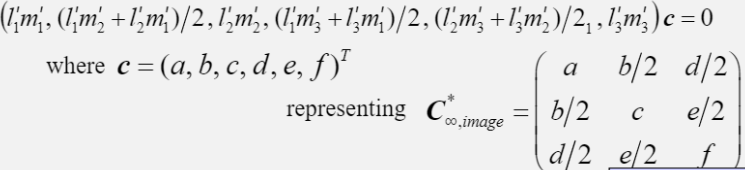
$C^*_{image}$ can be obtained by using five pairs of orthogonal lines.