Kruskal

CHOYEAH·2023년 11월 1일
알고리즘
0
post-custom-banner

개념

Kruskal의 알고리즘은 연결된 무방향 그래프에 대한 최소 스패닝(신장) 트리를 찾는 그래프 이론의 그리디 알고리즘입니다. 최소 스패닝(신장) 트리는 그래프의 모든 노드를 사이클이 발생하지 않게끔 간선의 총 가중치가 가장 작은 것으로 연결합니다. 알고리즘은 가장 낮은 가중치에서 가장 높은 가중치까지 모든 에지를 정렬하고 이미 연결된 에지로 사이클을 형성하지 않는 경우에만 스패닝 트리에 추가하는 방식으로 작동합니다.

신장트리에서 사이클이 없는 최소 가중치로 구성된 최소 신장트리를 구하는 알고리즘
이를 구하는 전략으로 가중치값을 기준으로 내림차순 정렬을 하여 사용한다.
트리에 사이클이 없도록 구성하기 위해서 유니온 파인드 알고리즘을 사용한다.

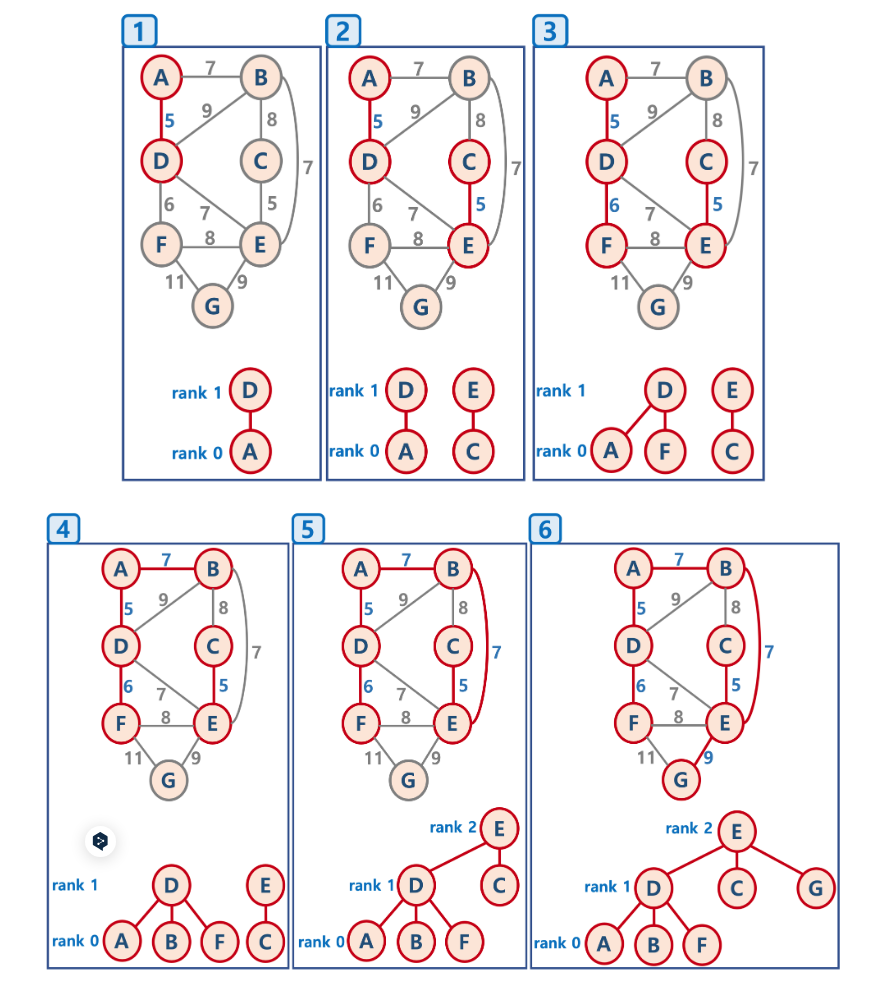
크루스칼 알고리즘의 로직 프로세스

  1. 모든 정점을 독립적인 집합으로 만든다.
  2. 모든 간선을 비용을 기준으로 내림차순 정렬한다.
  3. 정렬된 간선으로 루프를 돈다.
  4. 간선으로 이어진 두 노드의 부모를 가져와 비교한다
  5. 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. 그리고 최소신장트리 결과값 변수에 저장한다. (최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임)
  6. 최소신장트리 결과값 변수를 리턴한다.

탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)

장점

  1. 최적 결과: 알고리즘은 항상 그래프의 최소 스패닝 트리(있는 경우)를 찾습니다.
  2. 단순성: Kruskal의 알고리즘은 다른 최소 스패닝 트리 알고리즘보다 개념적으로 이해하기 쉽고 구현하기 쉽습니다.
  3. 시작 노드 필요없음: Prim의 알고리즘과 달리 Kruskal의 알고리즘은 특정 시작 노드가 필요하지 않습니다.

단점

  1. 연결된 그래프 필요: 그래프가 연결되지 않으면 Kruskal의 알고리즘이 제대로 작동하지 않습니다.
  2. 사이클 감지: 에지를 추가하면 사이클이 형성되는지 여부를 감지하는 것은 알고리즘을 구현하는 데 사용되는 데이터 구조에 따라 시간 복잡도 측면에서 비용이 많이 들 수 있습니다.

사용에 적절한 상황

Kruskal의 알고리즘은 연결된 무방향 그래프가 있고 최소 스패닝 트리를 결정해야 할 때 가장 유용합니다. 이는 특히 통신 네트워크, 컴퓨터 네트워크, 운송 네트워크 및 유틸리티 그리드 설계와 같은 네트워크 설계와 관련된 문제에 적용할 수 있습니다.

사용에 부적절한 상황

Kruskal 알고리즘은 그래프가 연결되어 있지 않으면 스패닝 트리를 형성할 수 없으므로 사용하면 안 됩니다. 또한 유방향 그래프에는 적용되지 않습니다.

지침

그래프에 사이클이 형성되는 상황이 발생하기 쉬우므로 알고리즘 구현 시 주의가 필요합니다.

시간 복잡도

크루스컬 알고리즘의 시간 복잡도는 O(E log E)이다.
크루스칼 알고리즘에는 크게 세 가지의 파트로 나눌 수 있는데

  1. 모든 정점을 독립적인 집합으로 만듦: O(V)

  2. 모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.: O(E log E)

    퀵소트를 사용한다면 시간 복잡도는 O(n log n) 이며, 간선이 n이므로 O(E log E)

  3. 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. O(1)

    union-by-rank 와 path compression 기법 사용시 시간 복잡도가 결국 상수값에 가까움, O(1)

    • 상세설명: 두 가지 최적화 기법인 "union-by-rank"와 "path compression"을 사용하면 Union-Find 연산의 시간복잡도를 거의 상수 시간에 가깝게 만들 수 있습니다.

      1. Union-by-Rank: 이 기법에서는 각 노드에 "랭크(rank)"를 유지하며, 랭크는 해당 노드가 속한 트리의 높이를 나타냅니다. 두 집합을 합칠 때는 작은 랭크의 루트가 큰 랭크의 루트 아래에 오도록 합니다. 이를 통해 트리의 높이가 불필요하게 증가하는 것을 방지하며, 이는 연산의 시간복잡도를 개선하는데 기여합니다.

      2. Path Compression: 이 기법은 Find 연산을 수행할 때 경로 상의 각 노드가 직접 루트를 가리키도록 하는 것입니다. 이는 모든 찾기 연산이 빠르게 수행될 수 있게 하며, 더욱 중요한 것은 연속적인 찾기 연산이 각 트리를 점점 더 플랫하게 만든다는 점입니다.

        이 두 가지 기법을 사용할 경우, Union-Find 알고리즘의 시간 복잡도는 거의 O(1), 즉 상수 시간에 가까워집니다. 그러나 이는 "아모티즈드(amortized)" 시간 복잡도라는 점을 명심해야 합니다. 즉, 개별적인 연산은 O(1)보다 느릴 수 있지만, 여러 연산을 걸쳐 평균화하면 그 비용은 상수 시간에 가깝게 됩니다.

        이러한 성능 향상이 가능한 이유는, 트리의 높이를 최소화하고 경로를 압축함으로써 연산 경로를 최적화하기 때문입니다. 랭크에 의한 유니온과 경로 압축은 함께 사용될 때 가장 효과적입니다. 둘 다 사용하면 각 연산의 시간 복잡도는 반복적으로 호출될 때 상당히 효율적인 O(α(n))이 됩니다. 여기서 α(n)은 아커만 함수의 역함수로서, n이 실제 컴퓨터에서 다루는 모든 가능한 값의 범위에 대해 매우 작은 값을 가집니다. 그 결과, 시간 복잡도가 거의 O(1)에 가깝게 된다고 볼 수 있습니다.

    최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임

따라서 2번, 간선을 기준으로 정렬하는 시간에 크루스컬 알고리즘의 시간복잡도가 좌우된다. 즉 간선을 기준으로 정렬하는 시간이 가장 크다.

코드구현

JavaScript

class UnionFind {
  // UnionFind 클래스는 생성될 때 그래프를 인자로 받습니다
  constructor(graph) {
    this.parent = {};
    this.rank = {};

    // 그래프의 모든 정점을 각각 독립된 집합으로 초기화합니다
    for (let vertex of graph.vertices) {
      this.parent[vertex] = vertex; // 모든 원소들이 자기 자신을 부모로 가집니다
      this.rank[vertex] = 0; // 모든 노드의 랭크를 0으로 초기화합니다;
    }
  }

  // Path Compression 기법을 이용한 Find 함수
  find(node) {
    if (this.parent[node] !== node) {
      this.parent[node] = this.find(this.parent[node]); // 루트 노드를 찾을때까지 재귀 호출
    }
    return this.parent[node]; // 인자로 전달된 노드의 루트 노드 리턴
  }

  // Union-by-Rank 기법을 이용한 Union 함수
  union(u, v) {
    let uRoot = this.find(u); // u의 루트를 찾습니다
    let vRoot = this.find(v); // v의 루트를 찾습니다

    // 같은 집합에 속해 있다면, 합칠 필요가 없습니다
    if (uRoot === vRoot) return;

    // 랭크에 의한 유니온:
    if (this.rank[uRoot] > this.rank[vRoot]) {
      this.parent[vRoot] = uRoot; // u의 랭크가 v의 랭크보다 높다면, v의 루트를 u로 합니다
    } else if (this.rank[uRoot] < this.rank[vRoot]) {
      this.parent[uRoot] = vRoot; // v의 랭크가 u의 랭크보다 높다면, u의 루트를 v로 합니다
    } else {
      this.parent[vRoot] = uRoot; // 랭크가 같다면, 하나를 루트로 지정하고 그 랭크를 1 증가시킵니다
      this.rank[uRoot]++;
    }
  }
}

function kruskal(graph) {
  // 그래프의 간선들을 가중치 기준으로 정렬합니다
  const edges = graph.edges.sort((a, b) => a.weight - b.weight);

  // UnionFind의 인스턴스를 생성하고, 그래프를 이용하여 초기화합니다
  const uf = new UnionFind(graph);
  const mst = []; // 최소 신장 트리를 저장하는 배열입니다

  for (let edge of edges) {
    // 두 노드가 같은 집합에 속하지 않는다면
    if (uf.find(edge.src) !== uf.find(edge.dest)) {
      // 두 노드를 합치고, 해당 간선을 MST에 추가합니다
      uf.union(edge.src, edge.dest);
      mst.push(edge);
    }
  }

  // 최소 신장 트리를 반환합니다
  return mst;
}

const graph = {
  vertices: ["A", "B", "C", "D", "E", "F", "G"],
  edges: [
    { src: "A", dest: "B", weight: 7 },
    { src: "A", dest: "D", weight: 5 },
    { src: "B", dest: "A", weight: 7 },
    { src: "B", dest: "C", weight: 8 },
    { src: "B", dest: "D", weight: 9 },
    { src: "B", dest: "E", weight: 7 },
    { src: "C", dest: "B", weight: 8 },
    { src: "C", dest: "E", weight: 5 },
    { src: "D", dest: "A", weight: 5 },
    { src: "D", dest: "B", weight: 9 },
    { src: "D", dest: "E", weight: 7 },
    { src: "D", dest: "F", weight: 6 },
    { src: "E", dest: "B", weight: 7 },
    { src: "E", dest: "C", weight: 5 },
    { src: "E", dest: "D", weight: 7 },
    { src: "E", dest: "F", weight: 8 },
    { src: "E", dest: "G", weight: 9 },
    { src: "F", dest: "D", weight: 6 },
    { src: "F", dest: "E", weight: 8 },
    { src: "F", dest: "G", weight: 11 },
    { src: "G", dest: "E", weight: 9 },
    { src: "G", dest: "F", weight: 11 },
  ],
};

console.log(kruskal(graph)); // 최소 신장 트리의 간선 목록을 출력합니다
// result
// [
//   { src: "A", dest: "D", weight: 5 },
//   { src: "C", dest: "E", weight: 5 },
//   { src: "D", dest: "F", weight: 6 },
//   { src: "A", dest: "B", weight: 7 },
//   { src: "B", dest: "E", weight: 7 },
//   { src: "E", dest: "G", weight: 9 },
// ]

Python

   parent = dict()
   rank = dict()
   
   def find(node):
       # path compression 기법
       if parent[node] != node:
           parent[node] = find(parent[node])
       return parent[node]
   
   def union(node_v, node_u):
       root1 = find(node_v)
       root2 = find(node_u)
       
       # union-by-rank 기법
       if rank[root1] > rank[root2]:
           parent[root2] = root1
       else:
           parent[root1] = root2
           if rank[root1] == rank[root2]:
               rank[root2] += 1
       
       
   def make_set(node):
       parent[node] = node
       rank[node] = 0
   
   def kruskal(graph):
       mst = list()
       
       # 1. 초기화
       for node in graph['vertices']:
           make_set(node)
       
       # 2. 간선 weight 기반 sorting
       edges = graph['edges']
       edges.sort()
       
       # 3. 간선 연결 (사이클 없는)
       for edge in edges:
           weight, node_v, node_u = edge
           if find(node_v) != find(node_u):
               union(node_v, node_u)
               mst.append(edge)
       
       return mst
   
   mygraph = {
       'vertices': ['A', 'B', 'C', 'D', 'E', 'F', 'G'],
       'edges': [
           (7, 'A', 'B'),
           (5, 'A', 'D'),
           (7, 'B', 'A'),
           (8, 'B', 'C'),
           (9, 'B', 'D'),
           (7, 'B', 'E'),
           (8, 'C', 'B'),
           (5, 'C', 'E'),
           (5, 'D', 'A'),
           (9, 'D', 'B'),
           (7, 'D', 'E'),
           (6, 'D', 'F'),
           (7, 'E', 'B'),
           (5, 'E', 'C'),
           (7, 'E', 'D'),
           (8, 'E', 'F'),
           (9, 'E', 'G'),
           (6, 'F', 'D'),
           (8, 'F', 'E'),
           (11, 'F', 'G'),
           (9, 'G', 'E'),
           (11, 'G', 'F')
       ]
   }
   
   kruskal(mygraph)
   
   // 결과
   [(5, 'A', 'D'),
    (5, 'C', 'E'),
    (6, 'D', 'F'),
    (7, 'A', 'B'),
    (7, 'B', 'E'),
    (9, 'E', 'G')]
profile
CHOYEAH
Move fast & break things
이전 포스트

Union Find

다음 포스트

Prim

post-custom-banner

0개의 댓글