lec 02
Contents
- What is Linear regression?
- What is Hypothesis?
- Hypothesis
- H(x) = Wx + b
- Which hypothesis is better?
- Cost / Loss function
- Const function
- Loss function
ㅤ
ㅤ
ㅤ
ㅤ
1. linear regression(선형 회귀)
아래는 공부 시간에 따른 시험 점수를 기록한 training data이다.
| x (hour) | y (score) |
|---|---|
| 10 | 9 |
| 9 | 80 |
| 5 | 50 |
| 3 | 20 |
이 데이터를 regression 모델에게 학습 시키면 x에 따른 y값을 알아낼 수 있다.
만약 x의 값을 7로 준다면, regression 모델은 y의 값이 60~70 사이 이라고 예측할 수 있다.
이를 Linear regression (선형 회귀)라고한다.
Linear regression(선형 회귀)은 regression(회귀)의 한 종류,
입력과 출력 사이의 선형 관계를 가정하여 모델링하는 방법
입력 변수와 출력 변수 사이의관계를 하나의 직선으로 모델링하려는 시도로 이해할 수 있음.
ㅤ
ㅤ
ㅤ
주의주의
하지만 실제 데이터는 모두가 선형적인 경향을 보이지는 않으며, 비선형적인 특성을 가진 경우도 많이 있다.
따라서 데이터가 선형적인지 아닌지를 사전에 확인하고, 만약 비선형적인 경향이 있다면 다른 비선형 회귀 기법을 사용해야 한다.
ㅤ
리니어 리그레이션(Linear Regression)은 입력과 출력 사이의 선형적인 관계를 모델링하는 회귀 기법이다.
이를 위해 주어진 데이터에 가장 잘 맞는 선(규칙)을 찾는 것이 목표.
ㅤ
ㅤ
ㅤ
ㅤ
2. Hypothesis (가설)
가설을 세우는 방법은 아래와 같다.
H(x) = Wx + b
W = 가중치(weight), b = 편향(bias)
ㅤ
hypothesis(가설)
Linear regression(선형 회귀)에서의 가설은
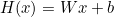
와 같이 주어진 데이터에 대해 입력 x와 출력 y 사이의 선형적인 관계를 모델링하는 함수이다.
ㅤ
아래의 가설을 보면 이해하기 쉬울 것이다.
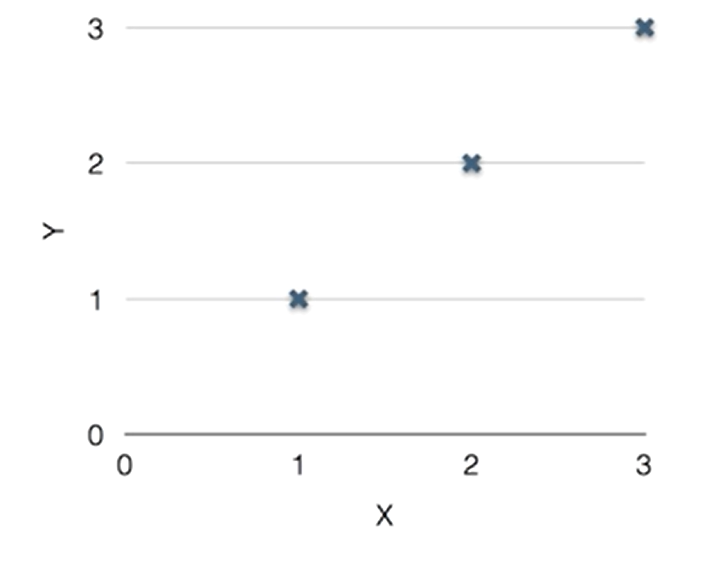
리니어 리그레이션의 핵심은 주어진 데이터에 가장 잘 맞는 가중치 W와 편향 b를 찾는 것,
이를 위해 학습 데이터를 사용하여 모델을 학습하고, 손실 함수를 최소화하는 방향으로 W와 b를 조정한다.
ㅤ
ㅤ
ㅤ
ㅤ
Which hypothesis is better?
그렇다면 어떤 가설이 가장 좋을까?
실제 데이터와 가설 사이의 오차를 살펴보는 것이 중요하다.
오차가 작을수록 모델이 실제 데이터를 잘 반영한 것으로 간주할 수 있고, 이를 통해 최적의 모델과 하이퍼를 선택하여 더 정확한 예측을 수행할 수 있기 때문이다.
ㅤ
ㅤ
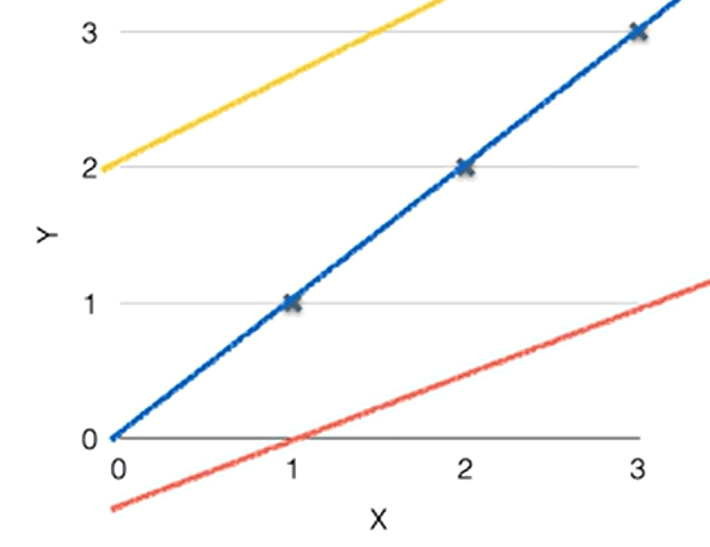
아래 각각의 빨강, 파랑, 노랑색의 선들을 가설이라고 하고 점을 실제 데이터라고 하다면,
점과 오차 범위가 가장 적은 파랑 선이 가장 좋은 가설이라고 할 수 있다.
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
3 . Cost / Loss function
그렇다면 빨간색 선과 점 사이의 거리는 어떻게 구할까?
regression에서 cost function을 사용하면 디스턴스(두 점 또는 객체 사이의 거리)를 간단하게 구할 수 있다.
가설과 실제 데이터 빼기
1.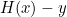
하지만 이렇게하면 실제 데이터가 음수일 때, -y가 양수가 되어버리니 추천하지않는다.
ㅤ
ㅤ
가설과 실제 데이터 빼고 제곱하기
2.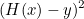
y가 음수라도 제곱으로 양수로 만들어 줄 수 있으니 최고다.
ㅤ
ㅤ
실제 데이터와 가설의 디스턴스를 구하는 식은 아래와 같다.
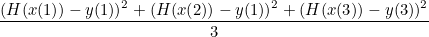
더 간단하게 표현하자면
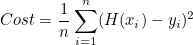
이렇게도 표현할 수 있다.
마지막으로, 이 식을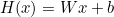
여기에 대입해주면
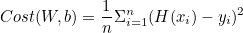
ㅤ
짜쟌-
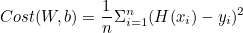
W, b에 대한 함수가 된다.
ㅤ
이 함수는 또한
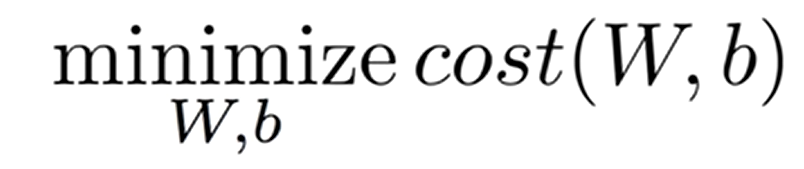
이렇게 정리할 수 있다.
ㅤ
ㅤ
ㅤ
Const function
Cost function은 머신러닝 모델을 학습하는 과정에서 최적화하려는 목표 함수,
학습된 모델의 예측값과 실제 값 사이의 오차를 나타낸다.
이 함수는 주로 모델의 가중치와 편향을 조정하여 오차를 최소화하는 방향으로 학습하는데 사용된다.
Cost function은 모든 학습 데이터에 대한 평균 오차를 계산하는 것이 일반적이다.
Loss function
Loss function도 비슷한 개념으로, 학습된 모델의 예측값과 실제 값 사이의 오차를 나타내는 함수,
주로 각각의 학습 데이터 포인트에 대한 오차를 계산한다.
Loss function은 모델의 예측값과 실제 값의 차이를 계산하여 모델을 개별 데이터에 대해 평가하고, 이를 최소화하는 방향으로 학습하는데 사용된다.

