lec 03
Contents
- Linear Regression의 cost 최소화 알고리즘의 원리
- What cost(W) looks like?
- Gradient descent(경사 하강법) Algorithm
ㅤ
ㅤ
ㅤ
ㅤ
Linear Regression의 cost 최소화 알고리즘의 원리
가설은 아래와 같다.
H(x) = Wx + b
이 가설을 cost function에 대입하면 가설과 실제 데이터의 디스턴스를 구할 수 있다.
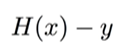
H(x) = Wx + b를 b를 뺀 식으로 변경할 수 있다.
-> H(x) = Wx
그렇다면 cost를 b를 뺀 식으로 나타낼 수 있다.
ㅤ
ㅤ
ㅤ
ㅤ
What cost(W) looks like?
그럼 이제 아래의 데이터를 보고, W = 1, 0, 2 일 때, cost(W)의 값을 구해보자.
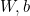
데이터는 아래와 같다.
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
- W = 1, cost(W) = ?
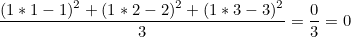
cost(W) = 0
- W = 3, cost(W) = ?
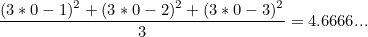
cost(W) = 4.6
- W = 2, cost(W) = ?
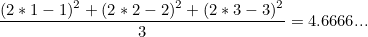
cost(W) = 4.6
이런식으로 각각의 w, y값을 함수에 대입하여 풀어준다.
ㅤ
ㅤ
cost(W)의 함수를 사용하면
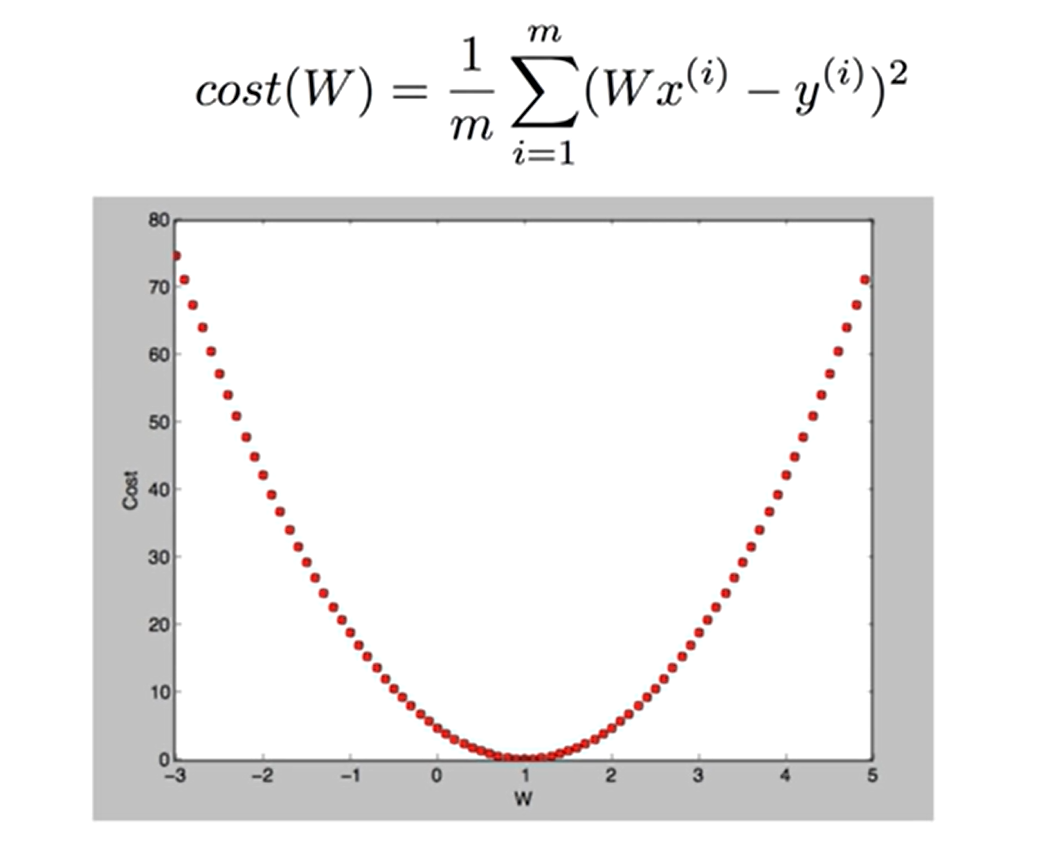
이렇게 그래프를 나타낼 수 있다.
위의 그래프는 Gredient descent Algorithm의, 쉽게말해 경사도를 나타낸 것이다.
이는 하나의 최솟값을 구하기 위해 나타난다.
ㅤ
ㅤ
ㅤ
ㅤ
Gradient descent(경사 하강법) Algorithm
- 함수의 최솟값(또는 최댓값)을 찾기 위한 최적화 알고리즘 중 하나
ㅤ
미분을 사용해 cost를 작게 만드는 W를 찾게해준다.
한마디로 새로운 W가 생성될 때 마다 업데이트 되면서 미분값이 점으로 찍히는 것이다.
식은 다음과 같다.
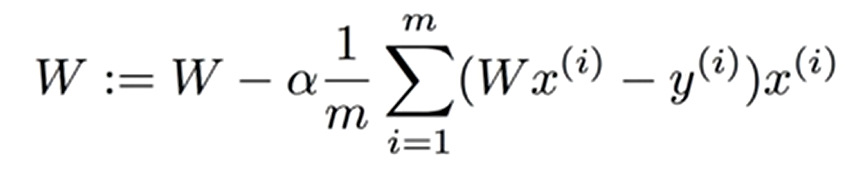
Gradient Descent는 주어진 함수가 볼록(convex)하고 미분 가능해야 최적화에 효과적으로 적용할 수 있다.
ㅤ
ㅤ
ㅤ
ㅤ
주의 주의
코드로 구현하고 끝나는 것이 아니라
Cost function(W,b)를 3차원 그래프로 표현해서 모양을 확인해야한다.
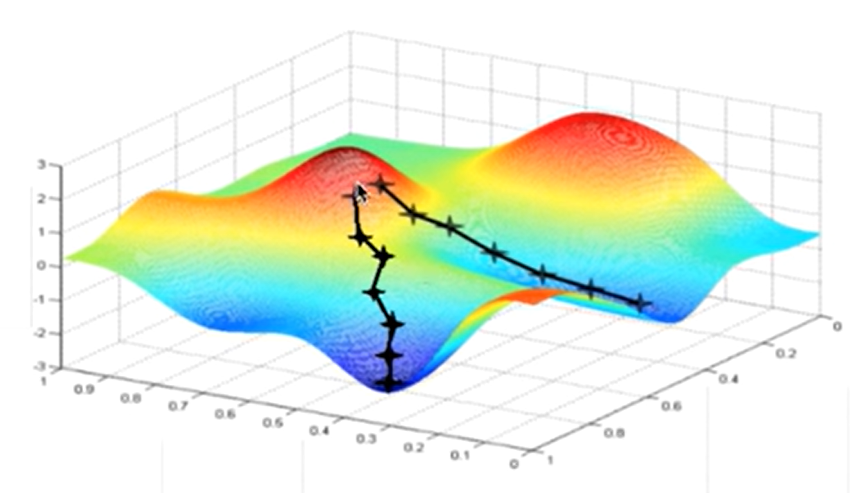
위와 같이 모양이 울긋불긋하면 안된다.
최솟값이 여러개로 나와 여러개의 길 중 하나의 길로 빠지기 때문에 최적화가 되지않아 동작을 잘 할 수 있기 때문이다.
ㅤ
따라서 아래의 모양이 잘 나오는지 확인해줘야한다.
그래야 최적의 최솟값을 찾을 수 있기 때문이다.
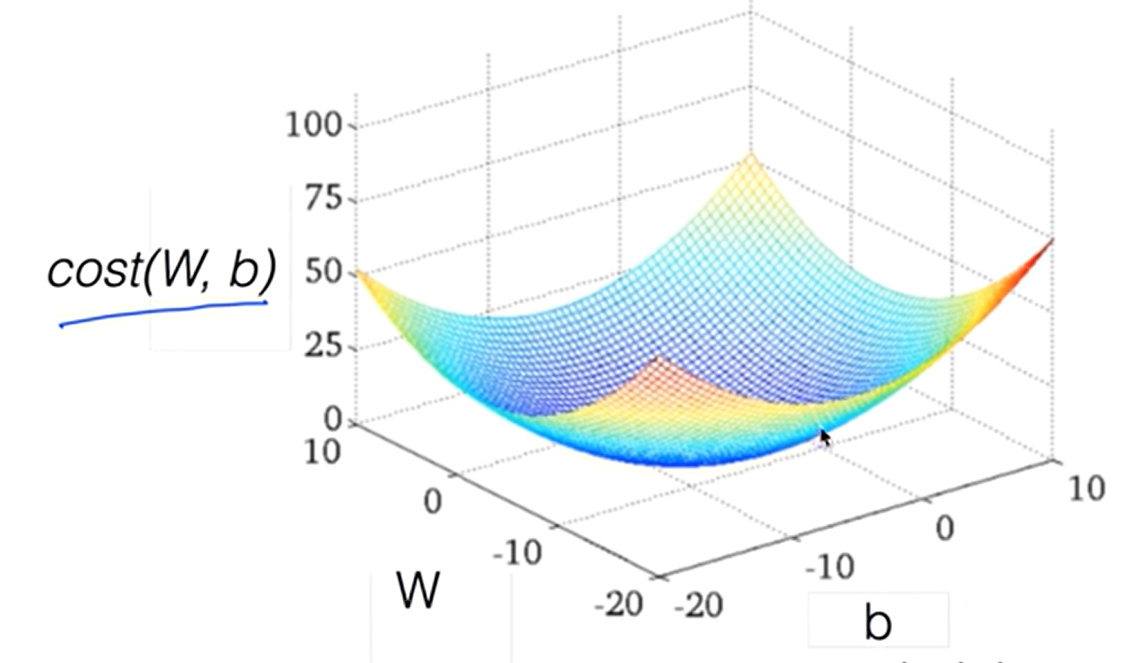
ㅤ
ㅤ
경사 하강법
장점
- 간단하고 직관적인 구현 가능
- 빠른 수렴과 확장성
단점
- 초기값에 민감하다.
- 학습률 선택 어려움
특징
- 함수가 미분이어야한다.