lec 04
Contents
-
Review
-
The number of inputs
- regression using one input (x)
- regression using Several input (x)
-
Hypothesis using matrix
-
Hypothesis using matrix
-
Instance
-
Rules of the Matrix
ㅤ
-
ㅤ
ㅤ
ㅤ
review
- Hypothesis (가설)
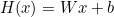
-
Cost function (비용 함수)
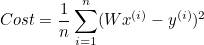
가설과 실제 데이터의 디스턴스 구하기
-
Gradient descent algotithm (경사 하강법)
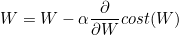
cost를 최적화하는 W, b 찾는다.
ㅤ
ㅤ
ㅤ
The number of inputsㅤ
regression using one input (x)
(입력값이 하나일 때,)
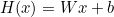
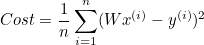
ㅤ
ㅤ
regression using Several input (x)
(입력이 여러개일 때,)
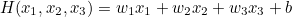
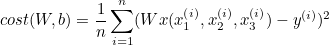
문제점
입력 값이 더더욱 많아지면 하나하나 대입하고 찾기 힘들다. (비효율적)
-> 그럴 땐 Matrix(행렬)을 사용하면 된다.
ㅤ
ㅤ
ㅤ
ㅤ
Hypothesis using matrix
Hypothesis using matrix
Matrix (행렬)
행렬은 x값이 많을 때 생겨나는 비효율적인 문제를 해결할 수 있다.
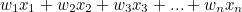
의 식을 matrix를 활용해
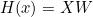
로 바꿔줄 수 있다.
예를 들어,
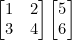
의 데이터가 있다고 할 때,
1 x 5 + 2 x 6 = 17
3 x 5 + 4 x 6 = 39 로
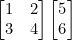
의 값이 나오는 것을 알 수 있다.
ㅤ
ㅤ
ㅤ
ㅤ
Instance
위에서는 Input값이 많은 데이터의 가설을 세우는 법을 알아보았다.
그렇다면 Instance가 많은 데이터의 가설은 어떻게 세울까?
Instan는 쉽게 말해 데이터의 행을 말한다.
아래의 식을 사용하면 인스턴스가 많을 때도 W는 변함이 없기에 똑같이 matrix를 활용해 쉽게 구할 수 있다.
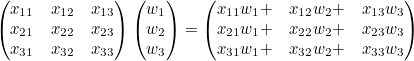
ㅤ
ㅤ
ㅤ
ㅤ
Rules of the Matrix
matrix에는 한가지 규칙이 있다.
아래의 데이터를 예로 들어보자.
[5, 3] * [3, 1] = [5, 1]
- 첫 번째 matrix의 열 부분과, 두 번째 matrix의 행 부분의 숫자가 같다.
- 첫 번째 matrix의 행 부분과, 두 번째 matrix의 열 부분의 숫자가 같다.
그럼 이 규칙으로 문제를 풀어보자.
[4, 5] * [a, b] = [4, 2]
의 데이터에서 a와 b를 구해보자.
위의 규칙을 활용하면
4 = 4
5 = a
b = 2 로
a = 5, b = 2인 것을 알 수 있다.

