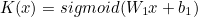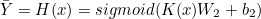lec 09-1

Contents

• XOR using NN
  • Neural Net
  • Forward propagation
  • NN

ㅤ

ㅤ

ㅤ

앞에서 정리했듯이, 하나의 유닛으로는 절대 XOR 문제를 풀 수 없다는 것이 수학적으로 증명되어 많은 연구자들에게 큰 절망을 안겨주었다.

하나가 아니라 여러개의 유닛을 사용하면 문제를 풀 수 있다는 얘기가 나왔지만,
합치는 것은 가능하지만 복잡한 네트워크 안에 들어있는 W, b를 학습시키는 것은 불가능하다고 했다.

ㅤ

ㅤ

ㅤ

ㅤ

XOR using NN

(NN으로 XOR 학습이 가능할까?)

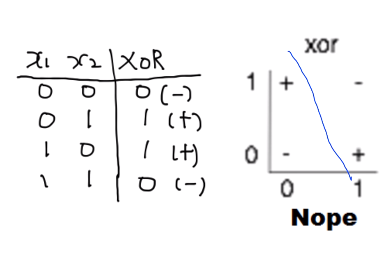
+ -를 정확하게 구분할 수 있는 선을 찾을 수 없다는 것이 문제이다.

ㅤ

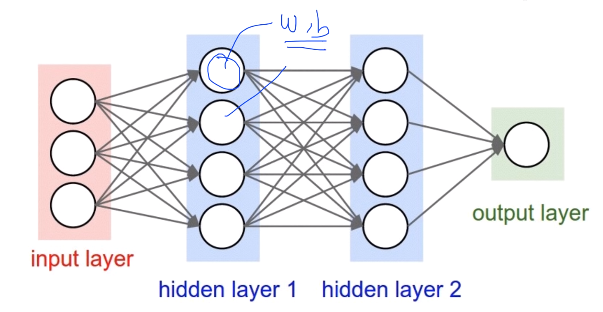
Neural Net

2개의 Input과 1개의 Output, 앞의 Sigmoid, 연산은 Wx+b로 계산한다.

앞에서 보았던 아래 그림과 똑같다.

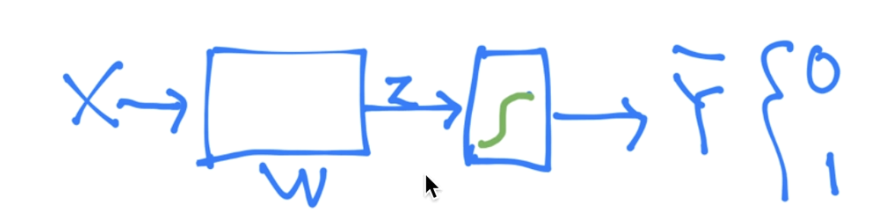
이것을 총 3개 만들어서 계산해주면 된다.

앞에서 배웠던 행렬 등을 이용해 계산해보자.

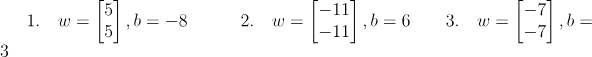
x1	x2	y1	y2	XOR
0	0
0	1
1	0
1	1

ㅤ

ㅤ

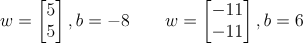
위의 식을 각각 y1, y2로 놓고 계산하면,

ㅤ

ㅤ

으로, -8은 0과 가까우니 0, 6은 1과 가까우니 1로 바꾸어
y1 = 0, y2 = 1이 된다.

XOR도 마찬가지로 위와 같은 방법으로 계산해주면 아래와 같은 결과가 나온다.

x1	x2	y1	y2	XOR
0	0	0	1	0
0	1	0	0	1
1	0	0	0	1
1	1	1	0	0

ㅤ

ㅤ

Forward propagation

이것을 하나로 뭉쳐서 그려보면 아래와 같다.

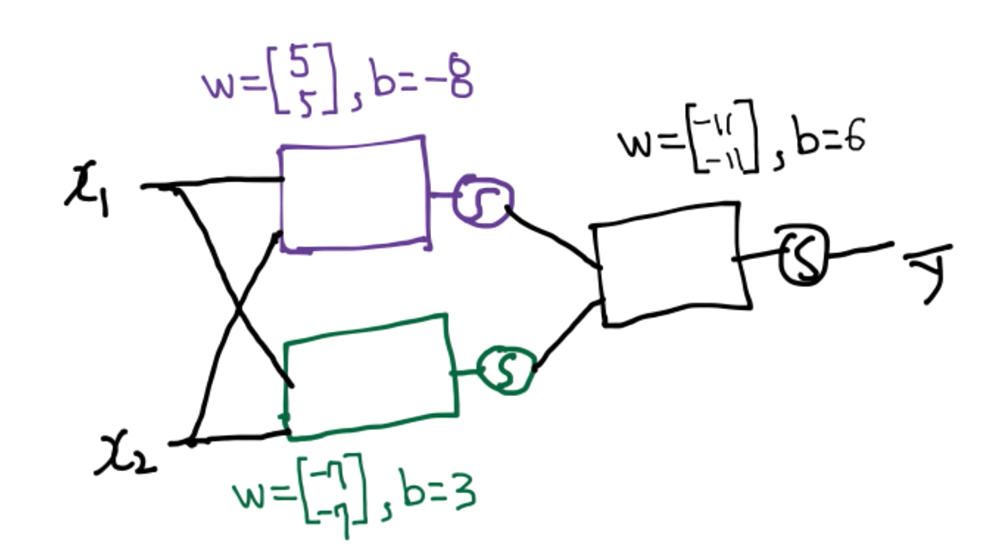
• 사각형 하나를 gate, perceptron 혹은 unit이라고 부른다.

그렇다면 위에서의 W, b 조합이 아닌, XOR이 가능한 다른 W, b 조합은 없을까?

ㅤ

ㅤ

NN

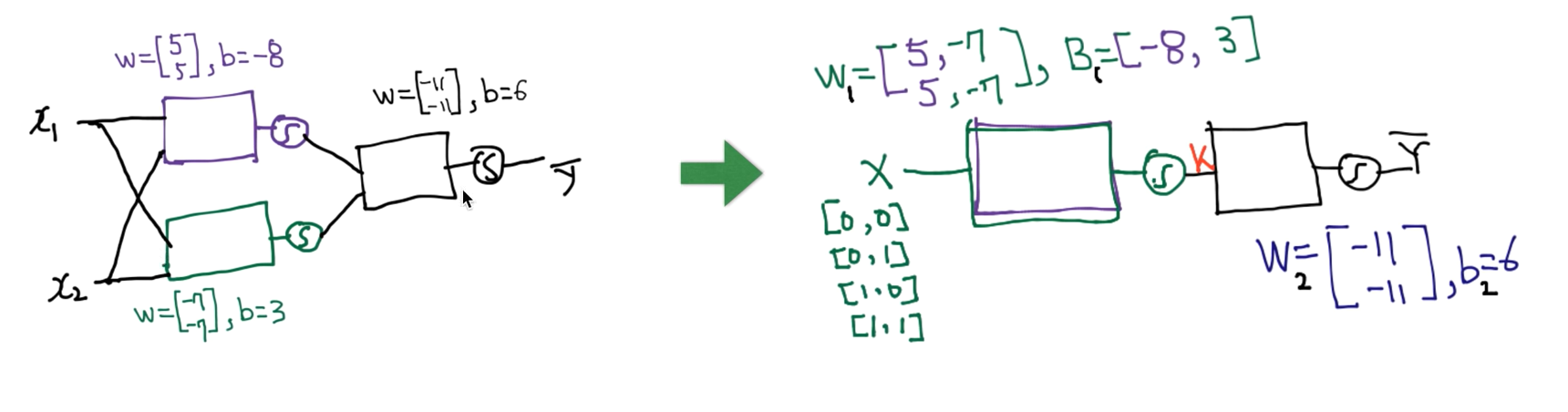
행렬 형태를 바꾸어 새로운 W, b의 조합을 만들 수 있다.

수식으로 표현하면 다음과 같다.