lec 09-2

Contents

• W, b값을 어떻게 자동적으로 학습시킬 수 있을까??
• Back propagation (chain rule 합성 함수)
  • 미분값의 의미
• Sigmoid

ㅤ

ㅤ

ㅤ

ㅤ

W, b값을 어떻게 자동적으로 학습시킬 수 있을까??

Graient descent 알고리즘를 사용하면 학습시킬 수 있다.

이 알고리즘의 구현을 위해서는 어떤 점에서의 미분값(기울기)이 필요하다.

하지만 NN으로 갈 수록 미분값이 복잡해졌는데, 이를 Back propagation 알고리즘이 해결해주었다.

ㅤ

ㅤ

ㅤ

ㅤ

Back propagation (chain rule 합성 함수)

• 출력값, 예측값을 비교하여 나온 에러를 뒤에서부터 앞으로 전달하여 미분값과 어떤 것을 조정할 지 알려주는 것

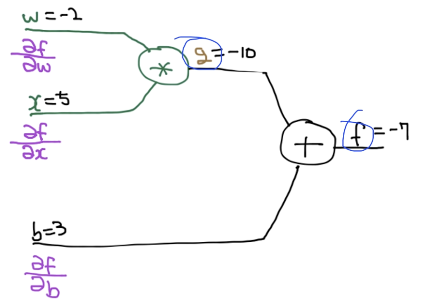
이 그래프를 통해 W, x, b가 f에 미치는 영향을 알아볼 수 있다.

두 가지 방법이 있는데,
첫번째 방법은 forward propagation이다.
forward는실제 어떤 학습 데이터의 값을 가져와서 입력한다.

앞에서 뒤로 가는 식만 계산해주면 되는데, g = Wx, f = g + b이기 때문에
g = -10, f = -10 + 3 = -7이다.

두번째 방법은 backward이다.
back은 forward와 반대로 뒤에서부터 앞으로 미분하면서 온다.
따라서 chain rule를 사용할 수 있다.

chain rule를 사용하기 위해 미분을 시켜주면,

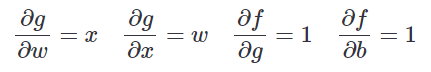
와 같이 정리할 수 있다.

이것을 식에 적용시키면
정답은 다음과 같이 나온다.

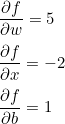
ㅤ

ㅤ

미분값의 의미

예를 들어 b가 1이면 f와의 비는 1:1이다.
f에 대한 w의 미분 값 5는 f와 1:5라는 의미로, w가 5배 증가하면 f도 5배 바례하게 증가한다.

ㅤ

ㅤ

ㅤ

ㅤ

Sigmoid

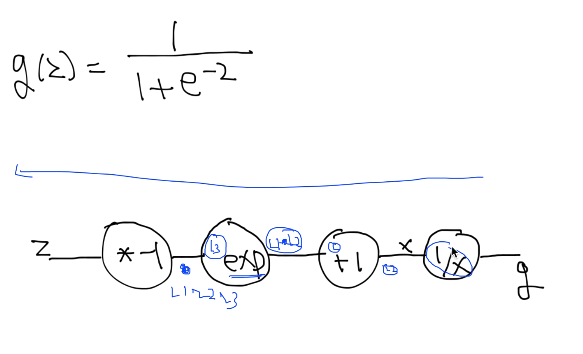
chain rule를 사용해 Sigmoid 미분을 해주면,
그림과 같이
1/x의 미분값에 +1한 것을 미분하고, 그 뒤의 미분값과 곱하고, 그 결과값을 그 뒤의 미분값과 곱하고...
이런식으로 반복해주면 Sigmoid 미분값을 구한 수 있다.
(처음 미분값만 알고있다면 가능하다!!)