빅데이터 시대에서 "빅(Big)"은 관측치가 매우 많아지는 것 뿐만 아니라 데이터의 차원이 커지는 것을 동시에 의미하며 흔히 관측치가 많아지는 것보다 변수가 커지는 것이 더 문제가 될 것이다. 그 이유는 차원이 커지면 데이터 공간을 설명하기 위해서는 데이터를 매우 많이 필요로 해진다. 이를 "차원의 저주"라고 부르는데 그에 대해서 알아보고 고차원 데이터를 다룰때 생기는 현상에 대해서 알아본다.

---

고차원 데이터(High-dimensional data)

고차원 데이터란?

흔히 말하는 고차원의 데이터는 변수(혹은 피쳐(feature))의 수$(p)$가 매우 큰 데이터를 의미한다. 단순하게 생각하면 관측치를 설명하는 변수의 수가 많다는 것은 데이터에 대한 정보량이 그만큼 많다는 것을 의미하므로 데이터 분석 측면에서 긍정적으로 생각할 수 있다. 그리고 데이터분석의 결과 역시 좋을 것으로 기대할 수 있다.

하지만 실제로 고차원 데이터는 시각화를 통한 개괄적인 데이터의 관계를 파악하기 쉽지 않으며 저차원의 데이터 분석방법을 그래도 사용하기에는 적합하지 않아서 다루기 어렵다.

쉽게 접할 수 있는 고차원 데이터는 매우 다양하다.

• Microarray dataset: 대표적인 고차원의 테이블 형식의 데이터로 feature 수가 데이터의 수보다 많은 경우가 많음
• Image dataset: 하나의 pixel이 변수가 되어서 $(\text{height} \times \text{width} \times \text{channel})$차원의 데이터
• Text dataset: 작업마다 다르겠지만 단어가 변수가 되어서 단어의 수만큼의 차원을 가지도록 구성된 데이터

단어 혹은 연어들을 사용한 데이터셋의 word cloud 시각화 모습, 그림 출처: ICML Beijing

데이터 공간의 확장

차원이 커지면서 생기는 현상에 대해서 간단한 예시를 통해 먼저 알아보자.

1. 0 또는 1을 가지는 이진변수(binary variable)가 하나 있는 경우, 우리가 고려해야하는 경우의 수는 $\{0, 1\}$로 2개이다.
2. 이진변수가 하나 추가되면 고려해야하는 경우의 수는 $\{(0,0), (1, 0), (0, 1), (1,1)\}$로 총 $2^2=4$개이다.
3. 이진변수가 $d$개 추가된다면 $2^d$개의 경우의 수가 존재하며 결과적으로 차원이 커짐에 따라 지수적으로 경우의 수가 증가한다.

지수적으로 증가하는 것은 매우 빠르게 증가하는 것을 의미한다. 변수가 많아지면 즉, 데이터의 차원이 커질수록 고려해야하는 경우가 매우 빠르게 많아지는 것이다. 이러한 현상을 combination explosion이라고 부른다.

Combination explosion이 발생하는 문제로는 multilabel classificaion이 있다. label의 종류가 많아지면 고려해야하는 label의 조합이 많아져서 복잡한 문제가 된다.

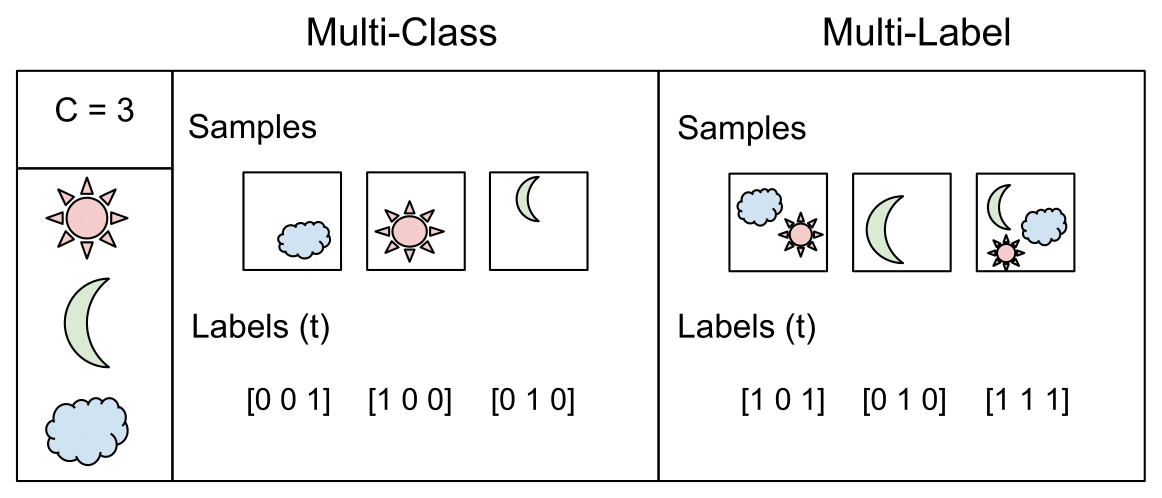그림 출처: Raúl Gómez blog

---

고차원 데이터를 다루는 경우 발생하는 문제점

차원의 저주(Curse of dimensionality)

위에서 차원이 커질수록 데이터 공간의 크기는 지수적으로 커지는 것을 확인했는데 확장된 공간을 채우기 위해서 필요한 데이터의 수는 어떻게 변할까? 직관적으로 지수적으로 증가하는 것을 기대할 수 있다.

• $[0 ,1]$ 구간의 수직선 상에서 거리가 $0.01$ 이하로 샘플링하려면 $10^2=100$개의 균일하게 퍼져있는 점이 필요하다.
• $[0 ,1] \times [0 ,1]$ 사각형 공간에서 거리가 $0.01$ 이하로 샘플링하려면 $10^4=10000$개의 균일하게 퍼져있는 점이 필요하다.

필요한 데이터의 지수적인 증가는 현실적으로 처리하기가 어렵다. 이러한 불가피한 경우를 차원의 저주(Curse of dimensionality)라고 부른다.

그림 출처: KDD 2014 tutorial, Yoshua Bengio

유클리디언 거리(Euclidean distance)

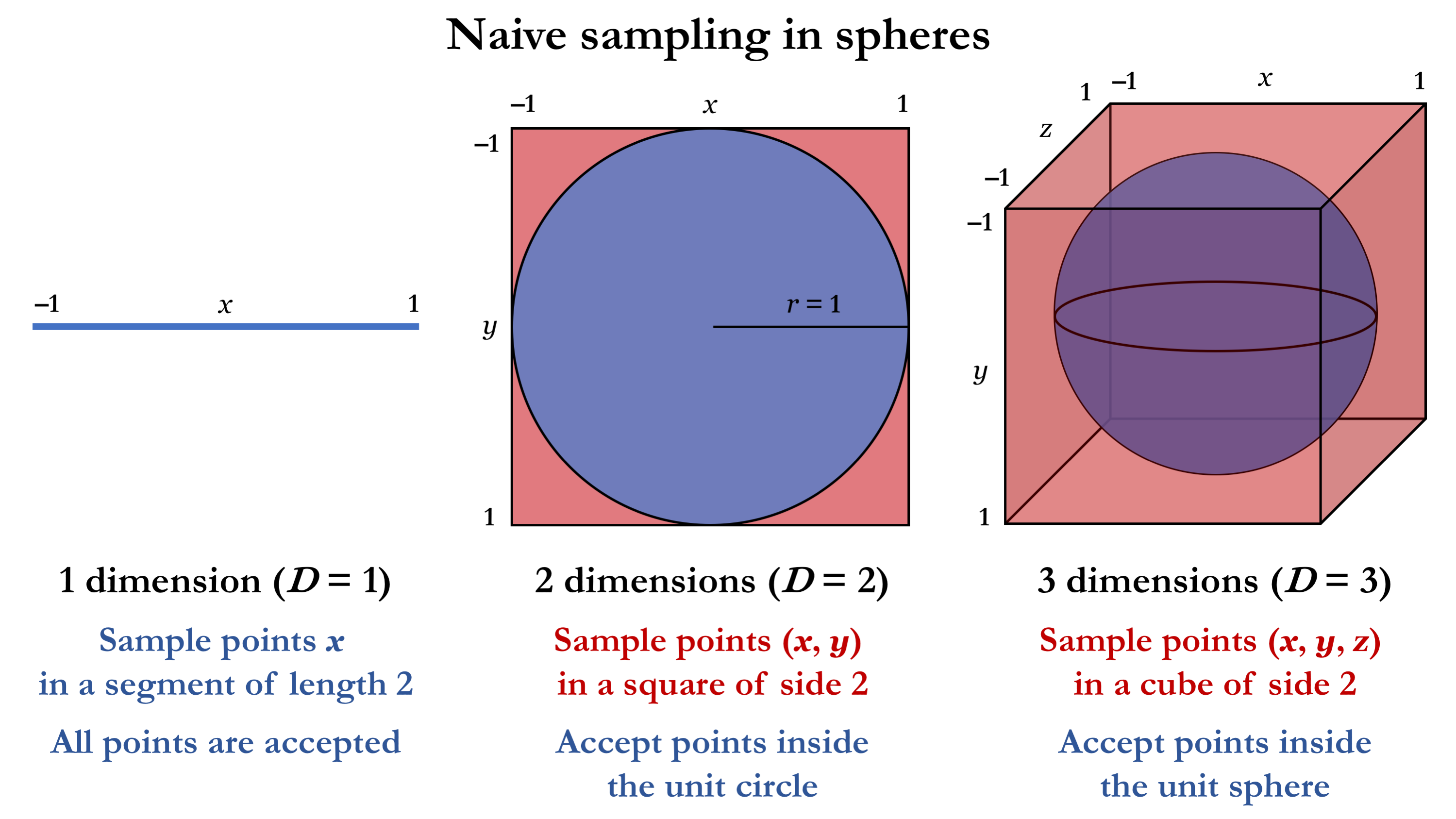그림 출처: Adrian Baez-Ortega blog

• 사각형의 한변의 길이가 $2$이면 사각형의 넓이는 $4$, 내접하는 원의 넓이는 $\pi$ 그리고 사각형과 원의 넓이 비율은 $\frac{\pi}{4} \approx 0.785$
• 정육면체의 한변의 길이가 $2$이면 부피는 $8$, 내접하는 구의 부피는 $\frac{4}{3}\pi$ 그리고 부피의 비율은 $\frac{\pi}{6} \approx 0.524 < 0.785$

수학적으로 차원이 무한히 커진다면 초입방체(hypercube)와 초구(hypersphere)의 부피 비율은 $0$으로 수렴한다. 즉, 다차원 공간에서 대부분의 데이터는 데이터 공간의 표면에 가깝게 위치한다.

"무한한 차원의 오렌지의 껍질을 벗기면 아무것도 남지않는다. 껍질에 모든 질량이 다 포함되어 있기 때문이다. "

이번에는 다른 예시를 생각해보자.

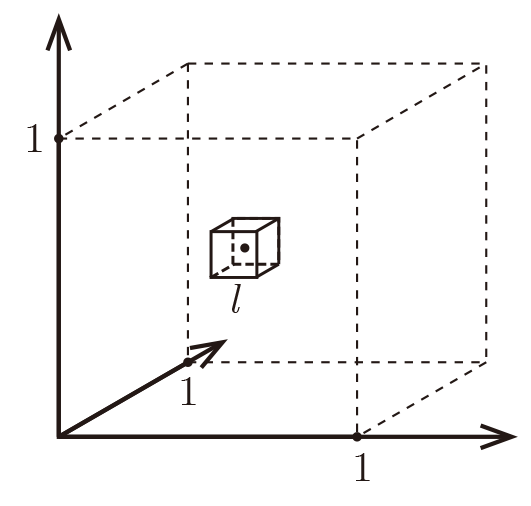그림 출처: Cornell 대학교 lecture note

위와 같은 $3$차원 공간에서 길이가 $1$인 정육면체가 있다고 생각하자. 그리고 데이터들은 정육면체 안에서 균일하게(uniformly) 흩어져있다. 그렇다면 한점에서 가까운 점 $10$개를 포함하는 작은 정육면체를 생각할 수 있다. 그렇다면 그 작은 정육면체$(l)$의 길이는 얼마가 될까?

• $l^3 \approx \frac{10}{1000} \rightarrow l \approx (\frac{10}{1000})^{1/3} \approx 0.215$

위의 식이 직관적으로 이해할 수 있다. 만약 이해가 되지 않는다면 $\frac{l^3}{1^3} \approx \frac{10}{1000}$으로 생각해보자. 균일하게 퍼져있으므로 전체 부피 $1^3$에는 $1000$개의 데이터가 모두 있을것이고 $l^3$를 가지는 작은 정육면체에는 $10$개가 있을테니 $l$를 위와 같이 비례식을 생각할 수 있다.

이제 식에서 차원을 $3$차원보다 큰 상황을 생각해보자.

• $l^d \approx \frac{10}{1000} \rightarrow l \approx (\frac{10}{1000})^{1/d}$

여기서 만약 $d$가 $1000$이라면 $l \approx 0.995$로 작은 정육면체가 아니라 전체 공간과 거의 비슷한 크기로 커져야 가까운 점 $10$개를 포함한다. 나머지 $990$개의 점들은 전체 공간에서 길이가 $0.995$인 정육면체를 제외한 껍질에 있을 것이다. 그렇다면 $10$개의 점과 $990$개의 점들은 정말 구별될정도로 가깝고 멀다라고 할 수 있을까? 아니다. 차원이 커질수록 데이터들간의 거리가 서로 멀어지면서 가깝고 멀다라는 거리의 개념이 약해지게 된다. 단순하게 생각하더라도 2차원에서 데이터의 거리는 $\sqrt{\Delta x^2 + \Delta y^2}$라고 한다면 3차원에서는 $\sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2}$로 적어도 2차원인 경우보다 클 확률이 높다. 하지만 우리가 3차원 이상의 공간에서 데이터간의 거리가 동일하게 멀어진다라는 것을 직관적으로 받아들이기는 쉽지 않다. 아래에 실제로 실험에서 데이터쌍의 거리를 구한 자료를 통해 받아들이고 넘어가자.

그림 출처: Cornell 대학교 lecture note

고차원 공간에서 유클리디언 거리 기반 알고리즘

위의 결과에서 고차원 공간에서 거리의 개념이 약해지면서 k-nearest neighbor 알고리즘이나 k-means clustering와 같은 거리 기반의 알고리즘에서 문제가 발생한다. 고차원 상에서는 데이터들간의 거리는 동일하게 점점 멀어지게 된다. 따라서 가까운 이웃과 먼 데이터의 구분이 어려워지고 $k$개의 이웃에 성질이 다른 데이터들이 포함되기 때문에 성능이 저하된다. 아래의 그림은 각 차원에서 1000개의 sample을 생성했을 때, sample간의 거리의 비율을 나타낸 그래프이다. 차원이 커질수록 데이터간의 거리는 매우 좊은 구간에 집중되면서 거리의 의미가 없어진다. 실제로 고차원의 데이터를 다루는 경우에 유클리디언 거리 기반의 알고리즘으로 군집화를 한다면 성능이 만족스럽지 않은 이유이다.

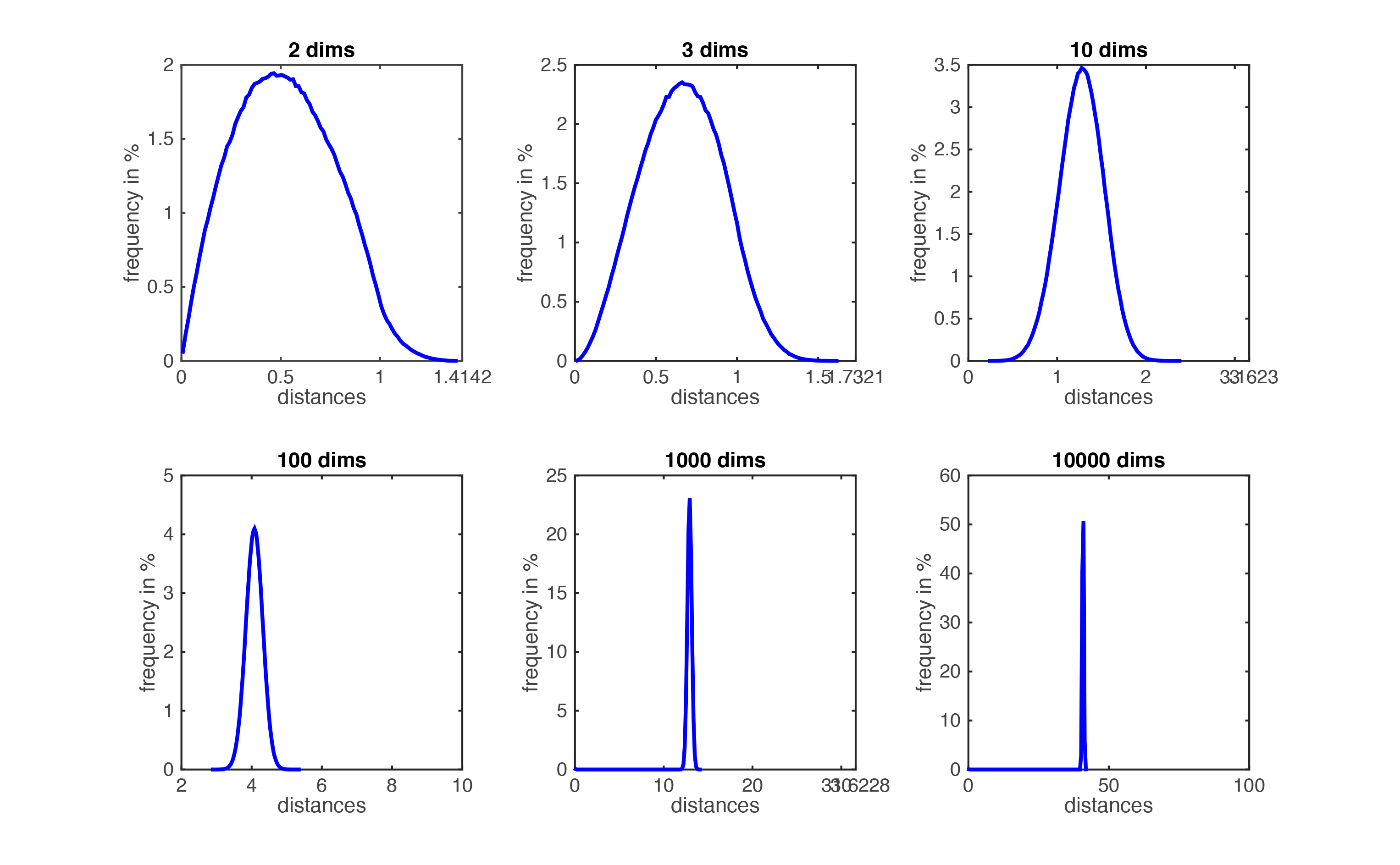그림 출처: Cornell 대학교 lecture note

고차원 데이터를 다룰 때 생기는 문제점에 대해서 정리를 해보았다. 실제 데이터에서도 저런 문제가 발생할텐데 어떻게 해결을 하는가?라는 질문이 생긴다. 해답은 "고차원의 데이터가 있는 공간이 실제로는 저차원의 공간이다"라는 생각을 가지고 저차원의 공간을 학습하게 된다. 그 저차원의 공간을 영어로는 manifold라고 부르며 그런 학습기법은 manifold learning이라고 부른다. 쉽게 생각해보면 범인 몽타주를 그릴 때 범인의 흑백 스케일부터 눈코입의 정확한 위치 등의 정보를 사용하지 않는다. 얼굴의 형태는 ..., 코는 ..., 눈썹은 ..., 등의 몇몇 정보를 활용하여 몽타주를 그린다. 이렇듯 몽타주 자체는 매우 많은 pixel을 가지는 고차원 데이터지만 몽타주를 표현하는 데이터는 몇 가지 정보만으로도 이해할 수 있다. 이러한 아이디어가 VAE(Variational Autoencoder) 등에 사용되었으며 최근에도 많이 연구가 되고 있다. 관심이 있다면 찾아보면 좋을 것 같다.