"공분산 행렬 (Covariance Matrix)"은 통계학과 선형대수학에서 중요한 개념으로, 다변량 데이터 집합에서 변수 간의 상관 관계와 분산을 나타내는 행렬이다. 공분산 행렬은 다음과 같은 목적으로 사용된다:
-
변수 간 상관 관계 분석: 공분산 행렬을 통해 다른 변수들 간의 상관 관계를 분석할 수 있다. 공분산 행렬의 요소들은 두 변수 간의 공분산을 나타내므로, 양수 값은 양의 상관 관계를 나타내고 음수 값은 음의 상관 관계를 나타낸다.
-
주성분 분석 (PCA): PCA는 다변량 데이터의 차원 축소를 위해 주로 사용된다. 공분산 행렬을 이용하여 데이터의 주성분(고유 벡터)을 추출하고, 이러한 주성분을 이용하여 데이터를 저차원 공간으로 변환한다.
공분산 행렬의 요소 (i, j)는 변수 i와 변수 j 간의 공분산을 나타내며, 공분산은 두 변수가 함께 어떻게 변하는지를 측정하는 지표이다. 공분산 행렬은 대칭 행렬이며 주대각선에는 각 변수의 분산이 위치하고, 나머지 항목에는 변수 간의 공분산이 위치한다.
다음은 공분산 행렬의 간단한 예를 보여준다:
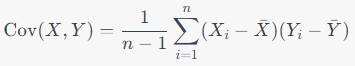
여기서,

공분산 행렬은 다변량 통계 및 다변량 데이터 분석에서 중요한 도구로 사용되며, 변수 간의 관계를 파악하고 데이터를 변환하거나 축소하는 데 도움을 준다.
