Embarrassingly Shallow Autoencoders for Sparse Data

한줄요약
hidden layer를 아예 사용하지 않고 shallow하게, closed-form으로, self-similarity를 없애고 추천시스템 모델을 만들어봤더니 sparse에도 강하고 다양한 최첨단 모델보다 성능도 뛰어났다!
0. ABSTRACT
- linear model이다.
- closed-form solution이다.
- non-linear model보다 성능이 뛰어나다.
1. INTRODUCTION
computer vision과는 달리 collaborative filtering은 hidden layer를 적게 사용하는 것이 오히려 성능이 더 좋다는 것이 밝혀졌다. 그래서 이 논문의 저자는 극단적으로 hidden layer가 아예 없는 linear한 모델을 만들었다.
'E'mbarrassingly 'S'hallow 'A'uto'E'ncoders의 약자 -> ESAE를 reverse해서 -> EASE
(약자를 굳이 reverse를 하여 ease로 만들어서 "쉬운" 뭐 이런 뜻도 내포하게 하려는 의도인 것 같다...)
(모델의 이름을 EASE라고 했으니 나도 이제부터 EASE라고 쓰겠다)
결론적으로 publicly available data-sets(MovieLens-20M, Netflix, MSD)에서 EASE가 neighborhood-based 접근법 뿐만아니라 다양한 deep, non-linear, probabilistic models의 성능도 능가한다.
2. MODEL DEFINITION
데이터 설명
- X -> U x I 행렬 (input data, binary)
- B -> I x I 행렬 (model, weight)
- S -> U x I 행렬 (predict)
X는 user x item으로 binary 되어있는 행렬이고, B는 우리가 closed-form으로 훈련하는 모델이고, S는 X·B를 하여 나온 predict 행렬이다.
3. MODEL TRAINING
우리는 B라는 weight-matrix를 closed-form으로 훈련시키면 된다.

간단하게 설명하면 X와 X·B의 차이가 최소가 되는 B를 구해주면 된다.
(뒤에 L2-norm regularization이 있긴하다, 람다는 model에서 유일한 하이퍼파라미터)
그리고 정말정말 중요한 것이 diag(B)=0 이라는 것이다. 뒤에 가서도 다시 한 번 설명하겠지만 이 논문에서 제일 중요한 포인트이다. X와 X·B가 최소가 되는 B를 diag(B)=0이라는 조건 없이 구하면 B=I(단위행렬)이다. 우리는 predict matrix인 S를 알고 싶어서 B라는 weight-matrix를 훈련시키는 것인데, B=I(단위행렬)라고 구해버리면 predict matrix인 S는 input data인 X와 같아진다. B=I(단위행렬)이면 아무 의미가 없어진다는 말이다. 그렇기 때문에 diag(B)=0라는 조건이 필요하고 이것이 self-similarity를 없애준다.
closed-form 계산 과정
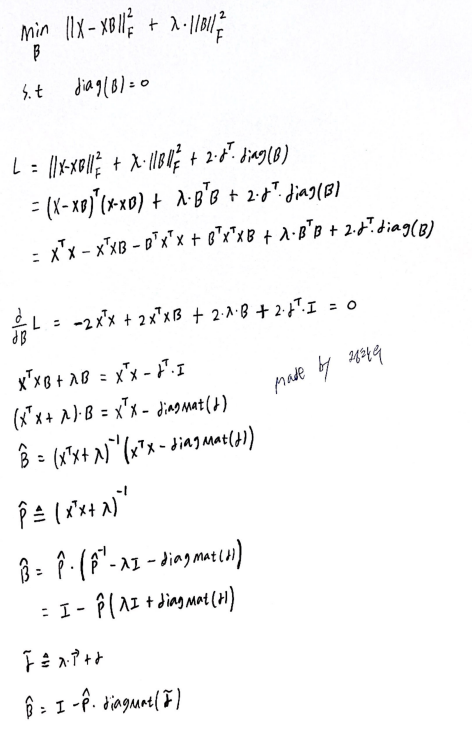
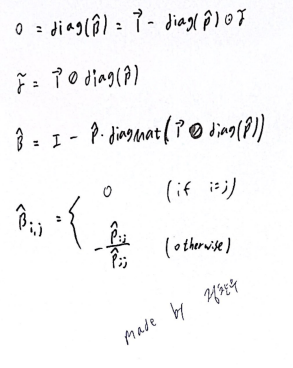
4. RELATED WORK
- Deep Learning and Autoencoders
- Slim and Variants
- Neighborhood-based Approaches
5. EXPERIMENTS
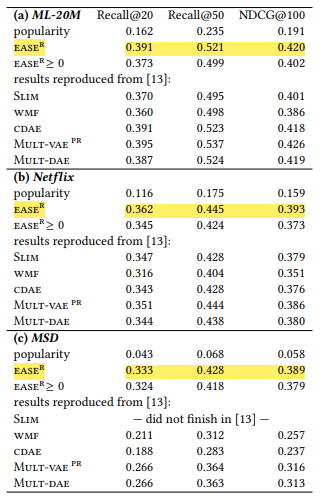
Netflix와 MSD에서 SOTA를 기록하였다. 특히 MSD에서는 다른 모델과 비교했을 때 엄청난 성능을 보여준다.
6. CONCLUSIONS
- weights가 음수 값이 나오도록 허용하는 것이 성능 향상을 위해 필요하다.(유사성 외에도 항목 간의 차이점을 학습할 수 있으므로)
- 성능이 neighborhood-based 접근법 뿐만아니라 deep non-linear을 포함한 다양한 최점단 접근법보다 동등하거나 우수하다.
그리고 이 논문의 제목인 Embarrassingly Shallow Autoencoders for Sparse Data에서 마지막에 "for Sparse Data"가 붙는 이유를 아래 문장에서 설명해준다.
This suggests that models where the self-similarity of items is constrained to zero may be more effective on sparse data than model architectures based on hidden layers with limited capacity.
MovieLens-20M, Netflix, MSD 중에서 MSD가 가장 sparse한 것으로 알려져 있는데, MSD에서 EASE가 다른 최첨단 모델보다 폭발적인 성능을 보여주는 이유가 여기에 있지 않을까 추측해본다.
code
official code가 있긴 있는데 데이터 전처리 파트는 없어서 데이터 전처리에서 고생을 했다.
내가 실수했던 부분
- unique item으로 해야함
- test user는 X 행렬에서 빼줘야함