오늘 배운 것
데이터 이해 단계
EDA, CDA의 데이터 분석 단계는 크게 3가지로 나눌 수 있다.
- 개별 변수 탐색
- 가설 검증 (x -> y 관계 검증)
- 요인 간 관계 확인
데이터 분석의 가장 큰 목표는 데이터와 도메인을 보다 잘 이해하여, 새로운 인사이트를 도출하는 것이므로
엄격한 경계값에 따라 판정하거나, 복잡한 가정을 모두 지킬 필요는 없다.
도구와 가정
히스토그램, 산점도, 기초통계량, 분포표 등의 Tool은 모두 데이터 분석을 위한 도구이다.
모든 도구는 각자 해당하는 가정이 필요하다 (정규성 충족, 요인간 독립성 등등)
하지만, 데이터 이해 단계에서 아직까지는 이런 복잡한 가정을 검사하는 것 보다는, 우선 도구를 사용하고 결과를 이해하는데 집중하자.
단, 보이는 결과가 항상 옳지 않다는 것을 명심하자.
이변량 분석(숫자 vs 숫자)
시각화 : 산점도
-
두 변수 x, y에 대해 데이터가 갖는 모든 값을 그래프에 점으로 찍어 표시한 그래프이다.
-
두 숫자형 변수간의 관계를 나타낸다.
-
핵심 관점 : 두 변수의 관계가 얼마나 직선으로 설명이 되는가
-
산점도는 드물게 데이터를 요약하지 않는 그래프이다. (정보 손실이 없음)
산점도 그리기
-
산점도
plt.scatter(x축 값, y축 값)sns. scatterplot(x=x축 값, y=y축 값)
-
pairplot()
sns.pairplot(df)- seaborn이 제공하는 함수로, 데이터의 모든 변수 조합에 대해 산점도와 히스토그램을 그려서 출력한다.
- 변수가 많을수록 연산에 시간이 매우 오래걸리며, 일일히 파악하기 어렵다는 단점이 있다.
상관 분석
-
상관 분석은 두 변수 간 유의미한 관계가 있는지 수치적으로 분석하는 방법이다.
-
상관계수와 p-value를 이용한다.
상관계수(correlation coefficient)
-
변수 간 관계의 크기를 수치화하여 정량적으로 나타낸 값이다.
-
값의 범위가 -1 ~ 1로 정규화 되어있어 상관계수 간 비교가 가능하다.
-
0에 가까울수록 관계가 없음을 나타내고, 1 또는 -1에 근접할 수록 관계가 강함을 나타낸다.
상관계수의 한계
-
상관계수는 직선의 관계만 수치화 할 수 있다.
-
데이터가 여러 그룹으로 나눠진 경우에도 하나의 관계만 고려하므로 상관관계가 모든 관계를 나타낼 수 없음을 알아야 한다.
-
상관계수와 함께 반드시 산점도 등의 시각화 그래프를 눈으로 확인해야 한다.
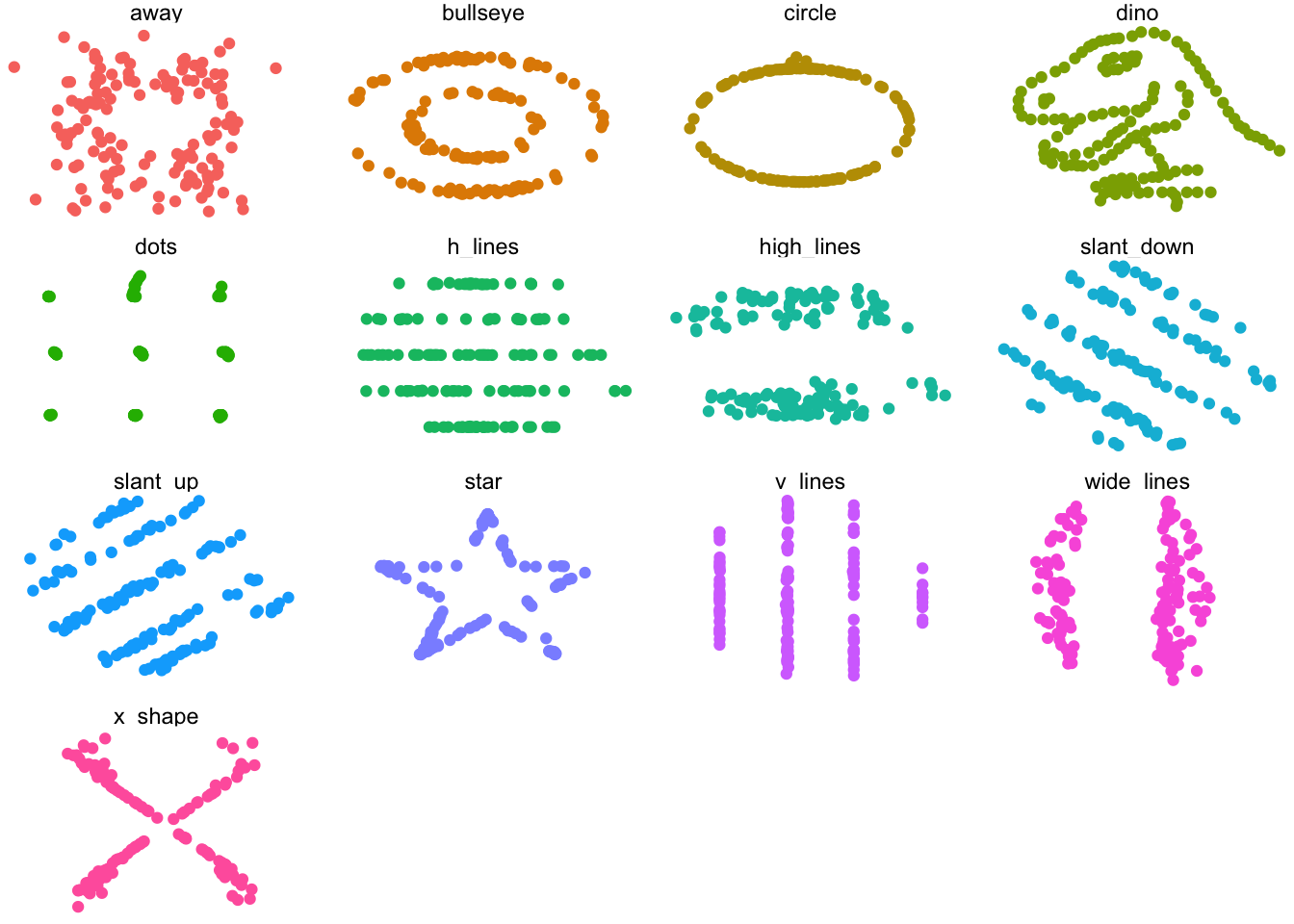
# A tibble: 13 x 6
dataset mean_x mean_y std_dev_x std_dev_y corr_x_y
1 away 54.3 47.8 16.8 26.9 -0.0641
2 bullseye 54.3 47.8 16.8 26.9 -0.0686
3 circle 54.3 47.8 16.8 26.9 -0.0683
4 dino 54.3 47.8 16.8 26.9 -0.0645
5 dots 54.3 47.8 16.8 26.9 -0.0603
6 h_lines 54.3 47.8 16.8 26.9 -0.0617
7 high_lines 54.3 47.8 16.8 26.9 -0.0685
8 slant_down 54.3 47.8 16.8 26.9 -0.0690
9 slant_up 54.3 47.8 16.8 26.9 -0.0686
10 star 54.3 47.8 16.8 26.9 -0.0630
11 v_lines 54.3 47.8 16.8 26.9 -0.0694
12 wide_lines 54.3 47.8 16.8 26.9 -0.0666
13 x_shape 54.3 47.8 16.8 26.9 -0.0656저 말도안되는 산점도의 상관계수는 모두 -0.06 정도이다.
p-value
-
상관계수 뿐 아니라 다양한 통계량(관계를 수치화 한 값)이 유의미한지 판단할 때 사용한다.
-
일반적으로 p-value < 0.05이면 관계를 수치화 한 값이 의미가 있다고 본다.
- 예를들어 상관 분석에서는 두 변수간 관계가 있다는 것으로 판단한다.
- 의료분야 등 좀 더 엄격하게 판정해야 할 경우 0.01이나 더 낮은 숫자를 기준으로 잡기도 한다.
-
주의 사항
- p-value는 데이터가 많아질수록 0에 수렴한다.
- 만약 데이터가 너무 많다면 p-value를 너무 신뢰하지 말자.
df.corr()
- 판다스가 제공하는 메서드로, 해당 데이터프레임의 모든 변수간 상관계수를 보여준다.
- p-value를 보여주지는 않으니, 꼭 따로 구해서 유효한지 확인하자.
NaN 검사
-
NaN 값이 포함된 데이터가 있으면 그래프를 그리지 못하는 경우가 많이 존재한다.
때문에 시각화에 앞서 NaN을 검사하고, 처리하는 과정이 필요하다. -
df.info
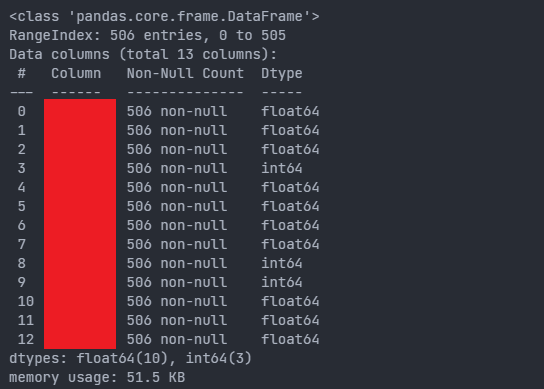
데이터프레임의 정보를 출력하는 메서드
506개의 행중에 506개의 non-null이 있으므로 NaN이 하나도 없다는 것을 알 수 있다. -
df.isna().sum()
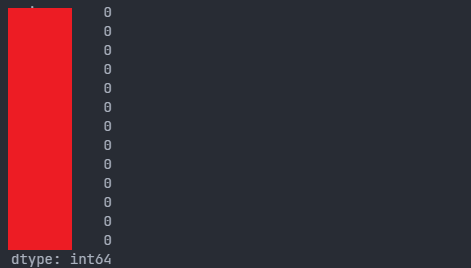
열별 NaN의 개수를 반환한다.
평균
분산, 표준편차
- 분산은 한 집단에서 값들이 평균으로 부터 얼마나 벗어나 있는지를 나타낸다.
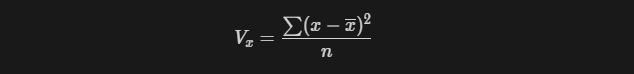
- 표준편차는 분산의 제곱근과 같다.
모집단과 표본
-
모집단
- 모집단은 조사 대상 전체를 나타낸다.
- 조사 대상을 전수조사하면 모집단의 평균인 모평균, 모분산 결과를 얻을 수 있다.
-
표본
- 시간, 비용 문제로 인해 전수조사를 할 수 없어 모집단에서 일부를 샘플링한 집단을 표본이라 한다.
- 샘플링은 반드시 무작위 추출을 해야한다 (편향 방지)
- 표본으로 부터 표본 평균, 표본 표준편차를 얻을 수 있다.
- 표본 평균은 모평균의 추정치이며, 반드시 어느정도의 오차(표준 오차)가 존재한다.
이변량 분석(범주 vs 숫자)
범주(x)와 숫자(y)를 비교할 때는 평균을 이용한다.
범주의 종류가 2개인지, 3개 이상인지에 따라 이용 가능한 도구가 달라진다.
- 귀무가설 : 범주간 차이가 없다
- 대립가설 : 범주간 차이가 있다
시각화 : sns.barplot()
-
sns.barplot(y=숫자 데이터, x=범주 데이터) -
seaborn이 제공하는 barplot 함수로 범주간 평균값을 비교할 수 있다.
-
범주별 평균값과 신뢰구간을 함께 표시해주며, 신뢰구간이 좁을 수록 오차범위가 작음을 의미한다.
- 일반적으로 데이터가 많고, 편차(분산)이 작을수록 신뢰구간이 좁아진다.
-
두 평균에 차이가 크고, 신뢰구간이 겹치지 않을 때 범주간 평균에 차이가 있다고 본다. (대립가설 채택)
수치화 : t-test
-
문법 : `spst.ttest_ind(범주1, 범주2)
-
범주가 2종류일 때 사용하며, 두 범주의 평균을 비교해 차이가 있는지를 검정한다.
-
통계량(t)은 두 그룹 간 평균의 차이 표준 오차로 나눈 값이다.
- 일단은 두 그룹 간 평균 차이 정도로만 이해하자
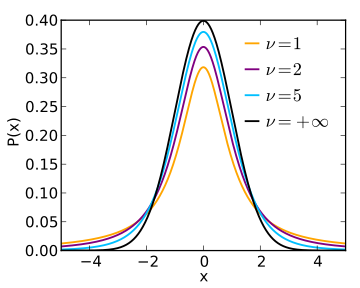
-
t분포는 데이터의 수가 많을수록 정규분포에 근사한다.
-
판정방법
- 통계량 t가 -2보다 작거나 2보다 클 때 일반적으로 차이가 있다고 판정
- p-value가 0.05보다 작을 때 일반적으로 차이가 있다고 판정
수치화 : ANOVA
-
문법 : `spst.f_oneway(범주1, 범주2, 범주3, ...)
-
범주가 3종류 이상일 때 사용하며, 범주 간 분산과 범주 내 분산을 비교하는 F검정을 이용한다.
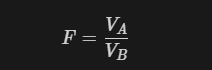
-
범주 간 분산이 클 수록, 범주 내 분산이 작을 수록 F 통계량이 커지고, 이는 범주 칸 차이가 있음을 나타낸다.
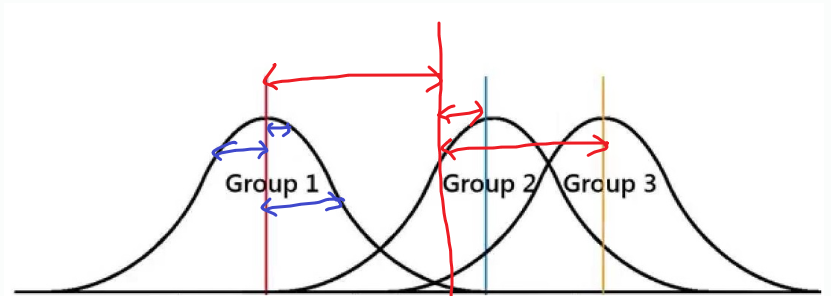
-
빨간색 선이 범주 간 분산, 파란색 선이 범주 내 분산을 나타내며, 이를 비교하여 그룹 간에 차이가 있는지 없는지를 검정한다.
-
차이가 있다 없다는 알 수 있지만, 어떤 범주끼리 차이가 있는 것인지는 알 수 없다.
- 알기 위해서는 모든 조합에 대해 일일이 t-test를 돌려야 한다.
-
판정방법
- 통계량 F가 2보다 클 때 일반적으로 차이가 있다고 판정
- p-value가 0.05보다 작을 때 일반적으로 차이가 있다고 판정

