오늘 배운 것

이변량 탐색 : 범주 -> 범주

요인 x가 범주형 데이터, 목표 y도 범주형 데이터일 때 데이터를 탐색하는 방법을 다룬다.
기본적으로 교차탭을 이용한다.

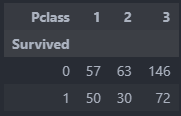
집계 : 교차표

• 교차표는 말그대로 각 요인 범주별로 빈도수를 집계한 표이다.

• pandas가 제공하는 crosstab 함수를 통해 쉽게 집계할 수 있다.

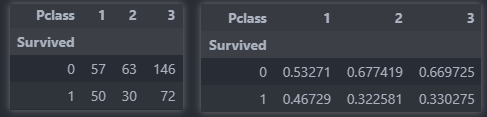
• 문법 : pd.crosstab(행 data, 열 data, normalize=?)

• normalize 옵션을 통해 빈도수 대신 비율로 결과를 출력할 수 있다.

  • normalize = columns : 각 열의 합이 1이 되도록 비율계산
  • normalize = index : 각 행의 합이 1이 되도록 비율계산
  • normalize = all : 모든 값의 합이 1이 되도록 비율계산

시각화 : mosaic plot

• statsmodels 패키지에서 제공하는 그래프로, plt의 옵션이 먹지 않는 경우가 많다.

• crosstab을 만드는 과정 없이 내부적으로 집계하여 바로 그래프를 출력해준다.

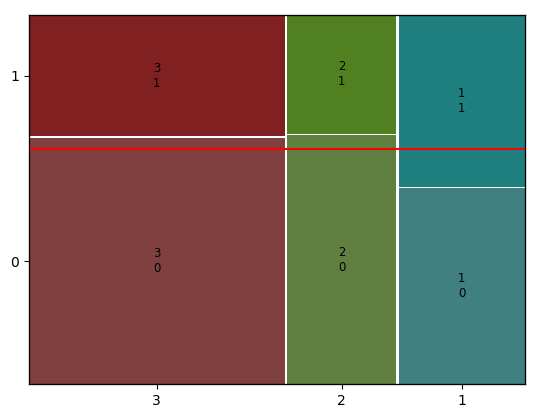
• 문법 : mosaic(데이터, [x축 범주 이름, y축 범주 이름])

  • 붉은 선은 범주의 전체 평균을 나타내며 plt.axhline을 이용해 따로 추가한다.

• 해석

  • x축에서 3, 2, 1 각 범주의 가로 길이가 비율을 나타낸다
    Pclass 3을 이용한 승객이 가장많고, 2를 이용한 승객이 가장 적다.
  • y축에서 1, 0 각 범주의 세로 길이 역시 비율을 나타낸다
    Survived가 0인(사망한) 승객이 더 많다
  • 평균선을 기준으로 2등급과 3등급을 이용한 승객은 평균보다 더 많이 사망했으며, 1등급을 이용한 승객은 평균보다 더 많이 사망했다
    -> Pclass 범주는 Survived 범주와 관계가 있다. (대립가설)

수치화 : 카이 제곱 검정 (Chi-squared test)

• 기대 빈도와 실제 관측된 빈도의 차를 이용해서 차이가 있는지를 검정하는 방법이다.

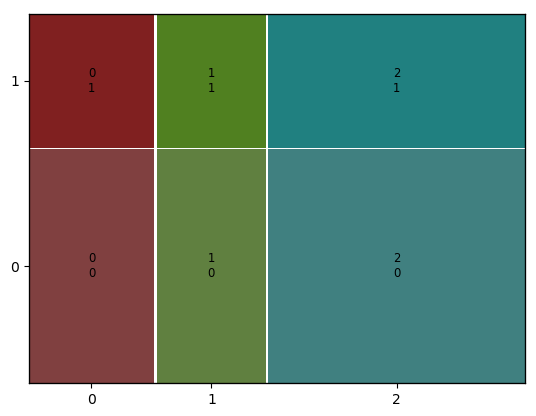
• 기대 빈도 : 귀무 가설(x 범주 간 빈도의 차이가 없다)이 참일 때 기대할 수 있는 빈도수이다.
  가령 남녀의 평균 비율이 50%, 생존율 역시 50% 라면 기대 빈도 비율은 0.25, 0.25, 0.25, 0.25가 된다.

• 기대 빈도의 빈도표를 이용해 mosaic plot을 그리면 다음과 같이 모든 범주가 동일한 비율을 갖게 된다.

• 결과 해석
  

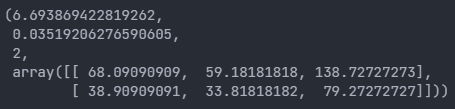
1. 검정 통계량 (6.69...)
2. p-value (0.035...)
3. 자유도 ( (n-1) * (m-1) = 2)
4. 기대빈도

• 판정
  • 통계량이 대략적으로 자유도의 2배보다 크면 차이가 있다고 판정한다.
  • p-value가 0.05 이하일 때 차이가 있다고 판정한다.
• 위의 경우는 통계량이 자유도의 2배보다 크며, pvalue가 0.05보다 작으므로 차이가 있다고 할 수 있다.

이변량 탐색 : 숫자 -> 범주

요인 x가 숫자, 목표 y가 범주형 변수일 때 데이터를 탐색하는 방법이다.

이 경우, 다른 유형과 달리 명확히 수치화해서 검정하는 방법이 없다.
(이후 배울 로지스틱 회귀를 사용한 방법이 있긴 하다)

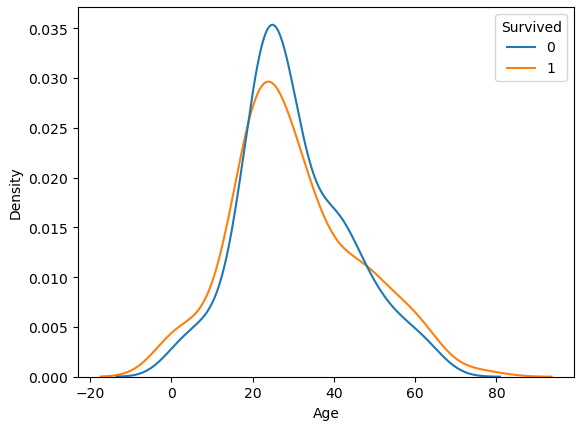
시각화 : kdeplot

• 단변량 범주형 변수 분석에 쓰였던 kdeplot과 hue 옵션을 이용해 시각화 할 수 있다.

• 문법 : sns.kdeplot(x=숫자형 x변수, data=데이터, hue=범주형 y변수, common_norm=False)

  • hue 옵션을 통해 범주별로 그래프를 그릴 수 있다.
  • common_norm은 각각의 그래프가 모두 넓이 1을 갖게 해주는 옵션이다.

• 해석 : 범주 간 선이 교차되는 점을 중심으로 해석한다.

  • 약 20세 이하 구간 : 20세 이하의 승객들이 생존하는 비율이 증가한다.
  • 약 50세 이상 구간 : 50세 이상 구간에서 승객들이 생존하는 비율이 증가한다.

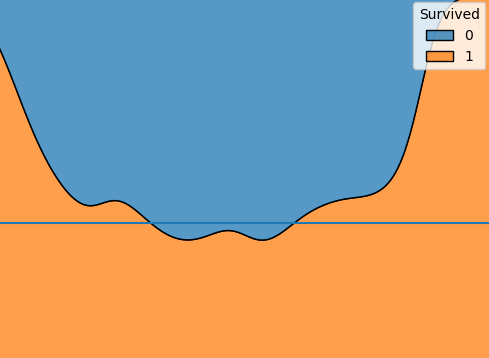
• 문법 : sns.kdeplot(x=숫자형 x변수, data=데이터, hue=범주형 y변수, multiple='fill')
  • plt.axhline을 통해 평균선을 별도로 추가해주었다.
• 해석 : 평균선을 중심으로 해석한다.

소감

• 실습위주로 진행되었던 수업으로, 그간 배웠던 다양한 시각화 Tool을 다루면서 익숙해 질 수 있었다.

• 강사님의 관점과 다른 에이블러분들의 관점을 보며 그래프를 해석하는 여러가지 관점을 알게된 것 같다. 혼자서 그래프를 잡고 끙끙대는 것 보다, 다같이 머리를 맞대는 것이 새로운 인사이트를 얻을 수 있는 좋은 방법이 아닐까?