오늘 배운 것

가설 검정

우리가 과학자라고 가정해보자

• 기존의 발견이나 과학적 결과를 뛰어 넘는 새로운 연구 진행 -> 가설 수립
  • 실험을 통해 결과 데이터를 수집
  • 수집한 데이터를 토대로 나의 가설이 맞다는 것을 입증
• 기존 결과에 근거한 데이터에 비해 수집한 데이터가 얼마나 차이가 나는가? -> 가설 검정

귀무가설과 대립가설

• 귀무가설 : X에 따라 Y는 차이가 없다. / X와 Y는 관련이 없다.

• 대립가설 : X에 따라 Y는 차이가 있다. / X와 Y는 관련이 있다.

  • 내가 세운 가설, 새로운 가설

통계적 검정

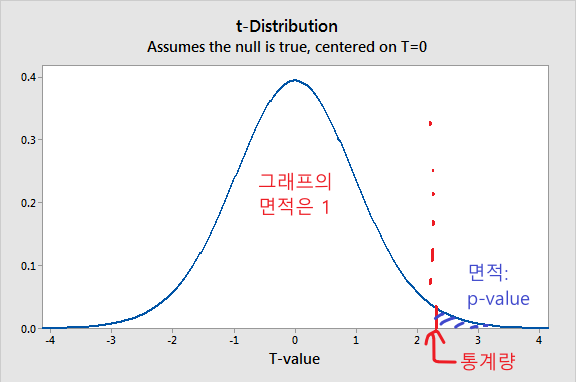
• 표본의 차이를 통해 모집단이 차이가 있음을 검정하고 싶을 때 분포를 이용한다.

• 차이가 있고 없고를 판단할 때는 양측검정, 큰지 작은지를 확인할 때는 단측 검정을 한다. (위 그림은 단측검정)

• p-value는 사실 귀무가설이 맞는데, 대립가설이 맞다고 잘 못 판단할 확률을 나타낸다.
  유의 수준이라고도 하며, 보통 0.05를 기준으로 차이가 있다고 판정한다.

표본평균과 모평균

전국 고등학생의 키 평균을 알고 싶다고 가정하자.

• 모평균 : 전국 남자 고등학생의 평균 키
• 표본평균 : 남자 고등학생 중 무작위 50명의 학생을 뽑아 계산한 평균

• 모평균은 고정된 하나의 값이다.
• 표본평균은 모평균보다 일치할수도, 더 크거나 작을수도 있는 추정치이며 일종의 분포를 갖는다.

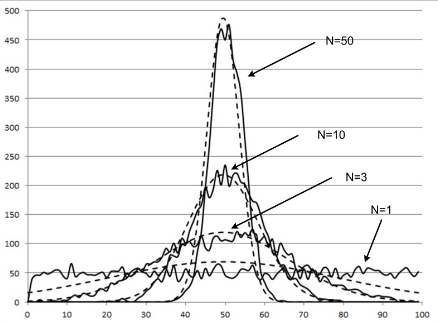
중심극한정리

• 무작위 50명을 뽑는 것을 반복하면 얻어지는 평균값들로 분포를 그릴 수 있다.

• 이 때 표본의 크기(n)가 클 수록 정규분포에 가까워지고, 정규분포 모양이 중심에 가까워지는 현상이 발생한다. -> 중심극한정리

표준오차 (Standard Error)

• 모평균과 표본평균의 차이는 오차라고 한다.

• 표본평균의 분포에서 표준편차를 바로 표준 오차라고한다.

  • 즉 표본의 크기(n)가 커질수록 표준오차는 줄어든다.

95% 신뢰구간

• 95% 신뢰구간이란, 표본평균으로 모평균을 추정할 때, 신뢰구간안에 모평균이 포함될 확률이 95%가 되는 구간이다.

• 더 정확히 말하면, 표본을 100번 뽑아 평균과 95% 신뢰구간을 구했을 때, 그 중 95번은 모평균이 신뢰구간 안에 들어간다는 뜻이다.

• 신뢰구간 계산 : X - 1.96 * SE ≤ 신뢰구간 ≤ X + 1.96 * SE

  • X : 표본 평균
  • SE : 표준 오차
  • 계산 편의성을 위해 1.96대신 2를 쓰기도 한다.