오늘 배운 것

회귀 모델 성능 평가

• 회귀 모델이 완전 정확한 값을 예측하기는 사실상 어려움
• 예측값과 실제값 사이에 오차가 반드시 존재 -> 오차가 적을수록 좋은 모델이다
• 회귀 모델의 평가는 오차를 바탕으로 함

기호

• y : 실제값

  • 모델에게 알려주지 않는 데이터의 실제 값 (정답)

• ŷ (y hat) : 예측값

  • 머신러닝 알고리즘을 통해 우리가 새롭게 예측한 값

• ȳ (y bar) : 평균

  • 이미 알고있는 기존에 예측한 값

• 평균 역시 가장 단순한 형태의 예측값으로서, 머신러닝을 통해 얻은 예측값의 오차가 최소한 평균보다는 적어야 한다. (일종의 판단 기준이 됨)

오차 평균

오차 평균은 오차를 대표하는 하나의 값이다.
작을 수록 좋은 성능을 냄을 뜻한다.

모델의 오차 한계는 바로 평균값의 오차 평균이다.

1. Sum Squared Error (SE, SSE), 오차 제곱합

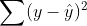
2. Mean Squared Error (MSE)

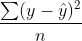
• 오차 제곱합을 데이터의 수로 나눈 것
• 제곱이 된 값이기 때문에 이대로 사용하지는 않는다.

3. Root Mean Squared Error (RMSE)

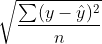
• MSE에 루트를 씌운 것으로 실무에서 가장 널리 쓰이는 오차 평균이다.

4. Mean Absolute Error (MAE)

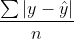
• 제곱합 대신 절대값의 합을 이용한 오차 평균이다.
• 모델의 성능을 평가할 때 사용되는 값중 하나이다.

5. Mean Absolute Percentage Error (MAPE)

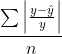
• 각 오차를 실제값 대비 비율로 나타내어, 이들의 평균을 낸 수치이다.

결정계수 (R-Squared)

오차를 보는 관점

• SST (Sum Squared Total) : 평균과 실제값 사이의 오차로, 모델에 허용된 한계 오차를 뜻한다.

• SSE (Sum Squared Error) : 평균과 예측값 사이의 오차로, 회귀식으로 잡아내지 못한 오차를 뜻한다.

• SSR (Sum Squared Regression) : SST- SSE의 값으로 전체 오차 중 회귀식이 잡아낸 오차를 말한다.

SST = SSE + SSR로 나타낼 수 있으며 SSR이 클 수록 모델의 성능이 좋음을 말한다.

결정계수

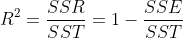
• MSE를 표준화하여 모델의 성능을 잘 나타내는 수치가 바로 결정계수이다.
• SSR / SST를 통해 나타낼 수 있으며, 모델의 예측값이 평균에 비해 얼마나 더 설명을 잘 했는가를 의미한다

• R2 = 1이면 MSE = 0 이란 뜻이며, 모델이 데이터를 완벽히 학습했음을 의미한다.
• R2 = 0.4면 평균에 비해 40% 더 실제값을 잘 설명한다는 의미이다.
• R2가 음수이면 평균보다 예측을 잘 못했다는 의미로, 해당 모델을 폐기해야한다.

분류 모델 성능 평가

• 분류 모델은 명확한 정답이 존재한다. (예측값이 실제값과 동일한가? 동일하지 않은가?)
• 예측값이 실제값과 일치하는 비율이 높을 수록 성능이 높다고 할 수 있다.
• 즉, 정확도로 모델의 성능을 평가한다.

정확도

Simple guide to confusion matrix terminology

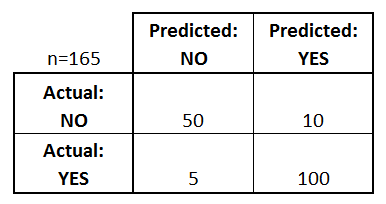
• Accuracy(정확도) : 실제값을 정확히 예측한 비율
  • 위의 그림에서 Accuracy = 150 / 165

• Precision(정밀도) : Yes(1)라고 예측한 것 중에서 정말로 Yes인 비율
  • 위의 그림에서 Precision = 100 / 110

• Recall(재현율) 또는 Sensitivity(민감도) : 실제값이 Yes일 경우 Yes라고 예측한 비율
  • 위의 그림에서 Recall = 100 / 105

• Specificity(특이도) : 특별히 No에서 No라고 예측한 Recall을 특이도라고도 한다.
  • 위의 그림에서 Specificity = 50 / 55

Precision, Recall이 필요한 이유

• Yes일 확률이 95%, No일 확률이 5%라고 했을 때, 예측을 전부 Yes로 해버리면 Accuracy가 95%로 매우 높아보이게 된다.
• 하지만 precision이나 recall로 확인하면 실제값이 No일 때 No로 예측한 비율이 0이므로 예측을 잘 못한 것을 알 수 있다.

• 이렇게 Accuracy만으로는 모델의 정확도를 나타낼 수 없기에 함께 사용한다.
• 일반적으로 Recall을 더 민감하게 본다.
  

혼동 행렬(Confusion Matrix)

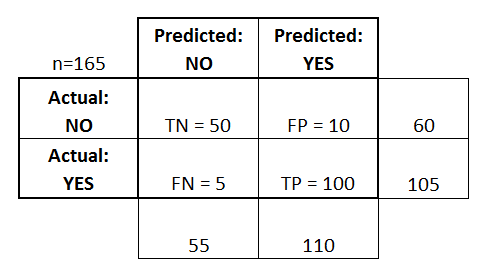
• 예측값이 맞았냐/아니냐 -> True/False
• 양성(1, Yes)이냐/음성(0, No)이냐 -> Positive/Negative

• 이와 같이 분류 문제의 예측 결과를 나타낸 행렬을 혼동 행렬이라 한다.
• 항상 왼쪽위부터 대각선으로 뻗어가는 수치가 정답을 의미한다.

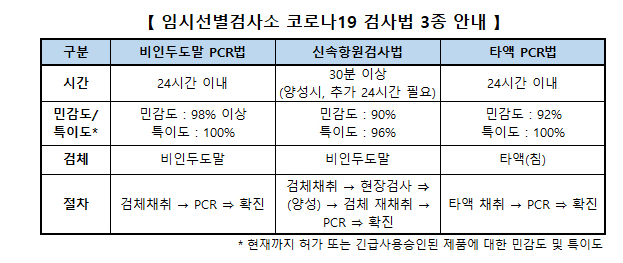
민감도 98% -> 확진자를 확진자라고 판단할 확률이 98% -> 확진자 검사 결과가 음성일 확률 2%
특이도 100% -> 확진자가 아닐 경우 검사 결과가 음성일 확률 100%

즉 음성 판정을 받아도, 양성인데 음성으로 진단됐을 2%의 확률이 있다.
양성 판정을 받으면 100% 코로나 환자이다.

F-1 Score

• Precision과 Recall의 조화 평균을 말한다.
• 조화 평균은 보수적인 평균으로, 한쪽이 크고 한쪽이 작다면 F1-Score가 작은쪽으로 치우친다.
  • 극단적인 값에 덜 민감함
• Precision과 Recall은 분자가 같고 분모가 다른 경우인데, 이렇게 분자가 같고 분모가 다른 값 사이에서는 조화평균이 더 정확하다 할 수 있다.

Classification report

• 혼동행렬의 통계량을 한번에 출력해주는 보고서

• macro avg : 0, 1 통계량의 평균
• weighted avg : 0, 1 통계량의 가중치 평균
  • 0의 데이터가 200개, 1의 데이터가 10이면 평균 계산 시 200 : 10의 가중치가 부여됨
• support : 각 범주값에 해당하는 데이터 양

기본 알고리즘 - 선형회귀(Linear Regression)

• 선형회귀는 데이터의 형태를 설명하는 최선의 직선을 긋는 것이다.
• 최선의 직선은 직선과 실제값의 오차가 제일 작은 직선을 말한다.
• MSE가 최소가 되는 직선의 기울기(가중치)와 편향(절편)을 결정하는 것이 바로 회귀 분석이다.

단순 회귀

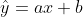
• 독립변수 1개와 종속변수 1개가 일대일 대응 관계를 갖는 선형 회귀
• 이차원 그래프에 표현할 수 있어 시각화가 쉽다.

다중 회귀

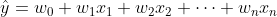
• 여러 독립변수가 종속변수에 영향을 미치는 선형회귀
• 시각화가 어렵다.

회귀 계수

• 직선을 구성하는 기울기와 편향을 회귀 계수라 한다.
• 선형회귀 모델의 속성값을 통해 쉽게 확인할 수 있다.
  • model.coef_ : 가중치
  • model.intercept_ : 편향

vif (varience inflation factors)

• vif는 분산 팽창 요인이라는 뜻으로, 변수 간 공선성의 크기를 나타내는 수치이다.
• vif를 계산할 때는 target 변수를 제거한 상태로, featurn 중 하나를 y로 선택하여 회귀 분석을 진행한다.

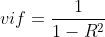
• R2 score 값이 클수록 vif도 증가하며, 일반적으로 10보다 크면 공선성이 큰 것으로 보아 변수 제거를 고려한다.
• 주의 사항 : vif를 할 때는 반드시 정규화를 해야한다.
  범위가 작은 값이 y로 선택 될 경우 대부분의 경우 vif가 높게 나오기 때문에 중요한 데이터를 제거하게 될 수 있기 때문에, 범위를 정규화해야 한다.

오늘의 실습

• sklearn.metrics 모듈의 평가 분석 관련 함수를 호출하여 직접 다양한 평가 지표를 계산하였다.

• 혼동 행렬을 직접 출력하고, sns.heatmap() 을 이용하여 시각화 하였다.

• matplotlib.pyplot 모듈을 이용해 산점도와 회귀 직선을 직접 그려 시각화 하였다.