오늘 배운 것
- 기본 알고리즘 -> 성능은 다소 떨어지지만 설명이 쉬움
- Linear Regression : 어제 배움
- K-Nearest Neighbor (KNN)
- Decision Tree
K-Nearest Neighbor (KNN)
원리
- 새로 데이터가 주어지면, 학습한 데이터에서 k개까지 최근접 이웃을 찾아 주어진 데이터를 분류 또는 예측한다.
- 분류 : k개의 이웃 중 비율(확률)이 더 높은 값으로 분류된다.
- 회귀 : k개의 이웃의 평균을 이용한다.
- 회귀와 분류 모두에 사용할 수 있는 매우 간단한 지도학습 알고리즘
- 이해하기 쉽지만 연산속도가 느리다는 단점이 존재
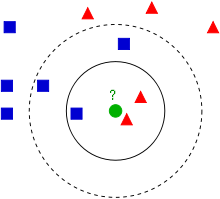
k값의 중요성
- 위 그림에서 k=3일 경우 ○는 빨간색 삼각형으로 분류된다. (1:2)
- k=5일 경우 ○는 파란색 네모로 분류된다. (3:2)
- 즉 k값에 따라 예측값이 크게 변하며, 적절한 k를 찾는 것이 KNN 튜닝의 핵심이다.
- 일반적으로
- k=1은 너무 편향된 정보이므로 되도록 사용하지 않음
- k값이 짝수일 경우 과반수 값이 없는 경우가 발생하므로 잘 사용하지 않음
- 회귀문제에서 k값이 데이터 수와 같다면 모든 예측값은 평균이 된다.
- 분류문제에서 k값이 데이터 수와 같다면 모든 예측값은 최빈값이 된다.
k값이 클수록 모델은 단순해진다.(복잡성 측면), 반대로 작을수록 복잡해진다.
모델이 복잡하면 Overfitting의 가능성도 증가하므로 적절한 k값을 찾아야 한다.
KNN에서 이웃의 거리 구하기
크게 두 가지 거리가 사용된다.
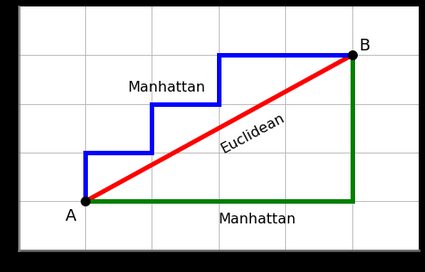
- 유클리드 거리 : 피타고라스 방정식을 이용해서 구할 수 있는 거리
- 차원에 상관없이 모든 차원에 대한 제곱합을 루트로 씌우면 유클리드 거리를 구할 수 있다. (시각화는 불가능)
- 맨해튼 거리 : 대각선 이동 없이 축방향으로만 이동했을 때의 거리
- 맨해튼 거리는 유클리드 거리보다 항상 같거나 길다.
KNN에서 Scaling의 중요성
- KNN은 거리를 바탕으로 이웃을 판정하기 때문에 정규화가 매우 중요하다.
- 범위가 0~1인 변수A와 0~50000인 변수B가 있을 때, A는 아무리 높은 비율로 변해도 거리변화가 없지만, B는 약간만 값이 변해도 거리가 엄청 크게 증가한다.
- 즉 scaling 없이 A와 B를 그대로 사용하면 A쪽에 있는 데이터만 이웃으로 선택될 가능성이 크다
Scaling 방법
1. Normalization
- 모든 데이터의 값을 일정 범위를 갖게 하는 것
- 다양한 방법이 있지만 이번 과정에서는 모든 데이터를 0~1 범위로 변환하는 MinMaxScaler를 사용한다.

- x가 최솟값일 경우 분자가 0이되어 값이 0이 됨
- x가 최대값일 경우 분자와 분모가 동일해져 값이 1이 됨
2. Standardization
- 데이터 값을 평균 0, 표준편차 1의 분포를 갖도록 변환한다.
Scaling 시 주의점
- 한번 스케일링을 하면 더이상 시각화나, 통계량 등에서 인간이 할 수 있는 분석 방법이 거의 없어진다. 때문에 모든 분석을 끝내고 모델링 직전에 스케일링을 진행하자.
Decision Tree (의사결정 트리)

- 특정 변수에 대한 의사결정 규칙을 트리 형태로 분류해 나간다.
- 핵심 : 가장 중요한(의미있는) 질문이 무엇인가?
- 분류와 회귀에 모두 사용할 수 있는 알고리즘이다.
장점
- 분석 과정을 시각화하여 쉽게 눈으로 확인할 수 있다.
- 인간의 의사결정 과정과 비슷하며, 직관적이라 설명이 쉽다. (화이트박스 모델)
- 다만 트리의 깊이가 너무 깊어질 경우 과적합으로 실제 모델성능이 떨어지기 쉽다.
- 트리 깊이를 제한하는 것이 튜닝의 핵심이 된다.
해석
위의 그림을 기준으로 한다.
Rank <= 6.5: True, False로 분기를 나누는 조건gini: gini 불순도를 나타내며, 변수 선택의 기준samples: 현재 노드에 있는 샘플 수value: 현재 샘플의 분포
분류와 회귀
- 분류 : 불순도를 기준으로 가장 불순도를 낮출 수 있는 클래스를 선택
- 의사결정 시 가장 확률이 높은 클래스를 선택
- 회귀 : MSE를 기준으로 MSE를 최소화 할 수 있는 클래스를 선택
- 의사결정 시 샘플들의 평균 등으로 판단
불순도
- 분류문제에서 서로 다른 label이 얼마나 섞여있는 지를 나타내는 수치
- 지니 불순도(Gini impurity)와 엔트로피(Entropy)로 나타낼 수 있다.
지니 불순도

예시 : 전체 10개의 데이터 중 A, B 두가지의 클래스가 각각 5개씩 존재할 경우
즉 binary에서 가장 높은 불순도는 0.5이다. (클래스 수에 따라 달라짐)
트리에서의 변수 선택
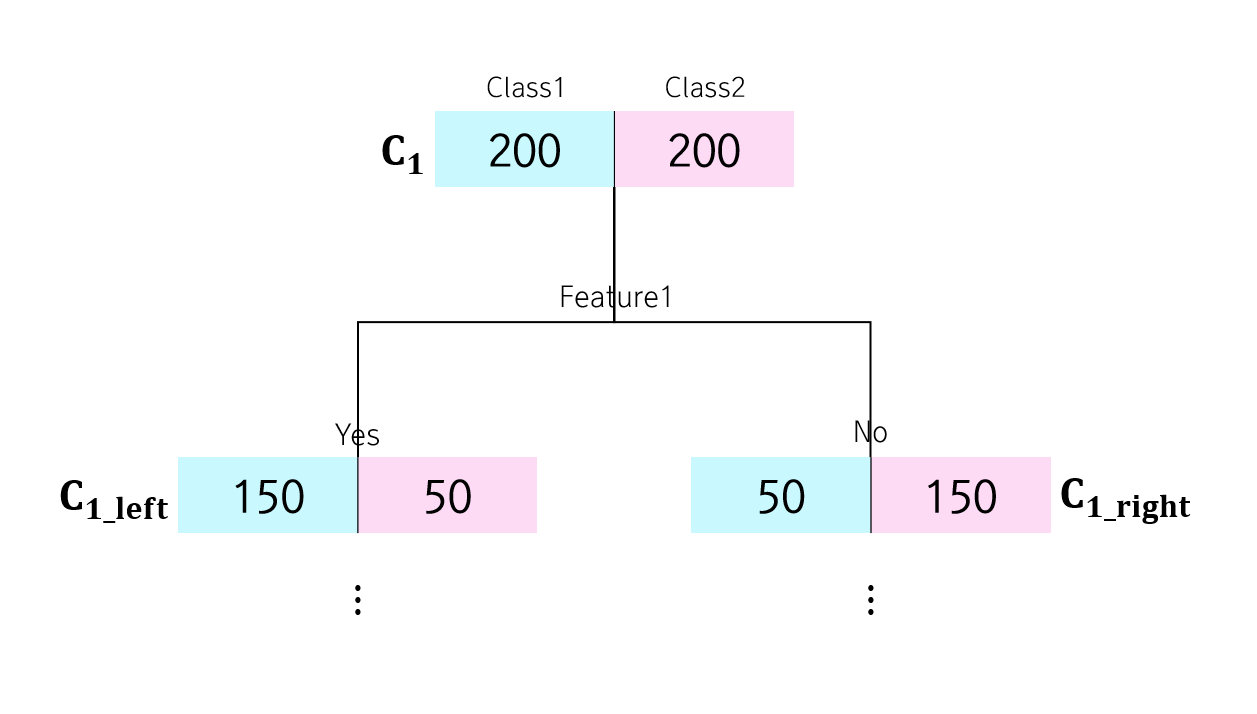
- 부모노드에서 불순도는 0.5임을 알 수 있다.
- 자식노드의 불순도는 각각 0.375, 0.375인데, 이들의 가중치 평균 역시 0.375이다.
- 여기서 0.5 - 0.375 = 0.125만큼 지니 불순도가 감소했음을 알 수 있다. -> 정보 이득(Imformation Gain)
- Decision Tree는 바로 정보 이득이 가장 큰 변수를 최우선으로 선택하여 분할한다.
- 정보이득이 같은 변수가 있다면, 랜덤으로 선택한다.
- 변수의 개수가 너무 많다면 연산량이 늘어나 시간이 오래걸린다는 단점이 있는데, 하이퍼파라미터를 통해 변수 선택수를 제한할 수 있다. (마찬가지로 랜덤 선택)
Decision Tree의 하이퍼파라미터
- 하이퍼파라미터(Hyperparameter)는 알고리즘에 적용되는 파라미터 중 사용자가 직접 선택할 수 있는 파라미터를 의미한다.
- max_depth : 트리의 최대 깊이 (default = None)
- min_samples_leaf : 리프 노드가 될 수 있는 최소한의 샘플 수 (default = 1)
- 리프 노드 : 해당 가지의 가장 마지막 노드
- 만약 분할 시 자식 노드 중 한쪽이라도 min_samples_leaf보다 적은 샘플을 갖게 된다면 더이상 분기를 하지 않는다.
- min_samples_split : 노드를 분할하기 위한 최소한의 샘플 수 (default = 2)
- 만약 현재 노드의 샘플 수가 min_samples_split보다 작다면 더이상 분기를하지 않는다.
- max_feature : 분기를 위해 선택할 변수(feature)의 수
- max_leaf_node : 리프 노드의 최대 개수
실습
- KNN 알고리즘을 이용해 분류 문제에 대한 모델링 실습을 했다.
- n_neighbors 하이퍼파라미터를 통해 k값을 조절하면서 accuracy, recall, precision 등 통계량의 변화를 확인하였다.
- MinMaxScaler 클래스를 이용한 정규화 및 직접 공식을 사용한 정규화를 실습하였다.
- 실전 데이터의 대부분은 0과 1의 비율이 맞지 않는 불균형 클래스이며, 이 경우 recall score가 낮게 나와도 훌륭한 성능으로 판단할 수 있다는 것을 알게 되었다.
정규화 시 주의사항
- 미래데이터(test data)는 현재에 절대 영향을 줄 수 없으므로 정규화 시 최소값, 최대값은 train_data만을 기준으로 사용해야 한다.
- 평가데이터(x_test)의 정규화 역시 train_data를 기준으로 해야한다. train data의 '2'와 test_data의 '2'는 동일함을 보장해야 하는데, train data와 test data의 최소/최대값이 서로 다른다면 정규화 후 값이 달라지기 때문이다.
- Decision Tree 알고리즘을 이용해 분류 문제에 대한 모데링 실습을 했다.
- max_depth 하이퍼파라미터를 통해 트리의 깊이를 제한해가며 성능 점수의 변화를 확인하였다.
- graphviz를 이용하여 트리를 시각화 및 분석하였다.