오늘 배운 것

Logistic Regression

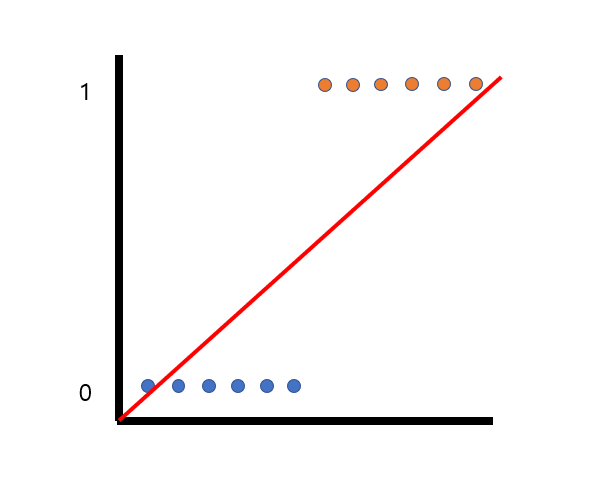
• 사실 회귀선으로 분류 문제를 풀 수 있다.
  • 그림과 같이 직선을 그어서 확률로 판단하면 파란색은 0, 주황색은 1로 분류할 수 있다.
• 그러나 회귀 직선에서 문제점은 직선이 0~1의 확률 범위가 아니라, 음의 무한대 및 양의 무한대를 향한다는 것이다.
• 이를 해결하기 위해 로지스틱 함수(sigmoid)를 사용한 것이 바로 Logistic Regression 알고리즘이다.
• Linear Regression을 기반으로 하기 때문에, 변수의 수가 늘어나면 복잡성도 늘어난다는 특징이 있다.

로지스틱 함수 (시그모이드 함수)

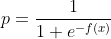
• 데이터 값을 확률값으로 변환하는 함수이다.

• f(x) 값이 무한대로 커지면 e는 0으로 수렴 -> p값은 1로 수렴
• f(x) 값이 무한대로 작아지면 e는 무한대로 수렴 -> p값은 0으로 수렴
• 즉 f(x)는 (0, 1)의 확률 범위를 갖게 된다.

여러개 클래스의 분류

• 0과 1의 binary가 아니라 클래스가 여러가지인 경우, 각각의 클래스에 대한 확률을 구하여 가장 높은 것을 선택한다.
• 이때 softmax 함수란 것이 사용되는데, 자세한 것은 딥러닝을 다룰 때 배울 것이다.

Support Vector Machine (SVM)

• 회귀와 분류 모두 가능한데, 여기서는 분류 관점인 SVC를 바탕으로 설명한다.

Support Vector Machine

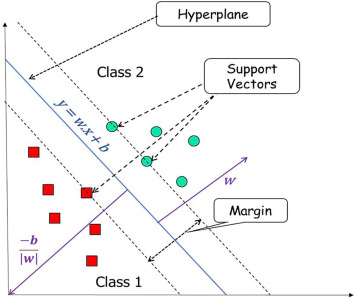
• 분류를 위한 기준선을 찾는 알고리즘이다
• 거리 기반의 알고리즘으로, KNN과 동일하게 정규화 작업이 필요하다.

용어

• Decision Bounday(결정 경계) : 클래스를 분류하는 경계선

• Vectors (벡터) : 2차원 공간상에 나타난 데이터 포인트

• Support Vectors(서포트 벡터) : 벡터들 중 결정 경계와 가장 가까운 데이터 포인트

• Margin (마진) : 서포트 벡터와 결정 경계 사이의 거리

  • 마진을 최대로하는 결정 경계를 찾는 것이 SVM의 목표이다.
  • 마진을 크게 잡을수록 학습데이터에 대해 에러가 발생할 확률이 높지만, 새로운 데이터에 대해 안정적으로 분류할 가능성이 높다.

SVM의 하이퍼파라미터

C(cost)

• SVM알고리즘은 데이터가 마진을 넘어서거나 잘못 분류된 데이터에 대해 에러로 간주하고 패널티를 부과하는데 이것이 비용이다.
  • cost값을 높게 잡을 수록 SVM은 에러에 대해 더 큰 비용을 부과하여 좁은 마진을 갖는다.
    -> 학습데이터에 대한 성능 상승, 지나치면 overfitting 발생 가능성
  • cost값을 낮게 잡을 수록 SVM은 에러에 관대하여 더 넓은 마진을 갖는다.
    -> 실제 성능이 안정적일 가능성이 상승, 지나치면 underfitting 발생 가능성
• default 값은 1이다.

kernel

• 결정 경계의 선형을 나타내는 파라미터이다.
• 선형(linear), 등고선형(rbf), poly 등이 있다.

gamma

• 결정 경계의 곡률을 의미한다.
• gamma 값이 클 수록 곡률 반경이 작아지며 결정 경계가 더 급하고 자세한 수준의 curve를 갖는다.

적절한 C와 gamma를 찾아야 한다.

모델의 복잡성

• 모델이 복잡하다는 것은?
  • 학습 데이터에 너무 치중한 나머지, 실제 평가 시 성능이 좋지 않은 것을 의미
  • 즉 과대적합의 위험이 높다는 것을 의미

모델이 복잡한 경우

1. Linear Regression, Logistic Regression : 변수가 많을 수록
2. KNN : k값(n_neighbors)이 작을수록
3. Decision Tree : max_depth가 클 수록
4. SVM : C가 클수록, gamma가 클 수록

K-Fold Cross Validation (K-분할 교차검증)

Random Split의 문제

• 실제 테스트에 들어가기 전에 train data를 바탕으로 모델의 예상 성능을 도출하고, 최적의 모델 및 하이퍼파라미터를 찾아야 한다.
• 이를 위해 validation data(검증용 데이터)를 사용하는데, 그냥 무작위 선정을 하면 같은 데이터가 여러번 선정되거나, 선정되지 않는 데이터가 존재할 수 있다. -> 비효율
• 모든 데이터를 단 한 번씩만 검증용 데이터로 사용하는 효율적이고 체계적인 방법이 필요한데, 이것이 바로 K-Fold Cross Validation이다.

K-분할 교차검증의 개념

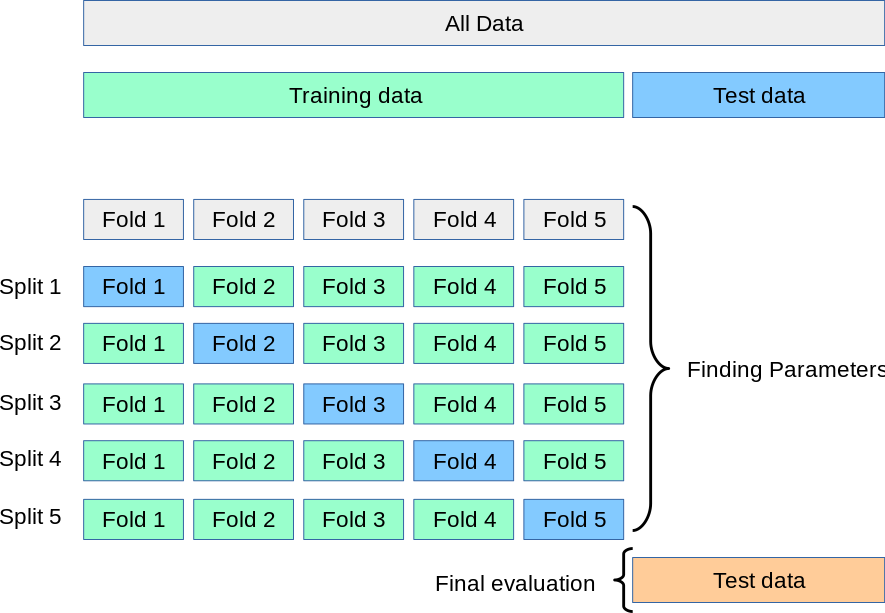
sklearn - Cross-validation: evaluating estimator performance

• 데이터를 k등분으로 나누어, 모든 데이터를 평가에 1번, 학습에 k-1번 사용하도록 하는 알고리즘
• 최초 1회에 데이터를 섞은 후, 이를 고정한 채 k값에 맞도록 분할하여 교차 검증한다.
• cv 옵션을 통해 k값을 설정할 수 있다.
  • cv=10이면 검증용 데이터의 비율을 1:9로 하여 총 10번 교차검증한다.
  • cv의 기본값은 5이다.
  • cv는 적어도 2 이상이어야 한다.

장단점

• 장점
  • 모든 데이터를 학습과 평가에 사용 가능
  • 반복 학습과 평가를 통한 정확도 향상
  • 결과적으로 모든 train data를 온전히 사용하므로, 데이터 부족으로 인한 underfitting 문제 방지
  • 검증용 데이터의 편향 발생을 방지
  • 좀 더 일반화된 모델을 만들 수 있음
• 단점
  • 반복 횟수가 많아서 많은 시간이 소요됨 (특히 하이퍼파라미터와 조합 시)

하이퍼파라미터 튜닝

Hyperparameter

• 알고리즘을 사용하여 모델링할 때 최적화를 위해 사용자가 조절할 수 있는 옵션
• 튜닝하는 방법에 정답은 없다. (지식과 경험 + 다양한 시도)
• 튜닝을 위한 방법에는 Grid Search와 Random Search가 있다.

Grid Search

• 각 하이퍼파라미터의 범위를 정한 뒤, 해당 범위 모두를 테스트하며 성능 정보를 수집한다.
• 가장 성능이 좋았던 하이퍼파라미터 조합을 최종 선택하여 자동으로 모델링 및 평가를 진행한다.
• 도출된 모델을 바탕으로 예측 및 평가 과정을 진행하면 된다.

• 장점 : 모든 범위를 탐색하므로 높은 신뢰도를 갖는 최적의 파라미터 값 선택 가능
• 단점 : n값이 크다면 상당히 많은 시간이 소요된다.
  • 파라미터 종류가 n, 각 범위가 m, cv값이 k라면 n * m * k회의 반복을 수행해야 함

Random Search

• 각 하이퍼파라미터의 범위를 정한 뒤, 무작위로 m개를 골라 테스트하며 성능 정보를 수집한다.
• 이후로는 Grid Serach와 마찬가지로 가장 성능이 좋았던 하이퍼파라미터 조합을 최종 선택하여 자동으로 모델링 및 평가를 진행한다.
• m는 n_iter 옵션을 통해 사용자가 정할 수 있다.

• 장점 : Grid Search보다 더 적은 시간과 자원을 소모한다.
• 단점 : 선택되지 못한 값 중 더 좋은 성능을 보이는 값을 놓칠 수 있다.

실습

• SVM의 SVC, SVR 알고리즘을 이용해 각각 분류문제와 회귀문제 모델링 실습을 했다.

  • x가 1종류인 이차원 데이터셋을 통해 시각화를 하며 kernel마다 어떤 선형을 갖는지 확인했다.
  • cost값에 따라 마진의 크기가 어떻게 변하는지 확인하였다.

• 각 모델에 대해 K-분할 교차 검증을 하며 각 데이터 셋에 대해 가장 높은 성능을 가질 것으로 예측되는 모델을 선택했다.

  • cv_score를 결과에 받아 각 모델을 비교하는 시각화를 진행했다.
  • cross_validate 함수를 통해 동시의 여러종류의 스코어링을 진행하였다.

• KNN, SVM과 같은 거리 기반의 알고리즘은 반드시 데이터 정규화가 필요하다는 것에 주의해야 한다.