오늘 배운 것
ML, DL 복습
Scaling의 오해
- 스케일링의 결과로 데이터의 분포를 정규분포로 한다는 것으로 잘못 알고있는 경우가 많은데, 이는 오해다.
- 스케일링은 데이터의 분포를 변화시키지 않는다.
- 스케일링은 데이터의 분포를 유지한채로, 범위를 축소시키는 것이다.
- 서로다른 범위 때문에 거리기반 알고리즘에서 범위가 큰 변수에 더 큰 영향을 받는 것을 예방
- 거리기반이 아닌 Random Forest, XGBoost 등의 알고리즘에서는 스케일링이 별 영향을 ㅜ지 않는다.
Grid Search 시각화
- Grid Search를 수행한 후에는 꼭 시각화를 해야한다.
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import GridSearchCV
model = DecisionTreeRegressor()
param_grid = {
'max_depth' : range(3,40)
}
grid = GridSearchCV(model, param_grid=param_grid, cv=5, verbose=2)
grid_result = grid.fit(x_train, y_train)- Decision Tree 모델을 만들어 max_depth 하이퍼파라미터 최적화를 위해 Grid Search를 진행하였다.
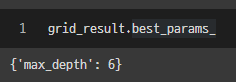
- 가장 좋은 파라미터가 무엇인지 찍어보았더니 max_depth가 6일 때임을 알려준다.
- 하지만 이를 그대로 믿을 수 있을까?
# 튜닝 과정 로그를 df로 저장
result = pd.DataFrame(grid_result.cv_results_)
# df를 바탕으로 시각화
plt.figure(figsize = (15,8))
sns.lineplot(x='param_max_depth', y='mean_test_score', data = result, marker = 'o')
plt.grid()
plt.show()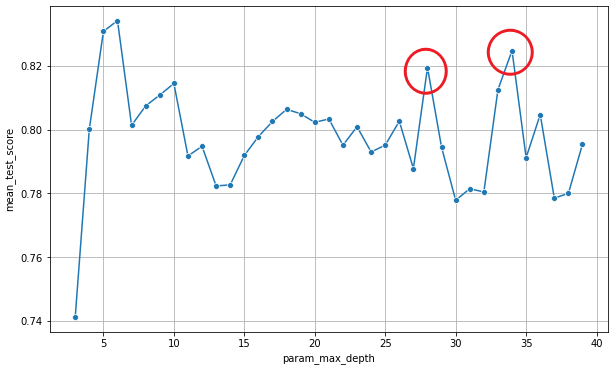
- cv를 찍어보면 max_depth가 커짐에 따라 어느 순간 성능이 증가하지 않거나 하락하는 구간을 맞이하게된다 (elbow curve)
- 그런데 랜덤한 요소로 인해 성능 값이 튈 수도 있는데, 다행히 이번 모델에서는 best params를 잘 찾아 내었지만, 저렇게 튄 값을 최적의 하이퍼파라미터라고 잘못 판단할 수 있다.
- 때문에 Grid Search 결과를 그대로 믿지말고 꼭 시각화하는 과정을 거쳐야 한다.
np.linspace
-
이번에 자잘하게 알게된 numpy함수로 소수값에 대해 range 역할을 한다.
-
np.linspace(0.01, 0.2, 50): [0.01, 0.2] 범위의 값을 일정한 간격으로 50개 생성한다.
n_estimators
- Random Forest, XGBoost 등의 앙상블 알고리즘에서 트리의 개수를 뜻하는 하이퍼파라미터이다.
- 다만 이 트리가 하는 역할은 조금씩 다르다
Random Forest
- RF에서 n_estimators는 트리의 개수를 의미하며, 전체 변수 중 max_features 값 만큼의 랜덤한 변수를 기준으로 사용한다.
- max_features의 기본값은 전체 변수 개수의 제곱근이며, 직접 숫자를 지정하거나 로그를 취하도록 할 수 있다.
- 회귀문제라면 각 트리가 예측한 값의 평균을 내며, 분류문제라면 각 트리가 보팅을 한다.
XGBoost
- XGB에서도 n_estimators는 트리의 개수를 의미하는데 조금 개념이 다르다.
- 먼저 m1의 학습결과로 발생한 오차에 대해 m2가 학습하여 오차를 줄이고, 다시 m2의 오차를 m3가 학습하는 식으로 n_estimators 개수만큼 순차적으로 반복한다.
- 학습한 것을 다음모델에 반영할 정도를 learning_rate 하이퍼파라미터로 결정한다.
model = lr * m1 + lr * m2 + lr * m3 + ...이런식으로 순차적으로 이어진다.
비즈니스를 위한 인공지능
- 우리가 머신러닝, 딥러닝 모델을 만들고 무언가 예측하는 것은 비즈니스 문제를 해결하기 위함이다.
고객이 AI 전문가에게 던지는 두 가지 질문
- 모델이 왜 그렇게 예측했나요? (해석·설명)
- 그 모델은 비즈니스 문제를 해결할 수 있을까요?
금요일 과정까지 이 질문에 대답하는 방법을 배울 것이다.
모델의 해석과 설명
Interpretability (해석)
- Input에 대해 모델은 왜 그런 Output을 예측했는가?
- 선형 모델이라면 선형 회귀식이 여기에 해당 (
y = 2 * x1 - 3 * x2 + 5)
- 선형 모델이라면 선형 회귀식이 여기에 해당 (
- 어떤 변수가 모델에서 가장 중요한가?
- Feature Importance
- 이를 본질적으로 해석 가능한 모델을 Whitebox model이라 한다.
- 선형식을 명확히 도출할 수 있는 Linear Regression, Split 기준을 시각화 가능한 Decision Tree 등이 여기에 해당한다.
- Output이 나온 과정을 본질적으로 해석할 수 없는 모델을 Blackbox model이라 한다.
- 딥러닝이 여기에 해당한다.
Explainability (설명)
- Explainability는 해석을 포함한 개념으로, 여기에 더해 과정의 투명성을 요구한다.
- 즉 모델이 학습한 과정을 단계별로 설명할 수 있어야한다는 개념이다.
- 최근에는 해석과 설명을 혼용해서 사용한다.
Trade-Off 관계
- 설명이 잘되는 알고리즘은 대체로 성능이 낮다. -> Linear Regression, Decision Tree
- 성능이 좋은 알고리즘은 대체로 성능이 어렵다. -> Catboost, Random Forest
모델에 대한 설명
모델에 대한 설명은 결국 모델의 성능이 좋을 때 의미가 있는 것이다.
틀린 답안을 들고 어떻게 풀었는지 분석하는 것은 아무 의미가 없다.
- 모델에서 어떤 feature가 가장 중요할까? -> Feature Importance
- 특정 Feature의 값이 변하면 예측값은 어떻게 변화할까? -> Partial Dependent Plot (PDP)
- 이 데이터(분석단위)는 왜 이렇게 예측되었나? -> Shapley Additive Explanation (SHAP)
변수 중요도
Feature Importance
- 알고리즘 별 내부 규칙에 의해 계산된, 예측에 대한 변수 별 영향도를 측정, 수치화한 값
- Tree 기반 알고리즘에서는 자체적으로 Feature Importance를 제공한다.
트리 기반 알고리즘의 Feature Importance 측정
Mean Decrease Impurity(MDI)
- Information Gain(정보이득) : 트리가 분기했을 때 지니 불순도가 감소하는 정도
- MDI는 각 feature별로 Information Gain의 가중 평균을 계산한 수치이다.
- 여기서 분기하는 노드의 Sample 수가 가중치가 된다.
- 즉 많은 샘플을 분기시키고, 정보이득을 많이 얻은 feature일 수록 MDI가 높다.
Mean Decrease GINI
- Random Forest에서 사용하는 변수 중요도로, estimators로 참여하는 각 트리의 MDI 평균을 구하여 도출한다.
- 각 트리를 직접 뽑아내어 중요도를 구한 뒤, 평균을 내보면 RF 모델이 제공하는 feature importance와 동일한 것을 확인할 수 있다.
부스팅 계열의 Feature Importance 측정
- 대표적으로 XGBoost의 경우 3가지 방법으로 변수 중요도를 제공한다.
1. weight
- 트리가 분리될 때, 기준으로 사용된 횟수의 합으로 중요도를 나타낸다.
plot_importance라는 xgboost 라이브러리 함수를 사용했을 때 기본으로 나오는 값이다.
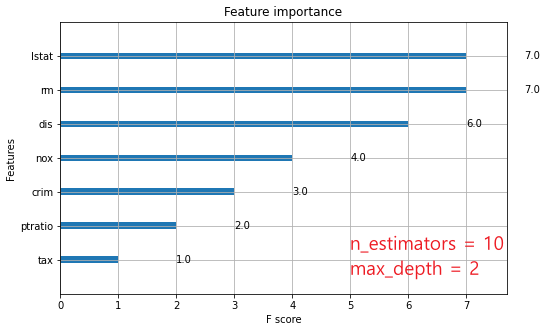
- 위 그림처럼 10개의 트리로 max_depth = 2로 부여하면 각 트리당 3번씩 총 30번의 분기를 하게된다.
때문에 Feature Importance의 합을 구하면 30인 것을 확인할 수 있다.
2. gain
- 각 feature별로 평균 imformation gain을 구한 것이다.
model.feature_imfortances_를 찍었을 때 나온느 기본 값이다.- 매개변수로 total_gain을 전달하면 평균 대신 총합을 사용한다.
3. cover
- 트리가 분기될 때의 샘플 수 평균을 낸 것이다. 트리의 깊이가 얕을 때 자주 선택된 기준일수록 높은 값을 갖는다.
Permutation Feature Importance (PFI)
- 알고리즘에 상관없이 Feature Importance를 구할 수 있는 방법이다.
- 전체 학습데이터에서 Feature 하나를 선택해 무작위로 뒤섞었을 때 model의 성능이 얼마나 감소되었는지를 계산한다.
- 무작위성이 있으므로, K를 지정하여 성능감소를 계산하는과정을 K번 반복하여 평균을 낸 것을 사용한다.
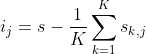
- s : 원래 모델의 점수, s(j) : j변수를 섞었을 때 성능 점수, K : K번 실행
- 해석 : PFI가 클 수록 해당 변수가 중요하다는 의미이다. (모델 성능이 크게 감소했으므로)
단점
- 만약 요인간의 공선성이 존재할 경우, 그 중 하나를 섞어도 모델의 성능에 큰 변화가 없게 된다. 이러한 경우 공선성이 존재하는 요인의 PFI를 정상적으로 구할 수 없다.
함수 및 시각화
- sklearn이 제공하는
permutaion_importance함수를 통해 쉽게 계산 및 시각화가 가능하다.
from sklearn.inspection import permutation_importance
pfi = permutation_importance(model, x_val, y_val, n_repeats=10, scoring='r2')- model : 평가할 모델 (학습이 완료된 상태여야 함)
- x_val, y_val : 평가에 사용할 데이터 (학습에 사용되지 않은 데이터이어야 함)
- n_repeats : 반복 횟수
- scoring : 성능 점수의 기준
- 해당 함수는 pfi 값을 딕셔너리 형태로 반환하고, 딕셔너리에는 각 pfi값 및 평균 pfi값이 들어있기 때문에 쉽게 시각화가 가능하다.
- 학습된 모델, 평가할 데이터만 있으면 어떤 모델에도 적용가능하다. (딥러닝 포함)

